Подготовка к ЕГЭ. Задачи на сплавы. материал для подготовки к егэ (гиа) по алгебре (11 класс) на тему
Прототип Задания B14 (№99576 )
Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава . Ответ дайте в килограммах.
Решение
Пусть x (кг) — масса первого сплава, тогда (x+3) (кг) — масса второго сплава.
Так как первый сплав содержит 10% меди, то в нем 0,1x (кг) меди. Во втором сплаве — 0,4(x+3) (кг) меди.
Масса полученного сплава равна x+x+3 = 2x+3 (кг).
Так как из этих двух сплавов получили третий сплав, содержащий 30% меди, то составим и решим уравнение:
0,1x+0,4(x+3) = 0,3(2x+3),
0,1x+0,4x+1,2 = 0,6x+0,9,
0,6x-0,5x = 1,2-0,9,
Тогда масса третьего сплава равна 2*3+3 = 6+3 = 9.
Прототип Задания B14 (№99575 )
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Решение
x+y = 200. (уравнение 1)
В первом сплаве содержится 10 % никеля, т.е. 0,1x (кг) никеля, а во втором сплаве — 30% никеля, т.е. 0,3y (кг) никеля. Третий сплав содержит 25% никеля, т.е. 0,25*200 = 50 (кг) никеля. Получаем уравнение:
x+3y = 500. (уравнение 2)
x+3y — (x+y) = 500 — 200,
x = 200 — 150 = 50.
Тогда y-x = 150 — 50 = 100 (кг), т.е. масса первого сплава меньше массы второго сплава на 100 кг.
Ответ: 100.
Задание B14 (ЕГЭ 2014 )
Имеется два раствора. Первый содержит 10% соли, второй – 30% соли. Из этих двух растворов получили третий раствор массой 200 кг, содержащий 25% соли. На сколько килограммов масса первого раствора меньше массы второго?
Решение
Пусть x (кг) — масса первого раствора, y (кг) — масса второго раствора. Тогда масса третьего раствора равна
x+y = 200. (уравнение 1)
(уравнение 1)
В первом растворе содержится 10 % соли, т.е. 0,1x (кг) соли, а во втором растворе — 30% соли, т.е. 0,3y (кг) соли. Третий раствор содержит 25% соли, т.е. 0,25*200 = 50 (кг) соли. Получаем уравнение:
Умножим последнее уравнение на 10, получим:
x+3y = 500. (уравнение 2)
Вычтем из уравнения 2 уравнение 1:
x+3y — (x+y) = 500 — 200,
x = 200 — 150 = 50.
Тогда y-x = 150 — 50 = 100 (кг), т.е. масса первого раствора меньше массы второго раствора на 100 кг.
Ответ: 100.
Задание B14 (ЕГЭ 2014 )
Имеется два сплава. Первый содержит 10% никеля, второй 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго сплава?
Решение
Пусть x (кг) — масса первого сплава, y (кг) — масса второго сплава. Тогда масса третьего сплава равна
x+y = 225. (уравнение 1)
В первом сплаве содержится 10 % никеля, т.
0,1x+0,35y = 67,5.
Умножим последнее уравнение на 10, получим:
x+3,5y = 675. (уравнение 2)
Вычтем из уравнения 2 уравнение 1:
x+3,5y — (x+y) = 675 — 225,
x = 225 — 180 = 45.
Тогда y-x = 180 — 45 = 135 (кг), т.е. масса первого сплава меньше массы второго сплава на 135 кг.
Ответ: 135.
Задание B14 (ЕГЭ 2014 )
Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 25 км. Путь из А в В занял у туриста 6 часов, из которых 1 час ушёл на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 1 км/ч. Ответ дайте в км/ч.
Решение
Пусть x (км/ч) — скорость туриста на спуске. Тогда скорость туриста на подъеме равна x-1 (км/ч).
Путь на подъеме занял 6-1 = 5 часов. Составим уравнение:
x = 5 (км/ч) — скорость туриста на спуске.
Задание B14 (ЕГЭ 2014 )
Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 38 км. Путь из А в В занял у туриста 8 часов, из которых 6 часов ушло на спуск. Найдите скорость туриста на спуске , если она больше скорости на подъёме на 5 км/ч. Ответ дайте в км/ч.
Решение
Пусть x (км/ч) — скорость туриста на спуске. Тогда скорость туриста на подъеме равна x-5 (км/ч).
Путь на подъеме занял 8-6 = 2 часа. Составим уравнение:
x = 6 (км/ч) — скорость туриста на спуске.
Прототип задания B14 (№ 99574 )
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 20 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
Имеется два сплава. Первый содержит 15% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 140 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Пусть масса первого сплава а масса второго — Тогда массовое содержание никеля в первом и втором сплавах и соответственно. Из этих двух сплавов получили третий сплав массой 140 кг, содержащий 30% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 70 килограммов.
Ответ : 70.
Ответ: 70
Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 4
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 90 килограммов.
Ответ
: 90.
Ответ: 90
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 25% никеля. Получаем систему уравнений:
Ответ : 45.
Ответ: 45
Классификатор базовой части: Задачи на проценты, сплавы и смеси
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 250 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Пусть масса первого сплава кг, а масса второго — кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно.
Следовательно, масса второго сплава 150 кг. Разность масс — 50 кг.
Ответ : 50.
Ответ: 50
Классификатор базовой части: Задачи на проценты, сплавы и смеси
Имеется два раствора. Первый содержит 10% соли, второй — 30% соли. Из этих двух растворов получили третий раствор массой 200 кг, содержащий 25% соли. На сколько килограммов масса первого раствора была меньше массы второго?
Решение.
Пусть масса первого раствора кг, а масса второго – кг. Тогда массовое содержание соли в первом и втором растворах и , соответственно. Из этих двух растворов получили третий раствор массой 200 кг, содержащий 25% соли. Получаем систему уравнений:
Таким образом, масса первого раствора меньше массы второго на 100 килограммов.
Ответ : 100.
Ответ: 100
Источник: ЕГЭ по математике 05.06.2014. Основная волна. Запад. Вариант 1., ЕГЭ 28.04. 2014 по математике. Досрочный экзамен. Вариант 1.
2014 по математике. Досрочный экзамен. Вариант 1.
Классификатор базовой части: Задачи на проценты, сплавы и смеси
Имеется два сплава. Первый содержит 10% никеля, второй – 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 30% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 135 килограммов.
Ответ : 135.
Ответ: 135
Источник: ЕГЭ по математике 05.06.2014. Основная волна. Восток. Вариант 1.
Классификатор базовой части: Задачи на проценты, сплавы и смеси
Имеется два сплава. Первый сплав содержит 5% меди, второй — 12% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение.
Ответ: 7
Классификатор базовой части: Задачи на проценты, сплавы и смеси
Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение.
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание меди в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав кг, содержащий 10% меди. Получаем систему уравнений:
Тогда масса третьего сплава равна: кг
Ответ: 63.
Ответ: 63
Классификатор базовой части: Задачи на проценты, сплавы и смеси
Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 5 кг.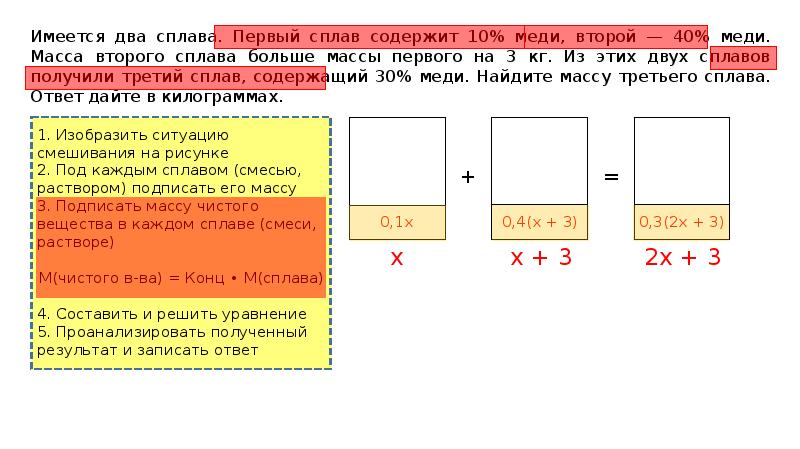 Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение.
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание меди в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав кг, содержащий 10% меди. Получаем систему уравнений:
Тогда масса третьего сплава равна: кг
Ответ: 45.
Ответ: 45
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
прототипа.
Ответ : 100.
Ответ: 120
Имеется два сплава. Первый содержит 5% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Это задание ещё не решено, приводим решение прототипа.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ : 100.
Ответ: 75
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Это задание ещё не решено, приводим решение прототипа.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ : 100.
Ответ: 105
Имеется два сплава. Первый содержит 5% никеля, второй — 20% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 15% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Это задание ещё не решено, приводим решение прототипа.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ : 100.
Ответ: .
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Это задание ещё не решено, приводим решение прототипа.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Получаем систему уравнений:
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ : 100.
Ответ:
Имеется два сплава. Первый содержит 5% никеля, второй — 25% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Это задание ещё не решено, приводим решение прототипа.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ : 100.
Имеется два сплава. Первый содержит 5% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 100 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Первый содержит 5% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 100 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Это задание ещё не решено, приводим решение прототипа.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ : 100.
Ответ: 5
Имеется два сплава. Первый содержит 10% никеля, второй — 25% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Это задание ещё не решено, приводим решение прототипа.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ : 100.
Имеется два сплава. Первый содержит 5% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Это задание ещё не решено, приводим решение прототипа.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ : 100.
Ответ: 125
Имеется два сплава. Первый содержит 5% никеля, второй — 25% никеля. Из этих двух сплавов получили третий сплав массой 100 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Это задание ещё не решено, приводим решение прототипа.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
На сколько килограммов масса первого сплава была меньше массы второго?
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ : 100.
Ответ: 0
Имеется два сплава. Первый содержит 10% никеля, второй — 40% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Это задание ещё не решено, приводим решение прототипа.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ : 100.
Ответ: 0
Имеется два сплава. Первый содержит 5% никеля, второй — 40% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 35% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Это задание ещё не решено, приводим решение прототипа.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Получаем систему уравнений:
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ : 100.
Ответ: 125
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 250 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Это задание ещё не решено, приводим решение прототипа.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ
: 100.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 100 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Решение.
Это задание ещё не решено, приводим решение прототипа.
Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Пусть масса первого сплава кг, а масса второго – кг. Тогда массовое содержание никеля в первом и втором сплавах и , соответственно. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. Получаем систему уравнений:
Таким образом, первый сплав легче второго на 100 килограммов.
Ответ : 100.
Ответ: 00000
Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
На сколько килограммов масса первого сплава была меньше массы второго?
Задачи на сплавы.
1.1. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
2. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
3. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 13% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
4. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Ответ дайте в килограммах.
5. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 8 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
6. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
7. Первый сплав содержит 5% меди, второй — 11% меди. Масса второго сплава больше массы первого на 2 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
8. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 6 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
9. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 5 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Масса второго сплава больше массы первого на 5 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
2.1. Имеется два сплава. Первый сплав содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
2. Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?
3. Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
4. Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?
На сколько килограммов масса первого сплава меньше массы второго?
5. Имеется два сплава. Первый сплав содержит 5% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
6. Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава меньше массы второго?
7. Имеется два сплава. Первый сплав содержит 5% никеля, второй — 20% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 15% никеля. На сколько килограммов масса первого сплава меньше массы второго?
8. Имеется два сплава. Первый сплав содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
9.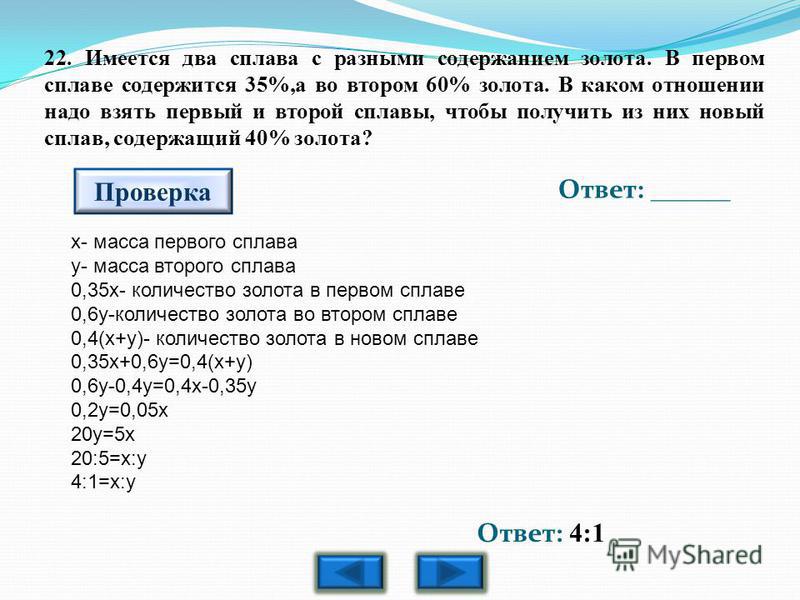 Имеется два сплава. Первый сплав содержит 5% никеля, второй — 25% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Имеется два сплава. Первый сплав содержит 5% никеля, второй — 25% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Задачи на сплавы.
Проценты переводим в десятичную дробь.
Количество вещества = масса сплава на десят. дробь.
1.1.Имеется два сплава. Первый сплав содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Решение.
Масса сплава % содержание Кол-во никеля
1-ый сплав х 10%=0,1 0,1х
2-ой сплав 200-х 30%=0,3 0,3(200-х)=60-0,3х
3-ий сплав 200 25% =0,25 0,25 200=50
Складываем количество никеля 1 и 2 сплавов и приравниваем к количеству 3 сплава.
Уравнение:
0,1x+60-0,3x=50
0,2x=10
X=50 — масса 1-го сплава
Тогда 200-50=150 – масса 2-го сплава
Разница 150-50=100
ОТВЕТ: 100
2. 1.Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
1.Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение.
Масса сплава % содержание Кол-во меди
1-ый сплав x 10%=0,1 0,1x
2-ой сплав x+3 40%=0,4 0,4(x+3)
3-ий сплав 2x+3 30%=0,3 0,3(2x+3)
Уравнение:
0,1x+0,4(x+3)=0,3(2x+3)
0,1x=0,3
Масса 3-го сплава равна 2 3+3=9
ЕГЭ Текстовые задачи | ЕГЭ Текстовые задачи | ||||
1 | Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. | 1 | Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 10 кг. Из этих двух сплавов получили третий сплав, содержащий 12% меди. Найдите массу третьего сплава. Ответ дайте в килограммах | ||
2 | Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго? | 2 | Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 175 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго? | ||
3 | Смешав 45-процентный и 97-процентный растворы кислоты и, добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. | 3 | Смешав 45-процентный и 97-процентный растворы кислоты и, добавив 10 кг чистой воды, получили 62-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси? | ||
4 | В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составит концентрация получившегося раствора? | 4 | В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 5 литров воды. | ||
5 | Имеется два сосуда. Первый содержит 60 кг, а второй — 20 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 30% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 45% кислоты. Сколько процентов кислоты содержится в первом сосуде? | 5 | Имеется два сосуда. Первый содержит 60 кг, а второй — 20 кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 30% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 45% кислоты. Сколько процентов кислоты содержится в первом сосуде? | ||
6 |
| 6 |
| ||
7 | Девять одинаковых рубашек дешевле куртки на 10%. На сколько процентов двенадцать таких же рубашек дороже куртки? | 7 | Девять одинаковых рубашек дешевле куртки на 10%. На сколько процентов двенадцать таких же рубашек дороже куртки? | ||
8 | Семья состоит из мужа, жены и их дочери-студентки. | 8 | Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 66%. Если бы стипендия дочери уменьшилась вчетверо, общий доход семьи сократился бы на 6%. Сколько процентов от общего дохода семьи составляет зарплата жены? | ||
9 | Расстояние между городами A и B равно 390 км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему | 9 | Расстояние между городами A и B равно 390 км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему | ||
10 | Заказ на 247 деталей первый рабочий выполняет на 6 часов быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 6 деталей больше? | 10 | Заказ на 247 деталей первый рабочий выполняет на 6 часов быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 6 деталей больше? | ||
11 | Байдарка в 7:007:00 вышла из пункта А в пункт В, расположенный в 30 км от А. | 11 | Байдарка в 7:007:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа 40 минут, байдарка отправилась назад и вернулась в пункт А в 23:0023:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость байдарки равна 6 км/ч. | ||
12 | Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в город В на 4 часа раньше, чем велосипедист приехал в город А, а встретились они через 1 час 30 минут после выезда. Сколько часов затратил на путь из города В в город А велосипедист? | 12 | Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. | ||
13 |
| 13 |
| ||
14 | Один мастер может выполнить заказ за 30 часов, а другой — за 15 часов. | 14 | Один мастер может выполнить заказ за 30 часов, а другой — за 15 часов. За сколько часов выполнят заказ оба мастера, работая вместе? | ||
15 | Первая труба наполняет резервуар на 13 минут дольше, чем вторая. | 15 | Первая труба наполняет резервуар на 13 минут дольше, чем вторая. | ||
16 | Даша и Маша пропалывают грядку за 12 минут, а одна Маша – за 20 минут. За сколько минут пропалывает грядку одна Даша? | 16 | Даша и Маша пропалывают грядку за 12 минут, а одна Маша – за 20 минут. | ||
17 | Первый и второй насосы наполняют бассейн за 9 минут, второй и третий – за 14 минут, а первый и третий – за 18 минут. За сколько минут этим три насоса заполнят бассейн, работая вместе? | 17 | Первый и второй насосы наполняют бассейн за 9 минут, второй и третий – за 14 минут, а первый и третий – за 18 минут. За сколько минут этим три насоса заполнят бассейн, работая вместе? | ||
18 | Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 9 рабочих, а во второй – 11 рабочих. Через 6 дней после начала работы в первую бригаду перешли 3 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Сколько дней потребовалось на выполнение заказов? | 18 | Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. | ||
19 | Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь – за 18 часов. За сколько часов мальчики покрасят забор, работая втроём? | 19 | Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь – за 18 часов. За сколько часов мальчики покрасят забор, работая втроём? | ||
20 | Два гонщика участвуют в гонках. Им предстоит проехать 99 кругов по кольцевой трассе протяжённостью 4 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 22 минуты. | 20 | Два гонщика участвуют в гонках. Им предстоит проехать 99 кругов по кольцевой трассе протяжённостью 4 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 22 минуты. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 20 минут после старта. Ответ дайте в км/ч. | ||
Два сплава меди и олова. Соотношение меди и олова в первом сплаве 1:3, во втором сплаве 2:5, в каком соотношении нужно смешать два сплава, чтобы получить новый сплав, в котором соотношение олова и меди будет 8:3?
КВАНТОВАЯ КАТ-КОЭФФИЦИЕНТ, ПРОПОРЦИЯ И ВАРИАЦИЯ-ВОПРОС БАНК
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Дата обновления: 27 июня 2022 г.
Текст Решение
Ответ
Правильный ответ B
Ответ
Пошаговое решение, разработанное экспертами, чтобы помочь вам в разрешении сомнений и получении отличных оценок на экзаменах.
Похожие видео
जिनमे कॉपर व टिन क्रमश : 1:3 2:5 अनुपात मे है। तो किस अनुप000
22545846
दो मिश्र धातुओ मे टिन तथा 1: 2 और 2: 3 के अनुपात मे।।।।।।। है है है है है है है है है है है यदि मिश्रधातुओ को 3: 4 (वजन) के अनुपात मे मिलाया जाता है, तो नए मिश Вивра मे टिन तथ तथ लोहे क कात क्या होग होग होग होग मे तथ तथ क क अनुपात क्या होगा?
22545886
दो मिश्रधातुओं कॉप औ तीन से बनी है पहली मिश्रधातु में कॉप औ तीन क अनुप अनुप पहली है औ में में में में में में में में में में में में में में में ध ध ध ध औ औ औ औ ध ध औenतुओं में में में ghro कॉप में औждями 3 часа!
22546101
60 кг. टिन के मात्रा होगी !
22546116
A и B представляют собой два сплава меди и олова, приготовленные путем смешивания соответствующих металлов в соотношении 5:3 и 5:11 соответственно. Если сплавы А и В смешать, чтобы получить третий сплав С с равным соотношением меди и олова, каково будет соотношение сплавов А и В в новом сплаве С?
Если сплавы А и В смешать, чтобы получить третий сплав С с равным соотношением меди и олова, каково будет соотношение сплавов А и В в новом сплаве С?
446657571
Два сплава меди и олова. Соотношение меди и олова в первом сплаве 1:3, во втором сплаве 2:5, в каком соотношении нужно смешать два сплава, чтобы получить новый сплав, в котором соотношение олова и меди будет 8:3?
446657818
एक मिश्रधातु में जिंक, कॉपर और टिन का अनुपात क्रमशः 2: 3: 1 है।।।।।।। दूसरी मिश्रधातु में कॉपर , टिन और सीसे का अनुपाा 3 यदि समान भार वाली इन मिशшить नए मिश्रधातु में सीसे का प्रति किलो भार बताएँ।
643304268
A и B представляют собой два сплава меди и олова, приготовленные путем смешивания соответствующих металлов в соотношении 5 : 3 и 5 : 11 соответственно. Если сплавы А и В смешать из третьего сплава С с равным содержанием меди и олова, каково будет соотношение сплавов А и В в новом сплаве С?
643341047
В сплаве 80% меди, а остальное олово. В другом сплаве 85% меди и 12% олова. В каком соотношении нужно смешать два сплава, чтобы в новой смеси было 15 % олова?
В другом сплаве 85% меди и 12% олова. В каком соотношении нужно смешать два сплава, чтобы в новой смеси было 15 % олова?
643372131
60 кг сплава А смешивают со 100 кг сплава В. Если сплав А содержит свинец и олово в соотношении 3:2, а сплав В содержит олово и медь в соотношении 1:4, количество олово в новом сплаве есть.
646459220
Два сплава состоят из меди и олова. Соотношение меди и олова в первом сплаве 1:3, во втором 2:5. В каком соотношении следует смешать два сплава, чтобы получить новый сплав, в котором соотношение олова и меди равно 8:3?
646929023
60 кг сплава А смешивают со 100 кг сплава В. Если сплав А содержит свинец и олово в соотношении 3:2, а сплав В содержит олово и медь в соотношении 1:4, количество олово в новом сплаве есть.
646929060
Сплав содержит медь и олово в соотношении 3:2. Если в этот сплав добавить 250 г меди, то количество меди в нем станет вдвое больше количества в нем олова. Каково количество в гма олова в сплаве?
646929080
Существует два вида сплавов олова и меди. Первый сплав содержит олово и медь, так что 93,33% из них составляет олово. Во втором сплаве 86,66% олова. Какой вес первого сплава надо смешать с каким-то весом второго сплава, чтобы получилась масса 50 кг, содержащая 90% олова?
Первый сплав содержит олово и медь, так что 93,33% из них составляет олово. Во втором сплаве 86,66% олова. Какой вес первого сплава надо смешать с каким-то весом второго сплава, чтобы получилась масса 50 кг, содержащая 90% олова?
646929159
60 кг сплава А смешивают со 100 кг сплава В. Если сплав А содержит свинец и олово в соотношении 3 : 2, а сплав В содержит олово и медь в соотношении 1 : 4, то количество олова в новом сплаве
647366844
Соотношение меди и олова в сплаве 3 : 2 Если в этот сплав смешать 250 кг меди, то количество присутствующей в нем меди станет вдвое больше количества олова присутствует в этом сплаве.
647441993
Математическая задача: два сплава — вопрос № 71574, смеси и растворы
Два сплава Y и Z состоят из цинка, олова и меди. В сплаве Y соотношение цинка к олову составляет 2:5, а отношение меди к олову — 4:3. Найдите соотношение меди:цинка:олова в сплаве Y.
Правильный ответ:
r = 6:20:15Пошаговое объяснение:
Y: Zn:Sn = 2:5 = 2x:5x = (2⋅ 3):(5⋅ 3) = 6:15 Cu:Sn = 4:3 = 4y:3z = (4⋅ 5):(3⋅ 5) = 20:15 r = Cu:Zn:Sn Cu :Sn = 6:15 Zn:Sn = 20:15 Cu:Zn:Sn = 6:20:15 r=6:20:15
Нашли ошибку или неточность? Не стесняйтесь
написать нам . Спасибо!
Спасибо!
Советы по использованию связанных онлайн-калькуляторов
Воспользуйтесь нашим калькулятором коэффициентов.
У вас есть система уравнений и вы ищете калькулятор системы линейных уравнений?
Для решения этой задачи по математике вам необходимо знать следующие знания:
- алгебра
- система уравнений
- основные функции
- Соотношение
единицы физических величин:
- МАСС
Темы:
- Смеси и растворы
Учистка. ПРОБЛЕМА. 14-летние
- Латунь
Латунь представляет собой сплав меди и цинка в соотношении 3:2. Сколько граммов весит деталь, для изготовления которой требуется 270 г меди? - Замок-музей
В Замковом музее было найдено множество средневековых пушек, изготовленных из пушек (пушка — сплав олова и меди в соотношении 1:9). Советники согласились, что пушки им не нужны, а на городской башне бросят новый колокол. Колокола изготовлены из
Колокола изготовлены из - Скульптура 3215
Латунь – это сплав меди и цинка в соотношении 3 к 2. Сколько меди и цинка нужно скульптору для изготовления латунной скульптуры, которая должна весить 15 кг? - Бронзовая медаль
Для производства 1 кг бронзы необходимо 0,95 кг меди, 0,04 кг олова и 0,01 кг цинка. Бронзовая медаль весит 8,5 г. Сколько меди, олова и цинка в медали? - CuZn
Латунь представляет собой сплав меди и цинка. 10-сантиметровый латунный куб весит 8,6 кг. Плотность меди 8930 кг/м 3 , плотность цинка 7130 кг/м³. Подсчитайте, сколько килограммов меди и цинка содержится в кубе. - Бронза, олово и медь
Бронза представляет собой сплав олова и меди. Сплав 10% олова и 90% меди — это Gunmetal. Это колокольный металл, если он содержит 20% олова и 80% меди. Сколько тонн расплавленного колокольного металла и меди необходимо для производства 100 тонн бронзы? - Бронза 37391
Бронза представляет собой сплав олова и меди. Медь 85% остальное олово. Сколько бронзы получится из 51 кг меди? Хватит ли нам 8 кг жести?
Медь 85% остальное олово. Сколько бронзы получится из 51 кг меди? Хватит ли нам 8 кг жести? - Сплав
Первый сплав представляет собой смесь двух металлов в соотношении 1:2; второй представляет собой смесь тех же металлов в соотношении 2:3. При каком соотношении мы помещаем эти два сплава в печь, чтобы получить новый металлический сплав с соотношением 17:27? (Все три соотношения c - Монеты
Деньги — монеты чеканятся из самой твердой бронзы, которая содержит медь и олово в соотношении 41:9. Сколько меди и олова в 2 кг бронзовых денег? - Алмаз 4695
Рукоятка изготовлена из сплава. Сплав находится в соотношении 6 частей золота, 3 частей свинца и 8 частей алмаза. Ручка весит 24 кг. Сколько весят золото и свинец? - (соответственно) 67854
Сплав меди и свинца представляет собой смесь этих металлов в соотношении 5:2 (соответственно). Вычислите в кг, сколько весит кусок этого сплава, если в нем всего на 150 кг меньше свинца, чем в меди. - Марганец
Марганцевая бронза содержит следующие металлы на фунт: 0,89 фунта меди, 0,10 фунта олова и 0,01 фунта марганца. Сколько меди содержится в вале весом 235 фунтов?
Сколько меди содержится в вале весом 235 фунтов? - Число 4
Число состоит из двух цифр. Сумма цифр равна 11. Если поменять местами цифры, исходное число увеличится на 9. Найдите исходное число - Бронза
В бронзе 80% меди и 20% олова. Сколько меди нам понадобится для производства бронзы, если у нас есть 39кг жести? - Законодательство 58863
Для изготовления золотого декоративного изделия мы сплавляем 250 г 18-каратного и 200 г 14-каратного золота с оловом. Сколько олова нужно добавить, чтобы получить 14,6-каратное золото? Выразите чистоту полученного золота в смысле применимого законодательства. - Кольцо
Кольца из сплава золота и меди весят 14,5 г и имеют объем 1,03 см³. Сколько в нем золота и сколько меди? Плотность металла: Au 19,3 г/см³ и Cu 8,94 кг·дм-3 - Три примера на миллион
A. Рассчитайте 1,5 ‰ из 4,5 литров крови. Выразите результат в миллилитрах. B. Рассчитайте три ‰ от € 50 000. C. Поднос, который они принесли с завтраком в постель хозяина, сделан из сплава, содержащего 830 ‰ серебра.

 Найдите массу третьего сплава. Ответ дайте в килограммах
Найдите массу третьего сплава. Ответ дайте в килограммах Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси?
Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 72-процентный раствор кислоты. Сколько килограммов 45-процентного раствора использовали для получения смеси? Сколько процентов составит концентрация получившегося раствора?
Сколько процентов составит концентрация получившегося раствора? Сколько килограммов винограда потребуется для получения 8 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды?
Сколько килограммов винограда потребуется для получения 8 килограммов изюма, если виноград содержит 82% воды, а изюм содержит 19% воды? Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 66%. Если бы стипендия дочери уменьшилась вчетверо, общий доход семьи сократился бы на 6%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 66%. Если бы стипендия дочери уменьшилась вчетверо, общий доход семьи сократился бы на 6%. Сколько процентов от общего дохода семьи составляет зарплата жены?
 Пробыв в пункте В 2 часа 40 минут, байдарка отправилась назад и вернулась в пункт А в 23:0023:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость байдарки равна 6 км/ч.
Пробыв в пункте В 2 часа 40 минут, байдарка отправилась назад и вернулась в пункт А в 23:0023:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость байдарки равна 6 км/ч. Мотоциклист приехал в город В на 4 часа раньше, чем велосипедист приехал в город А, а встретились они через 1 час 30 минут после выезда. Сколько часов затратил на путь из города В в город А велосипедист?
Мотоциклист приехал в город В на 4 часа раньше, чем велосипедист приехал в город А, а встретились они через 1 час 30 минут после выезда. Сколько часов затратил на путь из города В в город А велосипедист? За сколько часов выполнят заказ оба мастера, работая вместе?
За сколько часов выполнят заказ оба мастера, работая вместе? За сколько минут пропалывает грядку одна Даша?
За сколько минут пропалывает грядку одна Даша?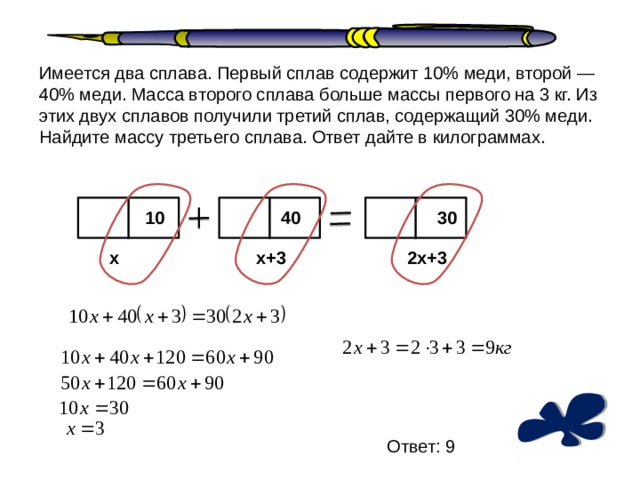 В первой бригаде было 9 рабочих, а во второй – 11 рабочих. Через 6 дней после начала работы в первую бригаду перешли 3 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Сколько дней потребовалось на выполнение заказов?
В первой бригаде было 9 рабочих, а во второй – 11 рабочих. Через 6 дней после начала работы в первую бригаду перешли 3 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Сколько дней потребовалось на выполнение заказов?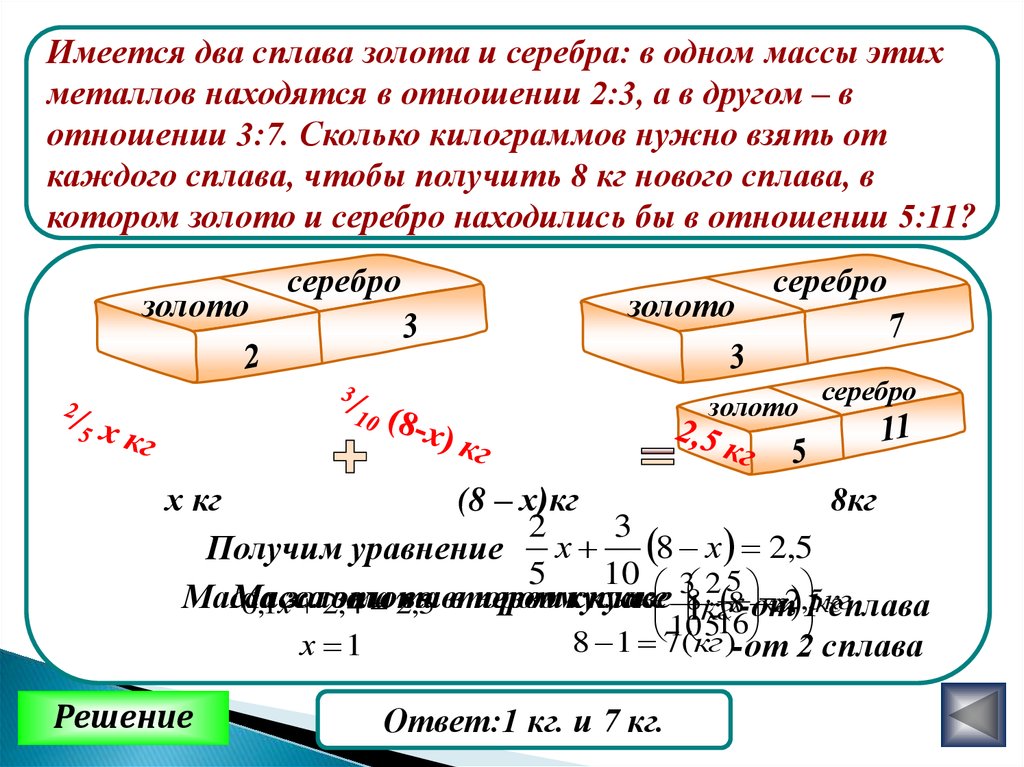 Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 20 минут после старта. Ответ дайте в км/ч.
Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 20 минут после старта. Ответ дайте в км/ч.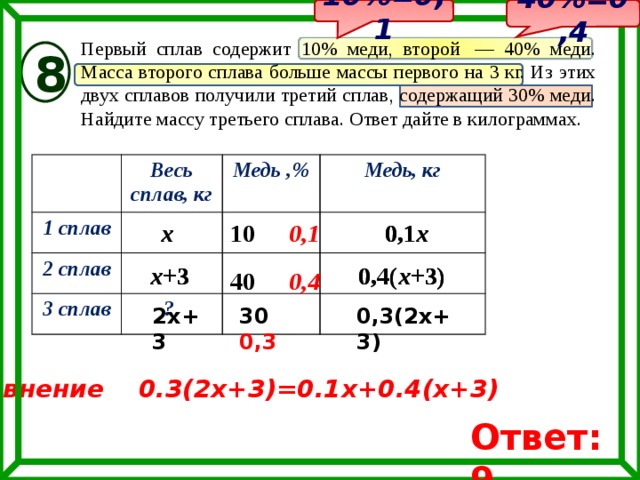 Колокола изготовлены из
Колокола изготовлены из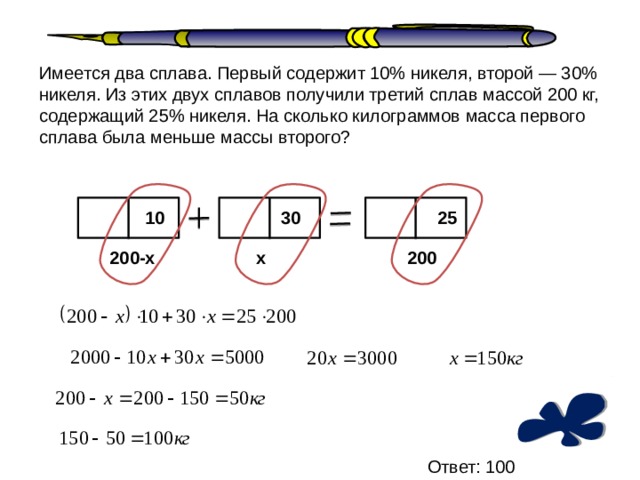 Медь 85% остальное олово. Сколько бронзы получится из 51 кг меди? Хватит ли нам 8 кг жести?
Медь 85% остальное олово. Сколько бронзы получится из 51 кг меди? Хватит ли нам 8 кг жести? Сколько меди содержится в вале весом 235 фунтов?
Сколько меди содержится в вале весом 235 фунтов?
Leave A Comment