Объем параллелепипеда abcda1b1c1d1 равен 3: Объем параллелепипеда равен

Объем параллелепипеда равен

Не откладывайте! ЗАГОВОРИТЕ на Английском!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

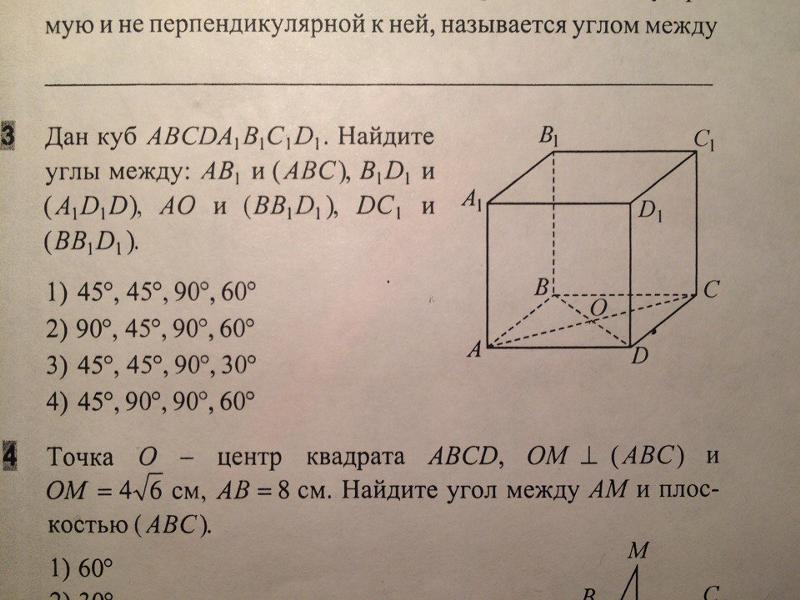
Александр | 2014-02-11

Для вас очередная статья, сегодня мы мы рассмотрим задания с параллелепипедом. Освежим в памяти само понятие…

Параллелепипед — это четырехугольная призма, все грани которой — параллелограммы. Параллелепипеды, как и призмы, могут быть прямыми и наклонными.

Если сказать просто, то у прямого параллелепипеда его боковые рёбра перпендикулярны основанию, боковые грани прямоугольники, основания параллелограммы; у наклонного параллелепипеда верхнее и нижнее основания как бы смещены параллельным сдвигом, посмотрите рисунок в первой задаче. 

В предыдущих статьях мы рассматривали задачи с прямоугольным параллелепипедом (все грани прямоугольники). Представленные ниже задания я выделил в отдельную группу, так как в ходе решения рассматривается пирамида — стоят вопросы о нахождении её объёма. Решаются они практически устно, но мы их разберём подробно. Что нужно помнить?

С площадью основания всё ясно. А что такое высота? Если параллелепипед прямой, то понятно – его высота равна боковому ребру. Если же  параллелепипед наклонный? Его высота равна расстоянию между основаниями, то есть простыми словами можно сказать, что это длина отрезка, который перпендикулярен основаниям и соединяет их:

Но в данных задачах находить саму площадь основания и высоту будет не нужно.

Формула объёма пирамиды:

*Запомните навсегда, что объём пирамиды равен одной трети объёма параллелепипеда с тем основанием и высотой.

Рассмотрим задачи:

Объем параллелепипеда равен 9. Найдите объем треугольной пирамиды ABDA₁.

Известно, что объём параллелепипеда равен произведению площади его основания и высоты, то есть:

Объём  пирамиды равен:

Рассмотрим пирамиду ABDA₁, её высота равна  высоте параллелепипеда, так она у них общая. Площадь её основания в два раза меньше площади основания параллелепипеда, так как диагональ BD делит параллелограмм ABCD на два равных по площади треугольника, значит:

Следовательно:

Получили, что объём пирамиды в шесть раз меньше объёма параллелепипеда и будет равен  9:6 = 1,5.

Ответ: 1,5

*В подобных заданиях, где дан объём параллелепипеда и требуется найти объём какой-либо составляющей его части, не нужно пытаться найти саму площадь основания или высоту. Необходимо просто установить соотношение объёмов используя известные свойства.

Объем куба равен 94. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

Объем призмы равен произведению площади основания на высоту:

Поскольку высота призмы равна высоте куба, то их объемы пропорциональны площадям их оснований. Определим, как соотносятся площади оснований призмы и куба.

Пусть ребро куба равно а. Тогда площадь основания куба равна а².

Определим площадь основания призмы:

Видно, что площадь основания построенной призмы в 8 раз меньше площади основания куба, поэтому искомый объем призмы также будет в 8 раз меньше объёма куба, то есть:

Ответ: 12

Объем куба равен 123. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Объем пирамиды равен:

Площади оснований куба и пирамиды равны, высота пирамиды в два раза меньше ребра куба. Обозначим ребро куба как  a, тогда объём пирамиды:

Ответ: 20,5

Объем параллелепипеда ABCDA₁B₁C₁D₁ равен 3,6. Найдите объем треугольной пирамиды B₁AD₁C.

Данную задачу можно решить разными способами. Можно найти площадь основания AD₁C и высоту пирамиды (отрезок соединяющий центр куба и вершину B₁), но это долгий путь. Проще поступить следующим образом.

Искомый объем равен разности объемов параллелепипеда и четырех пирамид:

То есть мы как бы вычленяем (вырезаем) пирамиду из куба «отсекая» лишнее. Обозначим для простоты восприятия рёбра следующим образом, пусть:

AB = a     BC = b     BB₁ = c

Тогда

Ответ: 1,2

Найдите объем параллелепипеда ABCDA₁B₁C₁D₁, если объем треугольной пирамиды ABDA₁ равен 10.

Эта задача обратная той, которую мы рассмотрели в самом начале. Мы установили, что объём такой пирамиды в шесть раз меньше объёма параллелепипеда, значит  объём параллелепипеда будет равен 60.

Запишем подробнее. Объем параллелепипеда равен:

Объём данной пирамиды равен:

Площадь основания пирамиды равна половине площади основания параллелепипеда, то есть:

Следовательно

Можем записать:

Ответ: 60

27182. Объем параллелепипеда ABCDA₁B₁C₁D₁ равен 12. Найдите объем треугольной пирамиды B₁ABC.  Ответ: 2

27183. Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

Посмотреть решение

27184. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Посмотреть решение

27209. Объем параллелепипеда ABCDA₁B₁C₁D₁ равен 4,5. Найдите объем треугольной пирамиды AD₁CB₁.

Посмотреть решение

77154. Найдите объем параллелепипеда ABCDA₁B₁C₁D₁, если объем треугольной пирамиды ABDA₁ равен 3.

Посмотреть решение

Как вы поняли, главное в подобных заданиях знать свойства. Например, что диагональ параллелограмма делит  его на два равных по площади треугольника; две диагонали параллелограмма разбивают его на четыре равных по площади треугольника; то, что центр куба делит его высоту пополам, равноотстоит от его граней и вершин и прочее.

Понимая это и другие простые свойства фигур вы без труда вычислите (устно) во сколько раз объём пирамиды будет меньше объёма куба или параллелепипеда, а также сможете быстро решать другие подобные задания.

Например, решим такую задачу: дан наклонный параллелепипед, его основание и основание пирамиды находятся в одной плоскости. Площадь основания пирамиды в 4 раза меньше, её высота в 3 раза меньше высоты параллелепипеда. Найдите объём пирамиды, если объём параллелепипеда равен 360.

Сразу отметим, что у пирамиды с тем же основанием и высотой объём в три раза меньше. Сказанной, что площадь её основания в 4 раза меньше, то есть объём уменьшается ещё в 4 раза, и высота в 3 раза, получаем:

Успеха вам!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Стереометрия ПРИЗМЫ | ЕГЭ-№2

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Объем пирамиды — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас.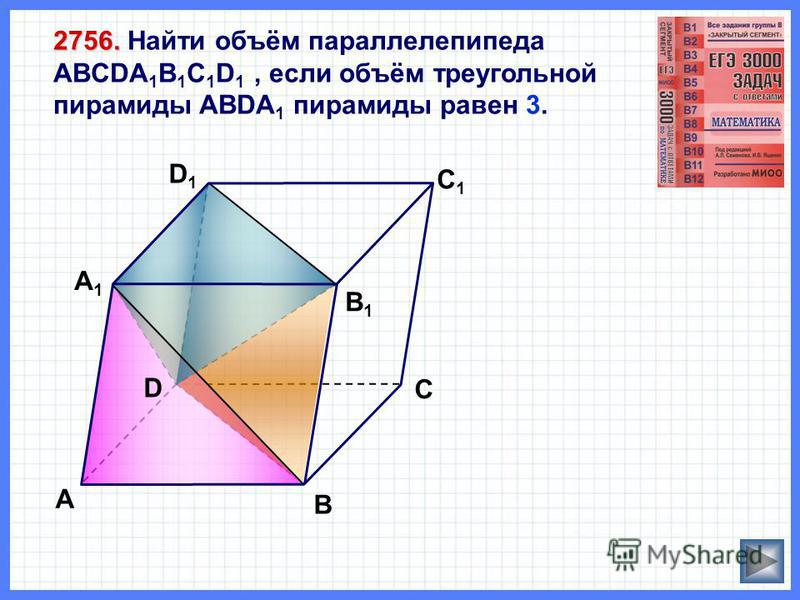 Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Открытый банк заданий по математике http://mathege.ru:8080/or/ege/Main.action
Во сколько раз увеличится объем правильного тетраэдра, если
все его ребра увеличить в два раза?
1
V = SoH
3
2h
h
a
1
S1 h2
V1
1
3
S = ab sin a
1

V2
2
S 2 h3
3
1 1 2
a sin 600 h
2
a
1
3 2
Найдем отношение
объемов
2
1 1
2
2a sin 600 2h 4a 2 8
3 2
2a
В9
8
3
10 х
х
Основанием пирамиды является прямоугольник со сторонами 3 и 4.
Ее объем равен 16. Найдите высоту этой пирамиды.
So 3 4 12
16
12
1
V = SoH
3
1
16 12 H
3
Н
4
3
16 4 H
H 4
В9
4
3
10 х
х
Найдите объем правильной треугольной пирамиды, стороны
основания которой равны 1, а высота равна 3.
11
1
V = SoH
3
3
1

600
1
S = ab sin a
2
1 1
V 1 1 sin 600 3
3 2
1
1
1 1 3
V
3
4
3 2 2
В9
0 , 25
3
10 х
х
Найдите высоту правильной
треугольной пирамиды, стороны
основания которой равны 2, а
объем равен 3.
600
1
S = ab sin a
2
1
1
3
0
S o 2 2 sin 60 2 2
3
2
2
2
V . 3
3
?
2
22
3
1
3 3 H : 3
3
1
1 H 3
3
1
V = SoH
3
2
H 3
В9
3
3
10 х
х
Во сколько раз увеличится объем пирамиды, если ее
высоту увеличить в четыре раза?
1
V = SoH
3
1
S о h2
h 1
V1
3
1
V2
Sо h3 4 h 4
3
Найдем отношение
объемов
F
h
4h
E
A
D
B
В9
4
C
3
10 х
х
Объем правильной шестиугольной пирамиды 6.
Сторона основания равна 1. Найдите боковое ребро.
S
11
600
V 6.
1
S = ab sin a
2
1
1
600
1
?
E
F
A
О
D
1
B
6
Vпир.
1
1
S0 6 1 1 sin 60 0
2
C
3 3
2
3 3 3
3 1 1
2
2
?
1
1 3 3
h; h
Sо h 6
3 2
3
Из АОS по теореме Пифагора
найди ребро AS.
В9
Можно
Для
правильного
вычислить6-уг.
сторона равна
площадь
правильного
радиусу
описанной
шестиугольника,
разбив
2 окружности.
12
его6на
6 треугольников.
;
h
3
7
3
3
10 х
х
.
В правильной четырехугольной пирамиде высота равна 6,
боковое ребро равно 10. Найдите ее объем.
1
V = SoH
3
.
Sкв.= a2
6
Н
10
1 2
V 10 6
3
10
В9
2 0 0
3
10 х
х
Основанием пирамиды служит прямоугольник, одна боковая грань
перпендикулярна плоскости основания, а три другие боковые грани
наклонены к плоскости основания под углом 600. Высота пирамиды
равна 6. Найдите объем пирамиды.
?6
1
V = SoH
3
S
Из SHG:
.
.
6
Из SHA:
D
600
A
Н
6
3
6
tg 60
;
HG
6
0
tg 60
;
AH
0
C
600
Sпр.= ab
G 12
3
B
1
V 24 6
3
S ABCD
В9
6
HG
3
6
AH
3
12
AD
3
12 6
24
3 3
4 8
3
10 х
х
Боковые ребра треугольной пирамиды взаимно перпендикулярны,
каждое из них равно 3. Найдите объем пирамиды.
A
S
высота
3
3
3
3
C
С
3
S
A
3
В
1
V = SoH
3
1
S = ab
2
1 1
V 3 3 3
3 2
B
33
Задача очень простая, если догадаться
опрокинуть пирамиду на удобную грань,
например, SCB.
Основание – прямоугольный треугольник
SCB, высота AS.
В9
4 , 5
3
10 х
х
Сторона основания правильной шестиугольной пирамиды равна 4,
а угол между боковой гранью и основанием равен 450.
Найдите объем пирамиды.
44
600
?
?
1
К4
1
S
4
S = ab sin a
V = SoH
2
.
3
0
О
2
60
4
С
.
2 3
E
F
О
A
4
B
4
1
S0 6 4 4 sin 600 Найдем ОК по
2
теореме Пифагора
450
C

D
К
1
V 24 3 2 3
3
3
3 4 4
24 3
2
ОК
Можно вычислить
2
2площадь правильного
4 2 шестиугольника,
12 2 3разбив
;
его на 6 треугольников.
SOK р / б , ОК OS 2 3
В9
4 8
3
10 х
х
Объем параллелепипеда ABCDA1B1C1D1 равен 12.
Найдите объем треугольной пирамиды B1ABC.
2SABC
Vприз. = SoH
Vприз.
Vпир.
1
Vпир. = SoH
3
D1
C1
h
A1
B1
D
A
h
S ABCD h
2 S ABC
6
1
1
S ABC h
S ABC 1
3
3
Найдем отношение объемов
V12приз.
C
Vпир.
6
1
B
В9
2
3
10 х
х
Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объем
треугольной пирамиды AD1CB1.
2SABC
Пирамида AD1CB1 получается, если мы отрежем от параллелепипеда
V
SoH по углам
h 1, AA12DS1BABC
Vпар.
четыре
— ABCBS
D1B1CC
пар. =пирамиды
1, ABCD
1 и ADCD1. А объем
мы1делали это в1предыдущей задаче.
каждой из них легко посчитать —
Например, найдем объемVпирамиды
ABCB
пир.
S 1.h
S
1
Vпир. = SoH
3
3
V
3
6
;
1
ABC
4,5
C1 Найдем
пар . отношение объемов
D1
A1
Vпир.
B1
Vпир.
3
4
Четыре пирамиды по углам — ABCB1, D1B1CC1,
AA1D1B1 и ADCD1
3
h
D
C
A
ABC
6
1
4Vпир. 4
Объем пирамиды АD1CB1
4
3
VAD1CB1 4,5 3 1,5
B
В9
1 , 5
3
10 х
х
Объем куба равен 12. Найдите объем четырехугольной пирамиды,
основанием которой является грань куба, а вершиной — центр куба.
Найдем отношение объемов
Vкуб. S o h
Vкуб.
1
Vпир. = SoH
3
D1
C1
A1
B1
D
A
Vпир.
S ABCD h
1
6
1
1
1
1
S ABCD h
3
2
6
1
2
h
h
Vкуб .
12
Vпир.
6
1
C
B
В9
2
3
10 х
х
От треугольной призмы, объем которой равен 150, отсечена
треугольная пирамида плоскостью, проходящей через сторону одного
основания и противоположную вершину другого основания.
Найдите объем оставшейся части.
Vприз. = SoH
Vпир. =
Vприз.
1
SoH
3
Vпир.
3
Sо h
1
1
Sо h
3
Найдем отношение объемов
h
V150
приз.
Vпир.
В9
3
1
5 0
3
10 х
х
Объем треугольной пирамиды SABC, являющейся частью
правильной шестиугольной пирамиды SABCDEF, равен 8. Найдите
объем шестиугольной пирамиды.
У треугольной и шестиугольной пирамид,1о которых говорится в условии,
1
Vпир.
S 6 hрасположение букв…
одинаковые
в этом,
изменим
1
Vпир. = высоты.
SoH Убедимся
3 различна.
Одинаковая3высота, но площадь оснований
Vпир. 2
1
S АВС h
3
S
6
1
Найдем отношение объемов
V1
Vпир.1
D
E
Vпир.2
8
C
D
F
E
B
C
A
F
A
B
V2
6
1
Поработаем с выносным чертежом.
Видим, что площадь основания
треугольной пирамиды в 6 раз
меньше, чем у шестиугольной.
В9
4 8
3
10 х
х
Объем правильной четырехугольной пирамиды SABCD равен 12.
Точка E — середина ребра SB. Найдите объем треугольной
пирамиды EABC.
Точка E – середина ребра SB, значит, точка N – середина SO (по т. Фалеса).
Высота пирамиды EABC равна половине высоты пирамиды SABCD.

2SABC
1
Vпир. = SoH
3
Vпир.1
S
Vпир. 2
N
D
A
1
2
1
S ABCD h
2 S ABC
4
3
1 1
1
1
S АВС h S АВС 2
3
2
Найдем отношение объемов
E
V12
пир.1
h
C
Vпир. 2
4
1
O
B
В9
3
3
10 х
х
От треугольной пирамиды, объем которой равен 12, отсечена
треугольная пирамида плоскостью, проходящей через
1
вершину пирамиды и среднюю линию основания.
S = ab sin a
Найдите объем отсеченной треугольной пирамиды.
2
У треугольной пирамиды и отсеченной пирамиды, о которых говорится
1одинаковые высоты. Убедимся в этом, изменим расположение букв…
в
1
Vусловии,
=
SoH
1
пир.
Одинаковая
различна.ab sin C
3 высота, но площадь оснований
S
h
NCM
Vпир.1Работать
3 можно с любым2 из этих чертежей.
S
Vпир. 2
1
S
1
1
4
S ABC h
2a 2b sin C
3
2
Найдем отношение объемов
Vпир.1
V2
B
A
М
a
V1
C
b
N
V12
пир.2
1
4
М
С
В
В9
3
А
N
3
10 х
х
Объем треугольной пирамиды равен 15. Плоскость проходит
через сторону основания этой пирамиды и пересекает противоположное
боковое ребро в точке, делящей его в отношении 1 : 2, считая от
вершины пирамиды. Найдите больший из объемов пирамид, на которые
плоскость разбивает исходную пирамиду.
Надо сравнить объемы пирамид NABC и NSAC. Найдем объем пирамиды NABC.
1
Затем из VSABC (это 15) вычтем VNABC,, найдем
S ABCVNSAC
h .
VSABC объем3пирамиды NABC. Сравним его с
Найдем
S
составив отношение.
объемом
всей пирамиды SABC,
2
VОснования
у1
них одинаковые
– треугольник АВС.
NABC
S
h
А высоты разные,АВС
сравним их.
3
2
3
2
3
A
По т. Фалеса FP:SP = 2:3.
2
2
15
Тогда,
если SP=h, то FP= h, NO= h
SABC
3
3
N
F
3
V
3
VNABC 2
VNABC 10;
h
B
O
P
VNSAC 15 10 5.
В9
C
1 0
3
10 х
х

English     Русский Правила

Калькулятор объема параллелепипеда

Создано Кришной Нелатуру

Отредактировано Стивеном Вудингом

Последнее обновление: 02 февраля 2023 г.

Содержание:

• Формула объема параллелепипеда ?
• Как вычислить объем параллелепипеда по сторонам?
• Как рассчитать площадь поверхности параллелепипеда?
• Как использовать этот объем калькулятора параллелепипеда – И калькулятор площади параллелепипеда
• FAQ

Этот калькулятор объема параллелепипеда поможет вам вычислить объем параллелепипеда из его трех векторов , четырех вершин или длин ребер . Кроме того, он также рассчитает площадь параллелепипеда. Вам интересно, как найти объем параллелепипеда , образованного тремя векторами ? Хочешь узнать формулу объема параллелепипеда с четыре вершины ? Читайте дальше, чтобы узнать ответы на все эти и другие вопросы.

Объем параллелепипеда формула

Параллелепипед – это многогранник , у которого шесть граней являются параллелограммами . Для описания параллелепипеда нам нужны его три смежные стороны и их углы или три смежных вектора .

Три взаимно-начальных вектора в пространстве описывают параллелепипед.

Формула для объема параллелепипеда определяется как:

V=∣(a⃗×b⃗)⋅c⃗ ∣V = \lvert (\vec{a}\times\vec{b})\cdot\vec{c } \, \ rvertv = ∣ (A

× B

) ⋅C

∣

Где:

• VVV — Том из параллелепиппа сформированы на Three Vectors ; и
• a⃗\vec{a}a, b⃗\vec{b}b и c⃗\vec{c}c – Три вектора , которые описывают три смежных (и уникальных) сторон параллелепипеда .

Умножение векторов выше называется скалярным тройным произведением (или тройным произведением). Он включает перекрестное произведение векторов a⃗\vec{a}a и b⃗\vec{b}b, в результате чего получается вектор a⃗×b⃗\vec{a}\times\vec{b}a×b перпендикуляр к a⃗\vec{a}a и b⃗\vec{b}b. Воспользуйтесь нашим калькулятором перекрестных произведений, если хотите узнать больше о перекрестных произведениях.

🔎 Обратите внимание, что векторная величина равнодействующей, ∣a⃗×b⃗∣\lvert\vec{a} \times \vec{b}\rvert∣a×b∣, равна площадь параллелограмма , описываемая этими двумя векторами.

Последующее скалярное произведение между a⃗×b⃗\vec{a}\times\vec{b}a×b и c⃗\vec{c}c обозначает проекцию a⃗×b⃗\vec{a}\ раз\vec{b}a×b на c⃗\vec{c}c. Другими словами, он перемещает основание параллелограмма вдоль c⃗\vec{c}c, аналогично умножению площади основания на высоту .

Формулу можно упростить и свести к одному определителю:

V=∣(a⃗×b⃗)⋅c⃗∣=∣∣ijka1a2a3b1b2b3∣⋅(c1i+c2j+c3k)∣⟹V=∣c1c2c3a1b2scripta3\ \начать{выравнивать*} V &= \lvert (\vec{a}\times\vec{b})\cdot\vec{c}\, \rvert\\\\ &= \lvert\begin{vmatrix} \bm{i} и \bm{j} и \bm{k}\\ а_1 и а_2 и а_3\\ б_1 и б_2 и б_3 \end{vmatrix}\cdot (c_1\bm{i} + c_2\bm{j} + c_3\bm{k}) \rvert\\\\ \подразумевает V & = \begin{vmatrix} c_1 и c_2 и c_3\\ а_1 и а_2 и а_3\\ б_1 и б_2 и б_3 \end{vmatrix} \end{align*}V⟹V​=∣(a

×b

)⋅c

∣=∣∣

∣​ia1​b1​​ja2​b2​​ka3​b3​∣

∣​⋅(c1​i+c2​j ​k)∣=∣

∣​c1​a1​b1​​c2​a2​b2​​c3​a3​b3​∣

∣​​

Где:

• a1a_1a1​, a2a_2a2​,​​, a2a_2a2 a3a_3a3​ – Компоненты из a⃗\vec{\bm{a}}a;
• b1b_1b1​, b2b_2b2​, b3b_3b3​ – Компоненты из b⃗\vec{\bm{b}}b;
• c1c_1c1​, c2c_2c2​, c3c_3c3​ – Компоненты из c⃗\vec{\bm{c}}c; и
• i\bm{i}i, j\bm{j}j, k\bm{k}k – Единичные векторы вдоль координатных осей .

Наш калькулятор определителя матрицы может помочь вам понять и вычислить определители.

Теперь, когда вы знаете, как найти объем параллелепипеда с векторами, давайте узнаем, что делать, если единственными заданными значениями являются вершины параллелепипеда .

Зная вершины смежных сторон, мы можем определить векторы.

Вы можете найти любой вектор между двумя точками по координатам этих точек с помощью нашего векторного калькулятора. Как только вы определите векторы, вы можете рассчитать объем параллелепипеда, используя приведенную выше формулу.

Как рассчитать объем параллелепипеда?

Чтобы вычислить объем параллелепипеда , образованного векторами a , b и c 9 , выполните следующие простые шаги 9 :0003

1. Найдите векторное произведение между векторами a и b , чтобы получить a × b 90.
2. Вычислите скалярное произведение между векторами a × b и c , чтобы получить скалярное значение (a × b) ∙ 90,49 c 90,49 90,9 0,49 9 0,4 9 0,4 9 0,4 9 0 9 0, 4 9
3. Определить объем параллелепипеда как абсолютное значение этого скаляра, заданное как ∣(a × b) ∙ c∣ .

Например, рассмотрим параллелепипед, образованный векторами a⃗=i+2j+3k\vec{\bm{a}} = \bm{i} + 2\bm{j} + 3\bm{k}a =i+2j+3k, b⃗=5i−4j+7k\vec{\bm{b}} = 5\bm{i} - 4\bm{j} + 7\bm{k}b=5i-4j+ 7k и c⃗=−5i+j+12k\vec{\bm{c}} = -5\bm{i} + \bm{j} + 12\bm{k}c=-5i+j+12k. Тогда объем параллелепипеда, описываемого этими векторами, будет равен

V=∣(a⃗×b⃗)⋅c⃗ ∣=∣−51121235−47∣V=290\начать{выровнять*} V &= \lvert (\vec{a}\times\vec{b})\cdot\vec{c}\, \rvert\\\\ &= \begin{vmatrix} -5 и 1 и 12\\ 1 и 2 и 3\\ 5 и -4 и 7 \end{vmatrix}\\\\ V & = 290 \end{align*}VV​=∣(a

×b

)⋅c

∣=∣

∣​−515​12−4​1237​∣

∣​=2904 0004​ 00043​ вычислить объем параллелепипеда из его сторон?

Чтобы вычислить объем параллелепипеда из его сторон (или длин ребер ), используйте формулу ) - cos 2 (β) - cos 2 (γ)) , где:

• V – Объем параллелепипеда;
• a , b и c – Три смежные стороны параллелепипеда;
• α – Уголок между бортами б и с ;
• β – Угол между сторонами a и c ; и
• γ – Угол между сторонами a и b .

Параллелепипед с длинами ребер и углами.

Например, рассмотрим параллелепипед ABCDEFGH с длинами ребер a=5a = 5a=5, b=4b = 4b=4 и c=7c = 7c=7. Если ∠DAE=45°\угол \text{DAE} = 45\градус∠DAE=45°, ∠BAD=63°\угол \text{BAD} = 63\градус∠BAD=63° и ∠BAE=50 °\угол \text{ВАЕ} = 50\градус∠ВАЕ=50°, тогда объем параллелепипеда будет В = 5·4·7 √(1 + 2·cos(45)·cos(50)·cos(63) - cos 2 (45°) - cos 2 (50°) - cos 2 (63 °) = 75,83 .

Как я рассчитал площадь поверхности параллелепипена?

, и c , используйте формулу A = 2 × (∣a × b∣ + ∣b × c∣ + ∣a × c∣) , где:

• ∣a × b∣ – Величина перекрестного произведения между a и b 90;
• ∣b × c∣ – Величина перекрестного произведения между b и c ; и
• ∣a × c∣ – Величина перекрестного произведения между а и с .

Кроме того, вы можете найти площадь поверхности из длин ребер a , b и c , используя формулу A = 2 × (a∙b∙sin(γ) + b∙c ∙sin(α) + a∙c∙sin(β)) , где:

• α – Угол между b и c ;
• β – Угол между a и c ; и
• γ – Угол между a и b .

Обратите внимание, что величина перекрестного произведения между двумя векторами a⃗\vec{a}a и b⃗\vec{b}b, заданная как ∣a⃗×b⃗∣\lvert \vec{a} \ раз \vec{b} \rvert∣a×b∣ равно площади параллелограмма , натянутого на эти векторы. Следовательно, сложив величины перекрестных произведений трех векторов , описывающий параллелепипед , и умножив его на два, получим его площадь поверхности .

Например, рассмотрим параллелепипед ABCDEFGH с длинами ребер a=5a = 5a=5, b=4b = 4b=4 и c=7c = 7c=7. Если ∠DAE=45°\угол \text{DAE} = 45\градус∠DAE=45°, ∠BAD=63°\угол \text{BAD} = 63\градус∠BAD=63° и ∠BAE=50 °\угол \text{BAE} = 50\градус∠BAE=50°, тогда площадь поверхности будет равна

A= 2×(absin⁡(α)+bcsin⁡(β)+acsin⁡(γ) )= 2×(5⋅4sin⁡(63°)+4⋅7sin⁡(45°)+5⋅7sin⁡(50°))= 132,6\scriptsize \begin{align*} A =&\ 2 \times (ab\sin(α) + bc\sin(β) + ac\sin(γ))\\ =&\ 2 \times (5\cdot 4 \sin(63\степень) + 4\cdot7\sin(45\степень) \\ &+ 5\cdot 7 \sin(50 \степень))\\ =&\ 132,6 \end{align*}A===​ 2×(absin(α)+bcsin(β)+acsin(γ)) 2×(5⋅4sin(63°)+4⋅7sin(45°)+5⋅ 7sin(50°)) 132,6​

Как использовать этот объем калькулятора параллелепипеда – И калькулятор площади параллелепипеда

Этот объем калькулятора параллелепипеда является простым инструментом и легким в использовании. Он имеет три различных режима расчета, чтобы найти объем параллелепипеда с 3 векторами, 4 вершинами или с использованием длин ребер и углов:

1. Чтобы вычислить объем параллелепипеда по 3 векторам:

   • Выберите опцию векторы aaa, bbb и ccc в поле Расчет с использованием поля .
   • Введите значения компонентов каждого вектора.
   • Калькулятор этого объема параллелепипеда отобразит расчетный объем и площадь поверхности параллелепипеда в соответствующих полях раздела Результаты .

2. Чтобы вычислить объем параллелепипеда с 4 вершинами:

   • Выберите опцию vertices p, q, r и s в поле Расчет с использованием поля .
   • Введите координаты каждой вершины в соответствующее поле.
   • Калькулятор отобразит вычисленные объем и площадь поверхности параллелепипеда в соответствующих полях раздела Результаты .

3. Чтобы вычислить объем параллелепипеда, используя длины ребер:

   • Выберите опцию Длины и углы ребер в поле Расчет с использованием поля .
   • Введите длины и углы ребер в соответствующие поля.
   • Калькулятор отобразит вычисленные объем и площадь поверхности параллелепипеда в соответствующих полях раздела Результаты .

⚠️ Если ваш ввод равен , который не принимается в каком-либо режиме расчета, это происходит потому, что вы ввели значения в другом режиме расчета, что делает невозможным обработку значений в текущем. Чтобы решить эту проблему, нажмите Перезагрузите кнопку в левом нижнем углу и снова введите значения, выбрав нужный режим расчета.

Часто задаваемые вопросы

Как определить, являются ли три вектора компланарными или коллинеарными?

• If the volume of a parallelepiped described by the vectors a , b , and c is equal to zero , then the vectors are coplanar . Другими словами, векторы a , b и c лежат в одной плоскости, если

• If the surface area of a parallelepiped formed by the vectors a , b , and c is equal to zero , then the vectors are collinear . Другими словами, векторы a , b и c коллинеарны, если 2 × (∣a × b∣ + ∣b × c∣ = 0 .

Сколько параллельных граней в параллелепипеде?

В параллелепипеде три пары параллельных граней. Попробуйте быстро произнести это предложение: Три пары параллельных параллелограммов в параллелепипеде!

Кришна Нелатуру

Рассчитайте с использованием . ..

Компоненты вектора 𝗮 (A₁𝗶 + A₂𝗷 + A₃𝗸)

Компоненты вектора 𝗯 (B₁𝗶 + B₂𝗷 + B₃𝗸)

Компоненты вектора 𝗰 (C₁𝗶 + C₃𝗸)

Результаты

Объем параллелепипеда

Площадь поверхности параллелепипеда

Посмотреть 41 аналогичный калькулятор координатной геометрии 📈

Средняя скорость изменения Билинейная интерполяцияКатенарная кривая… еще 38

Как найти объем параллелепипеда из его смежных ребер — Криста Кинг Математика

Формулы объема параллелепипеда

Если нам нужно найти объем параллелепипеда и нам даны три его смежных ребра, все, что нам нужно сделать, это найти скалярное тройное произведение трех векторов, определяющих ребра:

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

???|\vec{PS}\cdot(\vec{PQ}\times \vec{PR})|???

где ???\vec{PS}???, ???\vec{PQ}??? и ???\vec{PR}??? являются тремя соседними ребрами.

Сначала найдем векторы ???\vec{PQ}???, ???\vec{PR}??? и ???\vec{PS}???, то мы найдем векторное произведение ???\vec{PQ}\times \vec{PR}??? используя ???3\times 3??? матрица

???\begin{vmatrix}\bold i&\bold j&\bold k\\PQ_1&PQ_2&PQ_3\\PR_1&PR_2&PR_3\end{vmatrix}=\bold i\begin{vmatrix}PQ_2&PQ_3\\PR_2&PR_3\end{vmatrix}- \bold j\begin{vmatrix}PQ_1&PQ_3\\PR_1&PR_3\end{vmatrix}+\bold k\begin{vmatrix}PQ_1&PQ_2\\PR_1&PR_2\end{vmatrix}???

???=(PQ_2PR_3-PQ_3PR_2)\жирный i-(PQ_1PR_3-PQ_3PR_1)\жирный j+(PQ_1PR_2-PQ_2PR_1)\жирный k???

Мы преобразуем результат перекрестного произведения в стандартную векторную форму, а затем возьмем скалярное произведение ???\vec{PS}\langle{PS_1},PS_2,PS_3\rangle??? и векторный результат ???\vec{PQ}\times\vec{PR}???. Окончательный ответ — это значение скалярного тройного произведения, равного объему параллелепипеда.

Как найти объем параллелепипеда по трем векторам, определяющим его ребра

Пройти курс

Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого.

🙂

Построение трех векторов по четырем точкам, затем по векторам нахождение объема параллелепипеда

Пример

Нахождение объема параллелепипеда, заданного смежными ребрами ???\vec{PQ}??? , ???\vec{PR}??? и ???\vec{PS}???.

???Р(5,1,-2)???

???Q(0,-1,3)???

???R(3,2,-4)???

???S(1,-2,0)???

Нам нужно начать с использования четырех точек, чтобы найти векторы ???\vec{PQ}???, ???\vec{PR}??? и ???\vec{PS}???, так как это три смежных ребра параллелепипеда.

???\vec{PQ}=\langle0-5,-1-1,3-(-2)\rangle???

???\vec{PQ}=\langle-5,-2,5\rangle???

и

???\vec{PR}=\langle3-5,2-1,-4-(-2)\rangle???

???\vec{PR}=\langle-2,1,-2\rangle???

и

???\vec{PS}=\langle1-5,-2-1,0-(-2)\rangle???

???\vec{PS}=\langle-4,-3,2\rangle???

Окончательный ответ — это значение скалярного тройного произведения, равного объему параллелепипеда.

Теперь нам нужно взять векторное произведение ???\vec{PQ}??? и ???\vec{PR}???.

???\vec{PQ}\times\vec{PR}=\begin{vmatrix}\bold i&\bold j&\bold k\\-5&-2&5\\-2&1&-2\end{vmatrix}? ??

???\vec{PQ}\times\vec{PR}=\bold i\begin{vmatrix}-2&5\\1&-2\end{vmatrix}-\bold j\begin{vmatrix}-5&5\ \-2&-2\end{vmatrix}+\жирный k\begin{vmatrix}-5&-2\\-2&1\end{vmatrix}???

???\vec{PQ}\times\vec{PR}=\left[(-2)(-2)-(5)(1)\right]\bold i-\left[(-5) (-2)-(5)(-2)\вправо]\жирный j+\влево[(-5)(1)-(-2)(-2)\вправо]\жирный k???

???\vec{PQ}\times\vec{PR}=(4-5)\жирный i-(10+10)\жирный j+(-5-4)\жирный k???

???\vec{PQ}\times\vec{PR}=-\жирный i-20\жирный j-9\жирный k???

???\vec{PQ}\times\vec{PR}=\langle-1,-20,-9\rangle???

Скалярное произведение ???\vec{PS}=\langle-4,-3,2\rangle??? и ???\vec{PQ}\times\vec{PR}=\langle-1,-20,-9\rangle???, получаем

???\left|\vec{PS}\cdot \left(\vec{PQ}\times\vec{PR}\right)\right|=(-4)(-1)+(-3)(-20)+(2)(-9)???

???\влево|\vec{PS}\cdot\влево(\vec{PQ}\times\vec{PR}\вправо)\вправо|=4+60-18???

???\left|\vec{PS}\cdot\left(\vec{PQ}\times\vec{PR}\right)\right|=46???

Объем параллелепипеда ???46???.