Импульс — Физика — Теория, тесты, формулы и задачи
Оглавление:
- Основные теоретические сведения
- Импульс тела
- Закон сохранения импульса
- Сохранение проекции импульса
- Многомерный случай ЗСИ. Векторный метод
Импульс тела
К оглавлению…
Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:
Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с.
Общий импульс системы тел равен векторной сумме импульсов всех тел системы:
Изменение импульса одного тела находится по формуле (обратите внимание, что разность конечного и начального импульсов векторная):
где: pн – импульс тела в начальный момент времени, pк – в конечный. Главное не путать два последних понятия.
Главное не путать два последних понятия.
Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т.п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения.
Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.
Закон сохранения импульса
К оглавлению…
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.
Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса (ЗСИ). Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:
Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось. Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.
Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.
Сохранение проекции импульса
К оглавлению…
Возможны ситуации, когда закон сохранения импульса выполняется только частично, то есть только при проектировании на одну ось. Если на тело действует сила, то его импульс не сохраняется. Но всегда можно выбрать ось так, чтобы проекция силы на эту ось равнялась нулю. Тогда проекция импульса на эту ось будет сохраняться. Как правило, эта ось выбирается вдоль поверхности по которой движется тело.
Многомерный случай ЗСИ. Векторный метод
К оглавлению…
В случаях если тела движутся не вдоль одной прямой, то в общем случае, для того чтобы применить закон сохранения импульса, нужно расписать его по всем координатным осям, участвующим в задаче. Но решение подобной задачи можно сильно упростить, если использовать векторный метод. Он применяется если одно из тел покоится до или после удара. Тогда закон сохранения импульса записывается одним из следующих способов:
Но решение подобной задачи можно сильно упростить, если использовать векторный метод. Он применяется если одно из тел покоится до или после удара. Тогда закон сохранения импульса записывается одним из следующих способов:
В этих формулах буквой υ обозначены скорости тел до соударения, а буквой u обозначены скорости тел после соударения. Из правил сложения векторов следует, что три вектора в этих формулах должны образовывать треугольник. Для треугольников применяется теорема косинусов. Если правильно записать соответствующую теорему косинусов, то зачастую получается уравнение из которого можно найти нужную величину. Однако, иногда к правильно записанной теореме косинусов еще нужно будет добавить правильно записанный закон сохранения энергии (смотрите следующий раздел). В этом случае получится система уравнений из которых наверняка можно будет найти нужную величину.
Закон сохранения импульса — опредление, формулы, формулировка
Покажем, как применять знание физики в жизни
Начать учиться
189. 2K
2K
Физика — такая клевая наука, в которой ничего не исчезает бесследно. Вот и импульс не отстает. О том, что такое импульс, каким образом он сохраняется и при чем тут медузы — читайте в этой статье.
Импульс: что это такое
Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.
Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.
Импульс тела p — импульс тела [кг · м/с] v — скорость [м/с] |
Пятерка по физике у тебя в кармане!
Решай домашку по физике на изи. Подробные решения помогут разобраться в сложной теме и получить пятерку!
Подробные решения помогут разобраться в сложной теме и получить пятерку!
Закон сохранения импульса
В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:
Закон сохранения импульса
|
А выглядит — вот так:
Закон сохранения импульса
|
Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Решение:
Запишем закон сохранения импульса для данного процесса.
— это импульс системы мальчик + лодка до того, как мальчик спрыгнул,
— это импульс мальчика после прыжка,
— это импульс лодки после прыжка.
Изобразим на рисунке, что происходило до и после прыжка.
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
Подставим формулу импульса.
, где:
— масса мальчика [кг]
— скорость мальчика после прыжка [м/с]
— масса лодки [кг]
— скорость лодки после прыжка [м/с]
Выразим скорость лодки :
Подставим значения:
м/с
Ответ: скорость лодки после прыжка равна 0,5 м/с
Задачка посложнее
Тело массы m1 = 800 г движется со скоростью v1 = 3 м/с по гладкой горизонтальной поверхности. Навстречу ему движется тело массы m2 = 200 г со скоростью v2 = 13 м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.
Навстречу ему движется тело массы m2 = 200 г со скоростью v2 = 13 м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.
Решение: Для данной системы выполняется закон сохранения импульса:
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.
Спроецируем импульсы на ось х:
После неупругого удара получилось одно тело массы , которое движется с искомой скоростью:
Отсюда находим скорость тела, образовавшегося после удара:
Переводим массу в килограммы и подставляем значения:
м/с
В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.
Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X.
Ответ: скорость системы тел после соударения равна v = 0,2 м/с.
Второй закон Ньютона в импульсной форме
Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:
Применим выражение для ускорения
В этих уравнениях слева находится величина a. Так как левые части уравнений равны, можно приравнять правые их части
Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:
В правой части находится — это разница между конечной и начальной скоростью.
Преобразуем правую часть
Раскрыв скобки, получим
Заменим произведение массы и скорости на импульс:
Подставляем:
Или, сокращенно:
То есть, вектор – это вектор изменения импульса .
Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.
Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как? |
Решение:
Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).
Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.
Реактивное движение
В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется
Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.
Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:
Сила называется реактивной. Это та сила, которая возникает в процессе отделения части тела.
Закон сохранения импульса позволяет оценить скорость ракеты.
mг · vг = mр · vр,
где mг — это масса горючего,
vг — скорость горючего,
mр — масса ракеты,
vр — скорость ракеты.
Отсюда можно выразить скорость ракеты:
vр = mг · vг / mр
vр = mг · vг / mр vг — скорость горючего [м/с] mр — масса ракеты [кг] vр — скорость ракеты [м/с] |
Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.
Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Карина Хачатурян
К предыдущей статье
Взаимодействие тел
К следующей статье
197.8K
Сила упругости
Получите индивидуальный план обучения физике на бесплатном вводном уроке
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Импульс — измерение, объект, частицы и положение
Импульс — это свойство движения , которое в классической физике является векторной (направленной) величиной, которая в замкнутых системах сохраняется при столкновениях.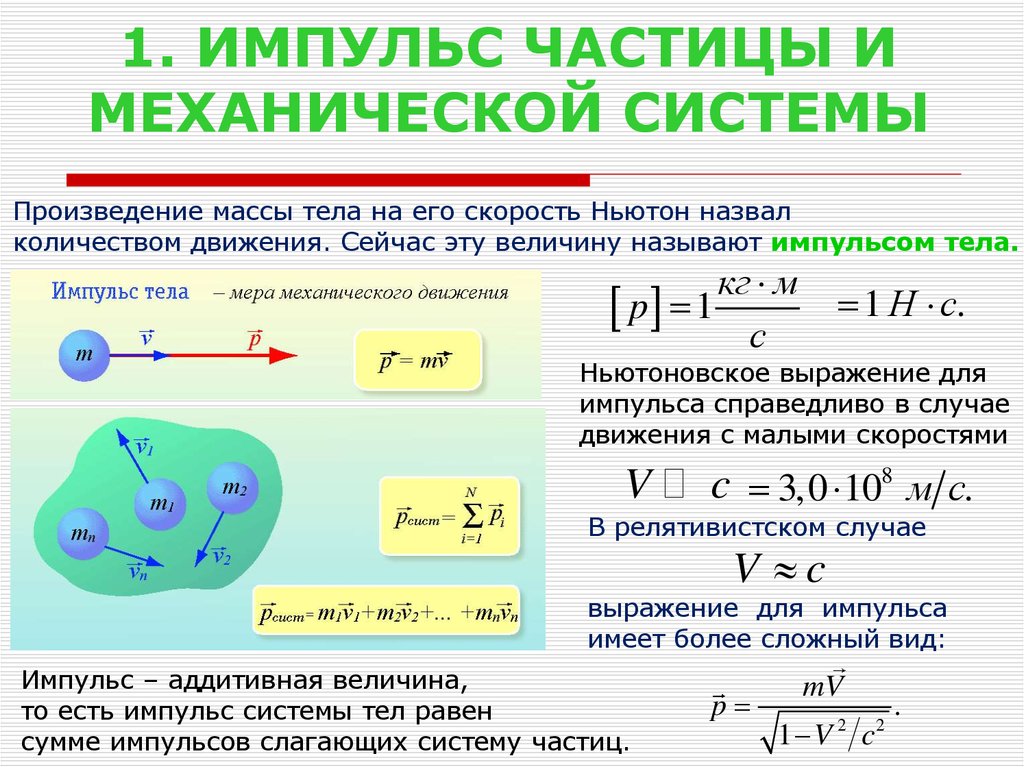 В ньютоновской физике импульс измеряется как произведение массы и составляющей скорости тела. Для безмассовых частиц (например, фотонов), движущихся со скоростью света (v = c), импульс ( p ) равен Постоянная Планка деленная на длину волны.
В ньютоновской физике импульс измеряется как произведение массы и составляющей скорости тела. Для безмассовых частиц (например, фотонов), движущихся со скоростью света (v = c), импульс ( p ) равен Постоянная Планка деленная на длину волны.
Первые формальные определения и измерения импульса относятся к работам французского философа Рене Декарта (1596–1650). Декарт подразумевал под импульсом поддающееся количественной оценке и измерению понятие, связанное с тем, что он назвал «количеством движения».
Измерение количества движения часто концентрируется на скорости изменения количества движения тел. В соответствии с законом инерции, тело без действующей на него суммарной силы не испытывает изменения импульса, и поэтому измерение импульса отражает сохранение импульса. Всякий раз, когда к телу прикладывается результирующая сила, изменение импульса пропорционально приложенной силе, но сохранение импульса диктует, что импульс агента, прилагающего силу к телу, должен соответственно уменьшаться, так что измеренный импульс объединенных систем остается неизменным. .
.
Современные устройства, используемые для измерения импульса субатомных частиц , часто используют устройства слежения, расположенные в сильных магнитных полях. Пути частиц, движущихся через эти поля, показывают их заряд и импульс. Направление отклонения показывает изменение частиц, и импульсы частиц можно рассчитать, исходя из того факта, что траектории частиц с большим импульсом отклоняются меньше, чем траектории с меньшим импульсом (т. пути).
Квантовая теория диктует, что измерение определенных пар свойств частиц, включая положение и импульс, ограничено принципом неопределенности Гейзенберга , впервые выдвинутым немецким физиком Вернером Гейзенбергом (1901-1976). В сущности, несмотря на то, что можно измерить либо положение, либо импульс, пара не может быть измерена одновременно. Чем точнее определение положения, тем более неопределенным становится измерение количества движения.
Хотя принцип неопределенности не применим к измерению импульса крупных объектов, он накладывает серьезные ограничения на измерения импульса субатомных частиц. Соответственно, квантовая теория накладывает ограничения на экспериментальное измерение импульса. Чем больше точность требуется при определении положения, тем меньше возможная точность в отношении определения импульса. Например, при попытке точно определить положение электронов необходимо бомбардировать электрон фотонами. При этом столкновения между фотонами и электроном изменяют импульс электрона и, следовательно, вносят неопределенность в измерение импульса электрона.
Соответственно, квантовая теория накладывает ограничения на экспериментальное измерение импульса. Чем больше точность требуется при определении положения, тем меньше возможная точность в отношении определения импульса. Например, при попытке точно определить положение электронов необходимо бомбардировать электрон фотонами. При этом столкновения между фотонами и электроном изменяют импульс электрона и, следовательно, вносят неопределенность в измерение импульса электрона.
Кроме того, существуют важные философские разветвления измерения импульса. Копенгагенская интерпретация квантовая механика реальность зависит от измерения наблюдателя. По сути, копенгагенская интерпретация диктует, что при измерении импульса или положения системы из двух частиц измерение импульса или положения одной частицы дает реальность импульсу или положению второй частицы. В этой теоретической интерпретации противоречивые реальности возникают при попытке измерить импульс одной частицы и положение другой. Поскольку временной порядок измерений зависит от инерциальной системы отсчета, различные системы отсчета дают разные реальности и порождают проблему нелокальности, связанную с мгновенным распространением информации, относящейся к измерению в реальном пространстве.
Поскольку временной порядок измерений зависит от инерциальной системы отсчета, различные системы отсчета дают разные реальности и порождают проблему нелокальности, связанную с мгновенным распространением информации, относящейся к измерению в реальном пространстве.
Импульс объекта равен массе объекта, умноженной на скорость объекта. Массу часто измеряют в килограммах (кг), а скорость — в метрах в секунду (м/с), поэтому импульс измеряют в килограммах метров в секунду (кг м/с). Поскольку скорость является векторной величиной, а это означает, что направление является частью величины, импульс также является вектором. Точно так же, как скорость, чтобы полностью указать импульс объекта, необходимо также указать направление.
Сила, умноженная на длину на , на которую действует сила, называется импульсом. Согласно теореме об импульсе импульса , импульс, действующий на объект, равен изменению импульса объекта. Обратите внимание на изменение слова. Импульс равен не импульсу объекта, а величине изменения импульса. (Эта теорема об импульсе импульса в основном представляет собой замаскированную форму второго закона Ньютона.) Сила, используемая здесь для определения импульса, представляет собой общую сумму всех внешних сил, действующих на объект. Внутренние силы, действующие внутри объекта, не учитываются.
(Эта теорема об импульсе импульса в основном представляет собой замаскированную форму второго закона Ньютона.) Сила, используемая здесь для определения импульса, представляет собой общую сумму всех внешних сил, действующих на объект. Внутренние силы, действующие внутри объекта, не учитываются.
Следствия этой теоремы об импульсе импульса довольно глубоки. Если на объект не действуют никакие внешние силы, то импульс (сила, умноженная на время) равен нулю . Изменение импульса также равно нулю, поскольку оно равно силе. Следовательно, если на объект не действуют внешние силы, импульс объекта никогда не может измениться. Этот закон есть закон сохранения импульса. Нет известных исключений из этого фундаментального закона физики. Как и другие закона сохранения (например, сохранение энергии ), закон сохранения количества движения является очень мощным инструментом для понимания Вселенной.
Что такое импульс и его единицы измерения
Выберите тип измерения: выберитеускорениеколичество веществауголплощадьемкостьданныеплотностьдинамическая вязкостьэлектромобиль энергия экономияэлектрический зарядэлектрический потенциалэлектрический потенциалэнергияэнтропиясилачастотарасход топливаиндудуктивностькинематическая вязкостьдлиналинейная плотностьинтенсивность светамагнитный потокплотность магнитного потокаимпульсчисломощностьдавлениерадиоактивность поглощенная дозарадиоактивностьскоростьвес плотность поверхноститемпературавремякрутящий моментобъем0017
Поиск единиц измерения:
5 единиц импульса — найдено.
Импульс p — векторная величина движения тела, которая определяется произведением его массы (m) на скорость ( v ): p = m × v Импульс направление совпадает со скоростью, т. е. с направлением движения тела. Метрическая единица импульса в системе СИ — килограмм-метр в секунду (кг⋅м/с).
В чем измеряется импульс? См. единицы измерения импульса и соответствующие им символы.
| О единице измерения | O: Преобразование единицы во все единицы T: Преобразование единицы в другую единицу измерения | |
|---|---|---|
| а.е. импульса | ℏ/a 0 | O:ℏ/a 0 T:ℏ/a 0 |
| gram centimeter per second | g⋅cm/s | O:g⋅cm/sT:g⋅cm/s |
| kilogram meter per second | kg⋅m/s | O:kg⋅m/sT:kg⋅m/s |
| ньютон-секунда | N⋅s | O:N⋅sT:N⋅s |
| слаг-фут в секунду 90899 9099 90 | O:sl⋅ft/sT:sl⋅ft/s |
- 1.
 Справочник по физике 1-е изд. 2002 Уолтер Бененсон, Джон В. Харрис, Хорст Стокер, Хольгер Лутц. Последнее обращение: 17 декабря 2020 г. (платная ссылка amazon.com).
Справочник по физике 1-е изд. 2002 Уолтер Бененсон, Джон В. Харрис, Хорст Стокер, Хольгер Лутц. Последнее обращение: 17 декабря 2020 г. (платная ссылка amazon.com).
продукты питания, питательные вещества и калории
шоколадные лаковые пончики для пирога, UPC: 011225114380 содержат (S) 403 калории на 100 грамм (≈3,53 унции) [цена]
1246 Foods, которые содержат Hydro). Список этих продуктов, начиная с самого высокого содержания гидроксипролина и самого низкого содержания гидроксипролина
Гравий, вещества и масла
CaribSea, Freshwater, Flora Max, Midnight весит 865 кг/м³ (54.00019фунт/фут³) с удельным весом 0,865 по отношению к чистой воде. Подсчитайте, сколько этого гравия требуется для достижения определенной глубины в цилиндрическом, четвертьцилиндрическом или прямоугольном аквариуме или пруду [вес к объему | объем к весу | цена ]
Оксид урана [UO 2 или O 2 U] весит 10 960 кг/м³ (684,21045 фунтов/фут³) [ вес к объему | объем к весу | цена | моль к объему и весу | масса и молярная концентрация | плотность ]
Преобразование объема в вес, веса в объем и стоимости для Хладагент R-417A, жидкий (R417A) с температурой в диапазоне от -30°C (-22°F) до 60°C (140°F)
Веса и измерения
Дина на квадратный дюйм — это единица давления, при которой сила в одну дин (дин) прикладывается к площади в один квадратный дюйм.

 Справочник по физике 1-е изд. 2002 Уолтер Бененсон, Джон В. Харрис, Хорст Стокер, Хольгер Лутц. Последнее обращение: 17 декабря 2020 г. (платная ссылка amazon.com).
Справочник по физике 1-е изд. 2002 Уолтер Бененсон, Джон В. Харрис, Хорст Стокер, Хольгер Лутц. Последнее обращение: 17 декабря 2020 г. (платная ссылка amazon.com).
Leave A Comment