Тест по геометрии Трапеция 8 класс с ответами

Тесты по геометрии 8 класс. Тема: «Трапеция»

Правильный вариант ответа отмечен знаком +

1. Среди представленных фигур нужно выбрать трапецию.

2. Среди данных определений указать верное для трапеции.

— многоугольник, который имеет попарно параллельные стороны, называется трапецией;

— четырёхугольник, у которого один из углов прямой, а две стороны равны, называется трапецией;

+ четырёхугольник, с двумя параллельными сторонами и двумя другими не параллельными, называется трапецией;

— многоугольник с равными сторонами именуется трапецией.

3. Какая фигура называется равнобедренной трапецией?

+ четырёхугольник, имеющий равные боковые не параллельные стороны;

— любая фигура с равными боковыми сторонами;

— четырёхугольник, который имеет боковые стороны, равные между собой;

— многоугольник, имеющий равные боковые стороны, параллельные друг другу.

4. Какие из названий сторон существуют для трапеции:

+ боковые и основания;

— боковые и средние;

— основания и вершины;

— вершины и боковые.

5. Если у трапеции имеется один прямой угол, то её называют:

— равнобедренной;

— параллельной;

— обычной;

+ прямоугольной.

6. Из представленных фигур требуется выбрать равнобедренную трапецию:

7. Даны несколько фигур. Какая из них является прямоугольной трапецией?

8. Какое свойство не справедливо для равнобедренной трапеции:

— углы при основании равны;

— диагонали равны;

— боковые стороны равны;

+ противолежащие углы равны.

9. Чему равна сумма углов трапеции?

— 2700;

+ 3600;

— 2500;

— 1800.

тест 10. Углы, прилежащие к любой боковой стороне, в сумме составляют:

— 2700;

— 3600;

— 2500;

+ 1800.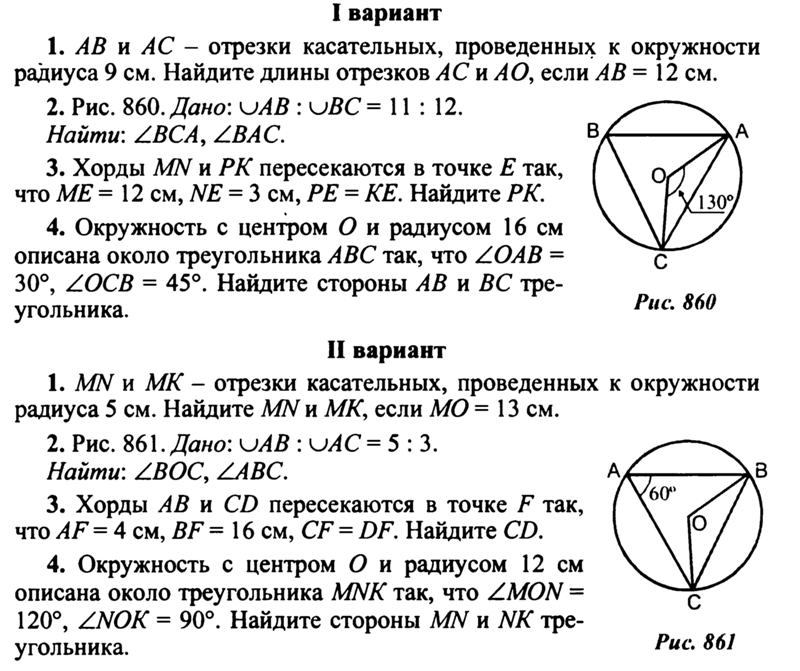

11. Дана трапеция SDFG. Угол S равен 350. Чему равен угол D?

+ 1450;

— 1500;

— 900;

— 350.

12. В трапеции ERTY известен угол T. Он равен 1180. Чему будет равен угол Y?

— 570;

— 620;

— 870;

+ 620.

13. Угол Е трапеции EBKC на 500 меньше угла В. Какое значение имеет угол В?

+ 1150;

— 2300;

— 1870;

— 1620.

14. Угол В трапеции EBKC на 500 больше угла Е. Какое значение имеет угол Е?

— 670;

— 450;

— 850;

+ 650.

15. Дана трапеция. Угол Е=30°, KH – высота, проведённая к ED. Чему будет равна EK?

— 20;

+ 18;

— 22;

— 35.

16. Дана равнобедренная трапеция YKPR. Основание KP=12, высота KH=10, угол Y= 30°. Где не допущена ошибка в решении, при нахождении основания YR?

+ а) YK=2×KH=2×10=20

Yh3=202-102=400-100=300

YH=√300=10√3

YR=2×10√3+12=12+20√3;

— b) YK=KH=10

Yh3=102+102=200

YH=√200=10√2

YR=2×10√2+12=12+20√2;

— c) YK=2×KH=2×10=20

Yh3=202-102=400-100=300

YH=√300=10√3

YR=10√3+12=12+10√3;

— d) YK=2×KH=2×10=20

Yh3=202-102=400

YH=√400=20

YR=2×20+12=412.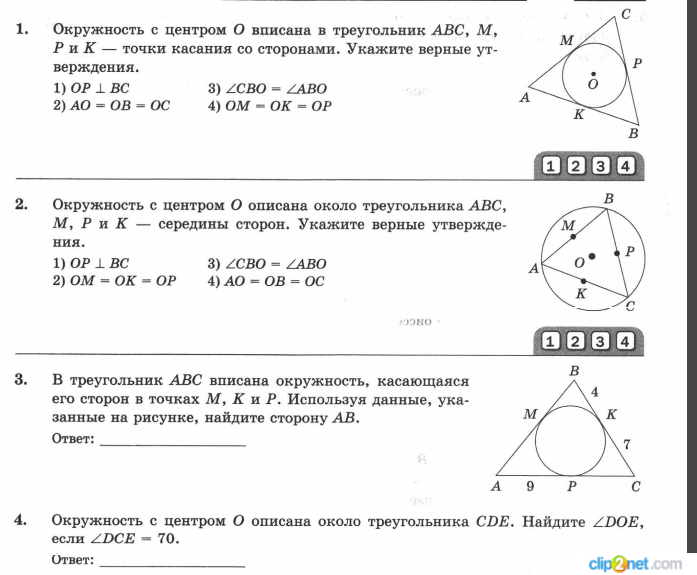

17. В равнобедренной трапеции YKPR основание KP =12, высота PQ=10, угол R=60°. Какой из представленных вариантов нахождения основания YR верный?

— а) QR= PR

QR=x, PR=x

x2=x2+102

x2+x2=102

2×2=100

x2=50

x=5√2

YR=2×5√2+12=10√2+12;

— b) QR=1/2 PR

QR=x, PR=2x

4×2=x2+102

4×2+x2=102

5×2=100

x2=20

x=2√5

YR=2×2√5+12=4√5+12;

— c) QR=1/2 PR

QR=x, PR=2x

4×2=x2+102

4×2-x2=102

3×2=100

x2=100/3

x=√100/3=10√3

YR=2×10√3+12=20√3+12;

+ d) QR=1/2 PR

QR=x, PR=2x

4×2=x2+102

4×2-x2=102

3×2=100

x2=100/3

x=√100/3=10/3√3

YR=2×10/3√3+12=20/3√3+12.

18. Дан угол 68° в равнобедренной трапеции. Остальные углы равны:

+112° и 68°;

-112°, 68°, 115° и 65°;

— 112°,68°, 90° и 90°;

— 111° и 69°.

19. В прямоугольной трапеции KBDH диагональ KD образует угол KDH=90°, основание BD=10, высота DO=9, угол H = 45°. Каково значение KH?

— 20;

— 23;

+ 19;

— 21.

тест-20. Чего не может быть в прямоугольной трапеции?

— двух прямых углов;

— двух прямых углов, одного острого и одного тупого;

+двух острых углов;

— двух одинаковых углов.

21. Высота прямоугольной трапеции равна:

+ меньшей боковой стороне;

— большей боковой стороне;

— идентична основанию;

— совпадает с диагональю.

22. На какие фигуры делит прямоугольную трапецию высота, проведённая из вершины тупого угла?

— на два равных треугольника;

— на квадрат и ромб;

+ на прямоугольный треугольник и прямоугольник;

— на прямоугольный треугольник и равнобедренный треугольник.

23. Дана равнобедренная трапеция с большим основанием 7 см. Меньшее основание составляет 5 см. Углы при большем основании равны 60°. Найти боковую сторону.

— 1 см;

— 3 см;

— 1,5 см;

+ 2 см.

24. В равнобедренной трапеции угол при меньшем основании равен 135°. Большее и меньшее основание 18 и 10. Найти высоту трапеции.

+4;

— 8;

— 12;

— 2.

25. В прямоугольной трапеции острый угол равен 45°. Высота равна меньшему основанию и составляет 15 см. Чему будет равняться большее основание?

+ 30;

— 15;

— 45;

— 50.

26. Как называется отрезок, проходящий через середины боковых сторон трапеции, параллельный основаниям?

— основная линия трапеции;

+ средняя линия трапеции;

— средняя линия треугольника;

— половинная линия трапеции.

27. Средняя линия трапеции равна…

— полусумме основания, умноженного на высоту;

+ полусумме оснований;

— сумме оснований;

— без рисунка сказать это невозможно.

28. В трапеции нужно найти отрезок, соединяющий середины боковых сторон. При этом известны значения меньшего основания — 6, и большего основания — 14.

+10;

— 20;

— 14;

— 7.

29. Дана средняя линия трапеции. Её значение равно 30. Большее основание равно 45. Чему равно меньшее основание?

— 20;

— 40;

— 30;

+ 15.

тест_30. В равнобедренной трапеции из вершины тупого угла к большему основанию опущен перпендикуляр. Он делит его на отрезки равные 10 см и 4 см. Найти среднюю линию трапеции.

+ 8;

— 10;

— 7;

— 6.

Тест: Трапеция. Вариант 1. — Математика 8 класс

Тест: Трапеция. Вариант 1. — Математика 8 класс

Английский язык

Астрономия

Белорусский язык

Биология

География

ИЗО

Информатика

История

Итальянский язык

Краеведение

Литература

Математика

Музыка

Немецкий язык

ОБЖ

Обществознание

Окружающий мир

ОРКСЭ

Русский язык

Технология

Физика

Физкультура

Химия

Черчение

Для учителей

Дошкольникам

VIP — доступ

  • Предметы
    • »
  • Математика
    • »
  • 8 класс
    • »
  • Трапеция. Вариант 1.

Трапеция. Вариант 1.

Проверка знаний и навыков

Математика 8 класс | Автор: Ахметова Резеда Ильдусовна | ID: 2687 | Дата: 18.7.2014

Помещать страницу в закладки могут только зарегистрированные пользователи

Зарегистрироваться

Вопрос № 1

А1. В трапеции ABCD основани равны 8 см и 14 см .Чему равна ее средняя линия?

22 см
7 см
11 см
6 см

Вопрос № 2

А2. В трапеции ABCD угол А=37 градусов, угол С=126 градусов. Чему равна сумма мер углом B и D?

163
269
91
197

Вопрос № 3

А3. В трапеции ABCD из вершины угла B проведена прямая, параллельная стороне CD и пересекающая сторону AD в точке E так что угол АBE=75.

угол А=40.Чему равен угол CBE?

65
75
40
115

Вопрос № 4

А4. В равнобедренной трапеции угол при основании раыен 60°, а основания равны 6 и 10 см. Чему равен периметр трапеции?

28
26
20
24

Вопрос № 5

В1. В трапеции ABCD AD и BC-основания, AD>BC. На стороне AD отмечена точка К так, что KBCD-параллелограмм. Периметр треугольника ABK равен 25 см, DK=6cм. Найдите периметр трапеции

Введите ответ:

Вопрос № 6

В2. В равнобедренной трапеции ABCD диагональ AC перпендикулярна боковой стороне, угол D=60*, AD=20 см, BC=10 см. Найдите периметр трапеции.

Введите ответ:

Вопрос № 7

С1.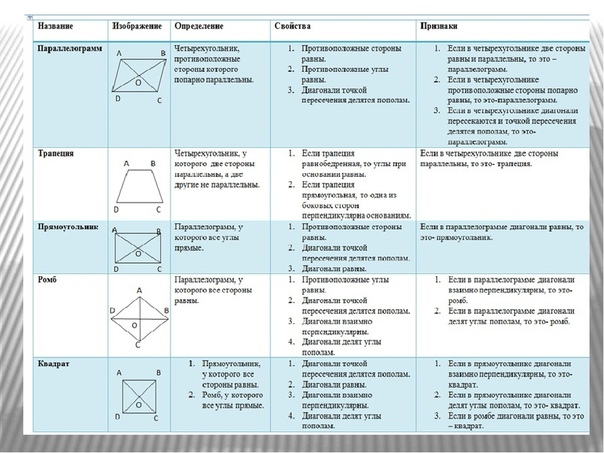

В прямоугольной трапеции острый угол и угол который составляет меньшая диагональ с меньшем основанием равны по 60°. Найдите отношение оснований.

Введите ответ:

Показать ответы

Получение сертификата
о прохождении теста

Доступно только зарегистрированным пользователям

© TestEdu.ru 2013-2022

E-mail администратора: [email protected]

Трапеции — Количественный анализ верхнего уровня ISEE

Все ресурсы количественного анализа верхнего уровня ISEE

8 Диагностические тесты 234 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

Количественная помощь верхнего уровня ISEE » Геометрия » Плоская геометрия » Четырехугольники » Трапеции

Какая величина больше?

(a) Периметр вышеуказанной трапеции

(b) Периметр прямоугольника с длиной и шириной  и соответственно.

Возможные ответы:

(б) больше

Из предоставленной информации невозможно определить, что больше

(а) больше

(а) и (б) равны

Правильный ответ:

(а) больше

Объяснение:

Периметр прямоугольника равен удвоенной сумме его длины и ширины:

Поскольку высота трапеции на рисунке равна , обе ее стороны должны иметь длину больше или равную . Но чтобы катет имел длину, он должен быть перпендикулярен основаниям. Поскольку перпендикулярность обоих катетов сделала бы трапецию прямоугольником, чего быть не может, отсюда следует, что оба катета не могут иметь длины. Следовательно, периметр трапеции равен:

Периметр трапеции должен быть больше периметра прямоугольника.

Сообщить об ошибке

Рисунок выполнен НЕ в масштабе.

На приведенном выше рисунке это середина равнобедренной трапеции.

Также, .

Каков периметр трапеции  ?

Возможные ответы:

Правильный ответ:

Объяснение:

Длина среднего сегмента трапеции равна половине суммы длин оснований, поэтому

.

Кроме того, по определению, поскольку трапеция  равнобедренная, . Средний сегмент делит обе стороны трапеции на конгруэнтные сегменты; объединяя эти факты:

.

, поэтому периметр трапеции равен

.

Сообщить об ошибке

На приведенном выше рисунке это середина трапеции.

Какое количество больше?

(a) Удвоенный периметр трапеции

(b) Периметр трапеции

Возможные ответы:

(б) — большее количество

(а) — большее количество

Из предоставленной информации невозможно определить, что больше

(а) и (б) равны

Правильный ответ:

(а) больше

Пояснение:

Средняя часть трапеции делит обе стороны пополам, поэтому

  и  .

По причинам, которые станут очевидны позже, мы установим

Также длина средней части равна половине суммы длин оснований:

.

Периметр трапеции равен

В два раза больше

Периметр трапеции равен

, что делает (a) большее количество.

Сообщить об ошибке

Трапеция A и параллелограмм B имеют одинаковую высоту. Трапеция А имеет основания 10 и 16; Параллелограмм B имеет основание 13. Какая величина больше?

(a) Площадь трапеции A

(b) Площадь параллелограмма B

Возможные ответы:

(a) и (b) равны.

(а) больше.

(б) больше.

По предоставленной информации сказать невозможно.

Правильный ответ:

(a) и (b) равны.

Объяснение:

Пусть будет общая высота фигур.

(a) Площадь трапеции A равна .

(b) Площадь параллелограмма B равна

.

Фигуры имеют одинаковую площадь.

Сообщить об ошибке

На параллелограмме, , найдите точку на так, чтобы ; найдите точку  на  так, чтобы . Рисовать .

Какое количество больше?

(а) Площадь четырехугольника

(б) Площадь четырехугольника

Возможные ответы:

(а) и (б) равны

(а) больше

Невозможно сказать из предоставленной информации

(б) больше

Правильный ответ:

(а) больше

Объяснение:

 делит параллелограмм на две трапеции, каждая из которых имеет ту же высоту, что и исходный параллелограмм, который мы будем называть .

(a) Основаниями трапеции  являются  и .

(b) Основания трапеции  равны и .

Противоположные стороны параллелограмма конгруэнтны, так как ,  тоже.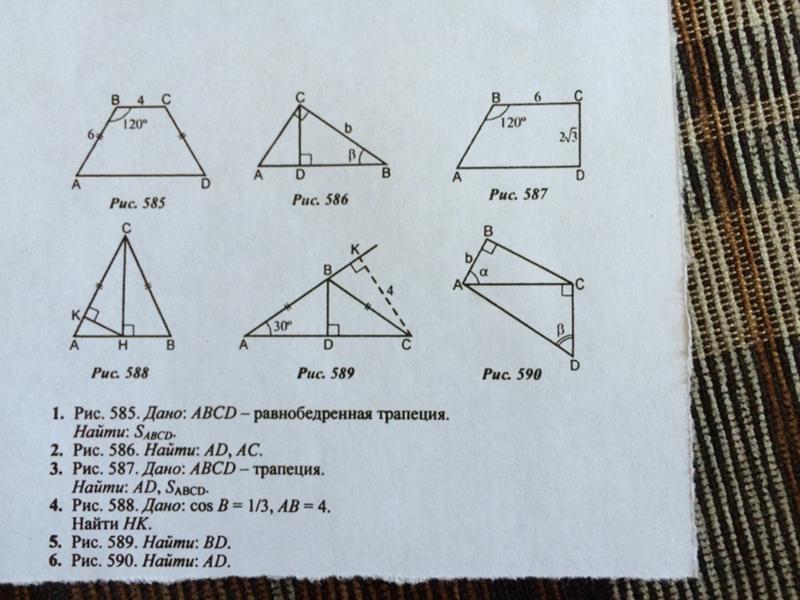

Сумма оснований трапеции А равна 21; сумма трапеций B равна 19. Две трапеции имеют одинаковую высоту. Следовательно, поскольку площадь равна половине высоты, умноженной на сумму оснований, трапеция А будет иметь большую площадь.

Сообщить об ошибке

Какое количество больше?

(a) Площадь трапеции с основаниями 75 сантиметров и 85 сантиметров и высотой один метр.

(b) Площадь параллелограмма с основанием 8 дм и высотой 1 м.

Возможные ответы:

(b) больше.

(а) больше.

(а) и (б) равны.

По предоставленной информации сказать невозможно.

Правильный ответ:

(a) и (b) равны.

Объяснение:

Самый простой способ сравнения — преобразовать каждую меру в сантиметры и вычислить площади в квадратных сантиметрах. Обе фигуры имеют высоту один метр, или 100 сантиметров.

(a) Подставьте  в формулу площади:

‘

 квадратные сантиметры

 

(b) 8 дециметров равно 100 сантиметров высоты на 80, поэтому

 квадратных сантиметров

Фигуры имеют одинаковую площадь.

Сообщить об ошибке

Какое количество больше?

(a) Площадь трапеции с основаниями в футах и ​​футах и ​​высотой в один ярд.

(b) Площадь параллелограмма с основанием в футах и ​​высотой в один ярд.

Возможные ответы:

По предоставленной информации сказать невозможно.

(а) и (б) равны.

(а) больше.

(б) больше.

Правильный ответ:

(а) больше.

Объяснение:

Самый простой способ сравнить площади — преобразовать каждое из измерений в дюймы.

(a) Основания преобразуются путем умножения числа футов на двенадцать; высота составляет один ярд, что составляет 36 дюймов.

дюйма

дюйма

Заместитель в формулу для площади трапеции, настройка:

квадратных дюймов

(b) Основание параллелограммы составляет

.

Умножьте это на высоту:

 квадратных дюймов

 

Трапеция имеет большую площадь.

 

Сообщить об ошибке

Какое количество больше?

(a) Площадь указанной выше трапеции

(b) Площадь квадрата со сторонами длины

Возможные ответы:

(b) — большее количество

(a) — большее количество

Из приведенной информации невозможно определить, что больше

(а) и (б) равны

Правильный ответ:

(b) большее количество

Объяснение:

Площадь трапеции равна половине произведения ее высоты, которая здесь равна , и суммы длин ее оснований, которые здесь равны и : квадрата – это квадрат длины стороны, которая здесь равна:

 

Квадрат имеет большую площадь.

Сообщить об ошибке

Какое количество больше?

(a) Площадь указанной трапеции

(b) Площадь квадрата с диагоналями длины 

Возможные ответы:

(a) больше

Невозможно определить, какая из больше из приведенной информации

(a) и (b) равны

(b) больше

Правильный ответ:

(a) и (b) равны

Объяснение:

Площадь трапеции равна половине произведения ее высоты, которая здесь равна , и суммы длин ее оснований, которые здесь равны и : квадрат, будучи ромбом, составляет половину произведения длин его диагоналей, обе из которых здесь:

Трапеция и квадрат имеют одинаковую площадь.

Сообщить об ошибке

На приведенном выше рисунке это середина трапеции. Какой процент трапеции был затенен?

Возможные ответы:

Правильный ответ:

Пояснение:

Середина сегмента  делит трапецию  на две трапеции одинаковой высоты, которые мы будем называть ; длина среднего сегмента равна половине суммы длин оснований:

Площадь трапеции равна половине произведения ее высоты на сумму длин ее оснований. Следовательно, площадь Трапеции  — заштрихованной трапеции — 

Площадь трапеции составляет

Процент трапеции, который заштрихован

Отчет о ошибке

work All 1 Уровень Количественные ресурсы

8 Диагностические тесты 234 практических теста Вопрос дня Карточки Learn by Concept

Трапеции: примеры, формулы и характеристики

Что общего между китайской коробкой на вынос и дизайнерской сумочкой? Обратите внимание, как они представляют одну и ту же форму.

Форма параллелограмма сумки и коробки для еды на вынос, StudySmarter Originals

Теперь обратите внимание на то, что основания сумки и коробки для еды на вынос параллельны их вершинам. Поскольку эта фигура имеет четыре стороны, она классифицируется как тип четырехугольника. Однако это не квадрат, не прямоугольник и не параллелограмм. Эти формы имеют две пары параллельных сторон, в то время как форма, описанная этой сумкой и коробкой на вынос, имеет только одну пару. Есть ли у вас какие-либо предположения относительно того, какой может быть эта форма? Даю подсказку: это называется трапеция.

В этой статье будет рассмотрено определение трапеции, а также ее характеристики и типы. Мы также рассмотрим формулы, используемые для нахождения периметра и площади трапеции.

Что такое трапеция?

Как упоминалось ранее, трапеция подпадает под категорию четырехугольника, поскольку она содержит четыре стороны. Этот особый тип четырехугольника на самом деле имеет два названия: трапеция и трапеция. Имя зависит от того, где вы находитесь в мире. Здесь, в Соединенных Штатах, его обычно называют трапецией. Однако в Соединенном Королевстве ее обычно называют трапецией. Насколько это интересно? Имея это в виду, давайте начнем наше обсуждение с определения трапеции.

Трапеция представляет собой четырехугольник с одним набором параллельных сторон.

Ниже приведено графическое изображение трапеции. Назовем эту трапецию ABCD.

Иллюстрация трапеции, StudySmarter Originals

Теперь перейдем к перечислению свойств трапеции. Таким образом, мы можем наблюдать, насколько они отличаются от правильного четырехугольника.

Характеристики трапеции

Теперь вернемся к нашей трапеции ABCD выше. Есть несколько примечательных характеристик трапеций, с которыми нам следует ознакомиться. Они перечислены ниже.

  • Трапеция имеет пару параллельных сторон и пару непараллельных сторон;

  • Обычно основания (верхнее и нижнее) треугольника ABCD параллельны друг другу. Это можно записать как AD//BC;

По определению трапеции.

  • Пара смежных углов, образованных между одной параллельной и одной непараллельной стороной трапеции, в сумме составляет 180°. Здесь ∠ABC + ∠BAD = 180° и ∠BCD + ∠ADC = 180°;

  • Сумма внутренних углов трапеции равна 360°;

  • Диагонали трапеции делят друг друга пополам;

  • Медиана (средняя линия или средний сегмент) трапеции параллельна обоим основаниям. Это показано розовой линией ниже;

Медиана трапеции, StudySmarter Originals

Медиана (или середина) трапеции — это отрезок, соединяющий середины двух непараллельных сторон трапеции.

Составление других четырехугольников из трапеций

Существует три типа четырехугольников, которые могут быть получены из трапеций, а именно параллелограмм, квадрат и прямоугольник. Эти экземпляры описаны в таблице ниже.

Type of Quadrilateral

Description

Parallelogram

Parallelogram, StudySmarter Originals

квадрат

квадрат, StudySmarter Originals

.

  1. Разносторонняя трапеция

  2. Равнобедренная трапеция

  3. Правая трапеция

  4. Тупая трапеция

  5. Острая трапеция

В приведенной ниже таблице по очереди описывается каждая из этих трапеций, а также их графическое изображение и отличительные черты.

Type of Trapezoid

Pictorial Representation

Description

Scalene Trapezoid

Scalene trapezoid, StudySmarter Originals

Трапеция без равных сторон и углов.

Равнобедренная трапеция

Равнобедренная трапеция, StudySmarter Originals

Трапеция с противоположными сторонами одинаковой длины.

Обычно представляют собой непараллельные стороны (или катеты) трапеции. Углы параллельных сторон (или оснований) равны друг другу.

Правая трапеция

Прямоугольная трапеция, StudySmarter Originals

Трапеция с двумя смежными прямыми углами (равными 90 o ).

Тупой трапециевид

Тупкий трапециэприз, StudySmarter Originals

Трапезоид с двумя противоположными угловыми наглавыми (более 94949494949 40004.

Острая трапеция

Острая трапеция, StudySmarter Originals

Трапеция с двумя соседними острыми углами (менее 90 o ).

Периметр трапеции

Трапеция — это двумерный многоугольник, лежащий на двумерной плоскости. Периметр трапеции описывается как общая длина ее границы. Другими словами, это сумма всех его сторон. Допустим, у нас есть трапеция ABCD со сторонами a, b, c и d.

Периметр трапеции, StudySmarter Originals

Тогда формула периметра трапеции равна

P = a + b + c + d,

, где P — периметр, a = AB, b = BC, c = CD и d = AD. Это также можно записать как

P = AB + BC + CD + AD.

Примеры с использованием формулы периметра трапеции

Давайте теперь рассмотрим некоторые рабочие примеры, использующие формулу для нахождения периметра трапеции.

Дана трапеция ниже, найдите ее периметр.

Пример 1, StudySmarter Originals

Решение

Чтобы найти периметр этой трапеции, мы просто сложим измерения всех четырех сторон вместе.

P=13+21+19+34⇒P=87единиц

Таким образом, периметр этой трапеции равен 87 единицам.

Периметр равнобедренной трапеции равен 35 единицам. Какова длина каждой (равной) противоположной стороны, если основания равны 5 единицам и 8 единицам соответственно?

Решение

Здесь нам дан периметр трапеции и длины оснований. Нам также говорят, что эта трапеция является равнобедренной трапецией, а это означает, что у нее есть пара равных противоположных сторон. Мы будем называть эти две одинаковые стороны через х.

Пример 2, StudySmarter Originals

Поскольку периметр представляет собой сумму всех четырех сторон этой трапеции, мы можем записать это уравнение в виде приведенного ниже уравнения.

P=5+8+x+x⇒35=13+2x

Преобразовывая это уравнение, получаем

2x=35-13⇒2x=22

Упрощая, получаем

x=222⇒x=11единиц

Таким образом, стоимость каждой противоположной стороны равна 11 единицам.

Площадь трапеции

Площадь трапеции определяется пространством, заключенным внутри ее границы. Его находят путем вычисления средней длины между двумя заданными параллельными сторонами и умножения этого произведения на высоту трапеции. Обратите внимание на рисунок трапеции ABCD ниже.

Площадь трапеции, StudySmarter Originals

Здесь основания равны a = BC и b = AD. Высота обозначается буквой h.

Высота h трапеции находится на перпендикулярном расстоянии между основаниями a и b. Его также называют высотой трапеции.

Таким образом, площадь трапеции равна

A=12(a+b)×h ,

, где A = площадь, a = длина более короткого основания, b = длина более длинного основания и h = высота. Точно так же мы можем выразить эту формулу как

A=BC+AD2×ч.

Примеры с использованием формулы площади трапеции

Давайте теперь посмотрим на некоторые рабочие примеры с применением формулы площади трапеции.

Определите площадь следующей трапеции.

Пример 3, StudySmarter Originals

Solution

Здесь

a = 6 единиц;

б = 8 шт.;

ч = 5 шт.

Пусть вас не смущают две другие стороны! Они не параллельны друг другу, поэтому мы не можем использовать их меры в нашей формуле.

Теперь, используя формулу площади трапеции, получаем

A=12(a+b)×h⇒A=12(6+8)×5

Упрощая это, мы получаем окончательный ответ

A=12(14)×5⇒A=7×5⇒A=35единиц2

Таким образом, площадь этой трапеции равна 35 единицам 2 .

Найдите длину меньшего основания трапеции, зная, что площадь равна 232 единицам 2 , высота равна 16 единицам, а длина большего основания равна 17 единицам.

Раствор

В этом случае

A = 232 единицы 2

b = 17 единиц;

ч = 16 шт.

Подставив эти значения в нашу формулу, получим

A=12(a+b)×h⇒232=12(a+17)×16

Решив это, получим

232=16(a+17 )2⇒232=8(a+17)

Расширяя это, мы получаем

232=8a+136⇒8a+136=232

Преобразовывая это уравнение и решая для a, мы получаем следующий окончательный ответ.

8а=232-136⇒8а=96⇒а=968⇒a=12единиц

Следовательно, длина меньшего основания этой трапеции равна 12 единицам.

Пример с участием трапеций

Мы закончим эту тему примером, который охватывает все, что мы узнали в ходе этого обсуждения.

Дана трапеция ABCD ниже, определите ее тип, периметр и площадь.

Пример 4, StudySmarter Originals

Решение

Тип

Сначала выясним, какой это тип трапеции. Глядя на диаграмму выше, обратите внимание, что ∠BAD = 103 о и ∠BCD = 118 о . Оба эти угла больше 90 o и расположены друг напротив друга. Таким образом, у нас получилась тупая трапеция.

Периметр

Далее найдем периметр этой трапеции. Складывая все четыре стороны этой трапеции, получаем

P=AB+BC+CD+AD⇒P=14+16+18+22⇒P=70единиц

Таким образом, периметр этой трапеции равен 70 единицам.

Площадь

Здесь BC (более короткое основание) параллельно AD (более длинное основание). Высота перпендикулярна обоим этим основаниям. Таким образом,

а = 16 шт.;

б = 22 шт.;

ч = 11 шт.

Применяя формулу площади трапеции, получаем

A=12(16+22)×11⇒A=12(38)×11⇒A=19×11⇒A=209единиц2

Таким образом, площадь этой трапеции равна 209 единиц 2 .

Дополнительный вопрос

Чему равно значение угла ∠ADC, если ∠ABC = 88 o ?

По свойству трапеций сумма внутренних углов равна 360°. Поскольку у нас есть меры трех углов, мы можем найти значение недостающего угла ниже.

∠ABC+∠BCD+∠ADC+∠BAD=360°⇒88°+118°+∠ADC+103°==360°

Переставляя это и решая для неизвестного угла, мы получаем

∠ADC=360°- 88°-118°-103°⇒∠ADC=51°

Таким образом, угол ∠ADC равен 51 o .

Трапеции — основные выводы