Найти наименьшее и наибольшее значение функции y: Нахождение наибольшего и наименьшего значения функции — пример

Нахождение наибольшего и наименьшего значения функции — пример

В этой статье мы разберём нахождение наибольшего и наименьшего значения функции на отрезке, интервале, в бесконечности, а также повторим основные свойства функции и связанные термины.

Что такое функция

Наш мир — это огромная коллекция взаимосвязей, которые порой явно, а порой невидимо влияют на всех, кто в них участвует. Ваше настроение может влиять на успеваемость в школе, питание — на спортивные достижения, навыки — на возможность поступить в университет. В физическом мире температура влияет на скорость протекания процесса, плотность тела — на его способность к плаванию в воде, угол падения лучей — на то, каким образом они будут преломляться, пройдя через прозрачную призму.

Некоторые из этих взаимоотношений можно описать математически: обозначить участников буквами латинского алфавита и описать их взаимосвязь через математические действия и знаки.

Функция — это правило, формула или выражение, которое описывает взаимосвязь двух величин.

Как описать зависимость пройденного пути от времени?

Есть ли правило, которое описывает отношение ускорения тела и силы, приложенной к нему? Да:

А что, если нужно вычислить зависимость остатка денег от количества купленных товаров? Пожалуйста:

, где

— остаток денег,

— исходная сумма,

— количество товара,

— стоимость товара за одну единицу.

В каждом из этих выражений есть зависимая и независимая переменные. Зависимая переменная — это и есть функция, а независимая — аргумент. Так, в нашем последнем примере стоимость товара за одну его единицу является независимой переменной (цену назначил продавец, и мы на это повлиять никак не можем). Зато остаток в кошельке поддаётся изменениям — чем меньше мы купим товара, тем больше останется денег. И так в любой зависимости!

Обратите внимание

Зависимая переменная стоит слева от знака «равно» и определяется через выражение, содержащее аргумент.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Графическое задание функции

Представьте, что для школьной научной конференции вы готовите доклад о загрязнении окружающей среды. Как вы думаете, что произведёт больший эффект на аудиторию:

Верно — иллюстрации, фотографии, графики и диаграммы говорят порой громче любых слов! 📈

Для наглядного отображения зависимости одной переменной от другой мы введём систему координат, в которой построим график.

График — это прямая, кривая или ломаная линия, которая была построена чётко по уравнению (функции).

Как мы уже говорили, функция состоит из зависимой и независимой переменной. В декартовой системе координат независимая переменная отображается с помощью оси зависимая — с помощью оси

В зависимости от типа функции график может выглядеть, например, так:

Наибольшее и наименьшее значение функции

На уроках алгебры учитель просит определить наибольшее и наименьшее значение функции. Что он имеет в виду?

Чтобы найти наименьшее или наибольшее значение функции, необходимо понять, какое наименьшее или наибольшее численное значение принимает — зависимая переменная.

Наибольшее значение функции на некотором промежутке — это значение которое при любом значении делает справедливым неравенство

Теперь расшифровка! 😅 Если на данном интервале значение больше, чем значение в окрестностях точки то такой будет считаться наибольшим значением на данном промежутке.

Наименьшее значение функции на некотором промежутке — это значение которое при любом значении делает справедливым неравенство

Если на данном интервале значение меньше, чем значение в окрестностях точки то такой будет считаться наименьшим значением на данном промежутке.

Наибольшее и наименьшее значение функции на графиках

Самый простой способ определить и — рассмотреть график.

Если заданный интервал представлен прямой:

• при возрастающей функции: наименьшее значение функция примет при наименьшем аргументе и наоборот, наибольшее значение функции будет соответствовать наибольшему значению аргумента;

• при убывающей функции: наименьшее значение функция примет при наибольшем аргументе и наоборот, наибольшее значение функции будет соответствовать наименьшему значению аргумента.

Если заданный интервал представлен кривой:

• максимальное значение функции выглядит как вершина горы, возвышенности, тогда как минимальное значение мы можем определить как самую низкую точку относительно этого пика;

• минимальное значение функции выглядит как дно низины, оврага, тогда как максимальное значение мы можем определить как самую высокую точку относительно этого пика.

Возможен и такой вариант, когда горы и овраги встречаются на одном промежутке — тогда мы просто объединяем оба пункта для нахождения и Помним главное правило: максимальное значение функции всегда представлено самой высокой точкой относительно оси минимальное значение функции — самой низкой точкой.

Определение наименьшего и наибольшего значения через производную

Удобен ли способ нахождения и через график? Определённо! Всегда ли его можно использовать? К сожалению, нет.

Дело в том, что большинство заданий в алгебре на эту тему даются не через график, а через уравнение функции. Зачастую эти функции сложные, и построение их графиков займёт время. Ошибётесь в построении — допустите ошибку и в нахождении максимального и минимального значения, а нам это не нужно.

Способ, который не уступает первому в простоте и лаконичности, заключается в определении производной функции и поиске стационарных точек. Кажется, нам встретились два новых термина — давайте их разберём.

Производная функции — это отношение приращения функции к приращению аргумента при бесконечно малом приращении аргумента.

Производная функции показывает, как быстро увеличивается функция при бесконечно малом увеличении

По сути, найти производную означает провести определённые действия с помощью таблицы производных функций.

Обязательно загляните в нашу статью об этом и изучите материал, а мы пока пойдём дальше.

Стационарная точка — точка, в которой значение аргумента производной функции равно нулю.

Дело в том, что по теореме Ферма в стационарных точках определяется экстремум функции, поэтому можно сделать вывод, что на некотором промежутке в них можно определить и наибольшее/наименьшее значение функции.

Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке

Как определить наибольшее и наименьшее значения функции на отрезке?

1. Найдём область определения данной функции и проверим, входит ли в неё заданный отрезок.

2. Найдём производную данной функции.

3. Приравняем производную к нулю и найдём точки, в которых она обращается в нуль (решим уравнение).

4. Выберем из корней уравнения те точки, которые попадают в заданный промежуток, и вычислим значение функции в них.

5. Возьмём точки начала и конца отрезка и найдём значение функции в них.

6. Сделаем вывод о наибольшем и наименьшем значении функции.

Разберём пару примеров.

Задача 1

Найдите наибольшее и наименьшее значение функции на отрезке

Решение:

1. ОДЗ:

4. не попадает в промежуток Найдём значение функции только в крайних точках:

5. Тогда является наименьшим значением на данном отрезке, а наибольшим.

Задача 2

Найдите наибольшее и наименьшее значение функции на отрезке

Решение:

1. ОДЗ:

3. , но в таком случае знаменатель равен нулю, что невозможно. А значит, производная не обращается в нуль, стационарных точек нет.

4. Найдём значение функции в крайних точках отрезка:

   — точка максимума на промежутке;

   — точка минимума на промежутке.

Наименьшее и наибольшее значение функции на открытом или бесконечном интервале

В чём отличие отрезка от интервала? В отрезке определены крайние точки, в интервале же крайние точки могут не существовать (например ), или значение функции в них мы рассматривать не будем (на интервале мы рассмотрим значение функции в окрестностях этих точек, но не в них самих).

Вариантов задания интервала может быть множество, но каждый из них сведёт определение и к поиску производной и вычислению пределов в крайних точках, например и

Вернёмся на пару шагов назад. А что такое предел функции?

Если говорить коротко, то предел функции — это такое число , к которому функция стремится, в то время как аргумент стремится достичь числа

Предположим, наша функция представлена уравнением Найдём предел функции при подставив это значение вместо в уравнение:

Это означает, что функция стремится приблизиться к числу в то время как аргумент тоже приближается к этому значению. В отрыве от настоящего уравнения мы могли бы представить это так:

Функция может стремиться не только к рациональному числу, но также и к бесконечности. В таком случае при подстановке бесконечности в функцию возникает неопределённость, которую необходимо решить разными методами.

В рамках этой статьи мы не можем посвятить этому много времени, поэтому ждём Вас на курсах математики в онлайн-школе Skysmart — там ни один предел не останется незамеченным. 😉

Вернёмся к функции! Итак, как же определить наибольшее и наименьшее значение на интервале?

1. Найдём область определения данной функции и проверим, входит ли в неё заданный интервал.

2. Найдём производную данной функции.

3. Приравняем производную к нулю и найдём точки, в которых она обращается в нуль (решим уравнение).

4. Выберем из корней уравнения те точки, которые попадают в заданный промежуток, и вычислим значение функции в них.

5. Возьмём крайние точки интервала и вычислим значение предела в этих точках (согласно типу интервала).

6. Сделаем вывод о наибольшем и наименьшем значении функции.

Для вычисления предела вам поможет сводная таблица, которая учитывает вид интервала:

Интервал	Предел
	и
	и
	и

Если при вычислении одностороннего предела вы получаете бесконечность, то вычислить наибольшее/наименьшее значение невозможно.

Задача 3

Необходимо найти наибольшее и наименьшее значение функции на всём промежутке области определения.

Решение:

1. ОДЗ:

3. Найдём стационарные точки:

4. Точка входит в промежуток области определения и является точкой минимума.

5. Так как — парабола, ветви которой направлены вверх, мы не можем определить точку максимума.

Cегодня мы на славу потрудились и разобрали множество важных вопросов:

• что такое функция, какой она бывает;

• что такое наименьшее и наибольшее значение функции;

• как определить и на отрезке;

• как находить наименьшее и наибольшее значение функции на интервале;

• что такое предел и производная.

Вот и ещё одна тема по математике стала понятнее! А если всё же остались вопросы, спешим ещё раз пригласить вас на уроки математики в Skysmart — мы постараемся ответить на них, закрепить материал и попрактиковаться в решении задач. Обещаем, будет увлекательно и безумно интересно!

Наименьшее и наибольшее значения функции на отрезке

• Как найти наименьшее и наибольшее значения функции на отрезке
• Ищем наименьшее и наибольшее значения функции вместе
• Найти наименьшее и наибольшее значения функции самостоятельно, а затем посмотреть решение
• Продолжаем искать наименьшее и наибольшее значения функции вместе

На рисунках ниже показано, где функция может достигать наименьшего и наибольшего значения. На левом рисунке наименьшее и наибольшее значения зафиксированы в точках локального минимума и максимума функции. На правом рисунке — на концах отрезка.

Если функция y = f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке наименьшего и наибольшего значений. Это, как уже говорилось, может произойти либо в точках экстремума, либо на концах отрезка. Поэтому для нахождения наименьшего и наибольшего значений функции, непрерывной на отрезке [a, b], нужно вычислить её значения во всех критических точках и на концах отрезка, а затем выбрать из них наименьшее и наибольшее. Кстати, будет полезным открыть в новом окне материал Свойства и графики элементарных функций.

Пусть, например, требуется определить наибольшее значение функции f(x) на отрезке [a, b]. Для этого следует найти все её критические точки, лежащие на [a, b].

Критической точкой называется точка, в которой функция определена, а её производная либо равна нулю, либо не существует. Затем следует вычислить значения функции в критических точках. И, наконец, следует сравнить между собой по величине значения функции в критических точках и на концах отрезка (f(a) и f(b)). Наибольшее из этих чисел и будет наибольшим значением функции на отрезке [a, b].

Аналогично решаются и задачи на нахождение наименьших значений функции.

Для нахождения критических точек нужно неплохо разбираться в производных и решении несложных алгебраических уравнений. В любом случае будет нужна таблица производных (откроется в новом окне), так как в примерах указано, какая именно табличная производная найдена.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 1. Найти наименьшее и наибольшее значения функции на отрезке [-1, 2].

Решение. Находим производную (первое и второе слагаемые — табличная производная 3, третье — табличная производная 1) данной функции . Приравняем производную нулю () и, решив уравнение, получим две критические точки: и . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на концах отрезка и в точке , так как точка не принадлежит отрезку [-1, 2]. Эти значения функции — следующие: , , . Из этого следует, что наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке , а наибольшее (тоже красное на графике), равно 9, — в критической точке .

Если функция непрерывна в некотором промежутке и этот промежуток не является отрезком (а является, например, интервалом; разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок), то среди значений функции может и не быть наименьшего и наибольшего. Так, например, функция, изображённая на рисунке ниже, непрерывна на ]-∞, +∞[ и не имеет наибольшего значения.

Однако для любого промежутка (закрытого, открытого или бесконечного) справедливо следующее свойство непрерывных функций.

Если функция непрерывна в промежутке и имеет единственный экстремум, то он является наименьшим значением в случае минимума и наибольшим — в случае максимума.

Как наименьшее значение функции, так и её наибольшее значение, могут быть найдены не только в одной точке, принадлежащей заданного интервала, а, как, например, далее — в двух.

Пример 2. Найти наименьшее и наибольшее значения функции на отрезке [-3, 3].

Решение. Находим производную (первое и второе слагаемые — табличная производная 3, третье — табличная производная 1) данной функции . Привыкаем к однообразным действиям: приравниваем производную нулю () и решение этого уравнения даёт нам три критические точки: , и . Все критические точки принадлежат отрезку [-3, 3]. Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и во всех критических точках. Эти значения следующие:

Видим, что функция достигает наименьшего значения, равного -13, в двух точках и и наибольшего значения, равного 12, также в двух точках и (то есть на концах отрезка).

Нередки случаи, когда уравнение, полученное от приравнивания производной функции нулю, не имеет действительных решений. Тогда наименьшее и наибольшее значения функции можно найти только на концах отрезка. Таков следующий пример.

Пример 3. Найти наименьшее и наибольшее значения функции на отрезке [0, 4].

Решение. Находим производную (первое слагаемое — табличная производная 2, второе — табличная производная 5) данной функции . Приравниваем производную нулю: . Видим, что это уравнение не имеет действительных корней. Поэтому наименьшее и наибольшее значения функции можем найти только на концах данного отрезка. Находим значения функции на концах отрезка:

Обе точки, следуя условию, годятся, так что функция достигает наименьшего значения, равного 0, в точке и наибольшего значения, равного 6, в точке .

Нет времени вникать в решение? Можно заказать работу!

Неплохо было бы взять и случаи, когда производная функции вычисляется не одним махом, как в предыдущих примерах. Это мы сейчас и сделаем, решив пример, где требуется найти производную частного.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 4. Найти наименьшее и наибольшее значения функции на отрезке [-1, 3].

Решение. Находим производную данной функции как производную частного по соответствующему правилу:

.

Приравниваем производную нулю, что даёт нам одну критическую точку: . Она принадлежит отрезку [-1, 3]. Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:

Сравниваем эти значения. Вывод: функция достигает наименьшего значения, равного -5/13, в точке и наибольшего значения, равного 1, в точке .

Пример 5. Найти наименьшее и наибольшее значения функции на отрезке .

Правильное решение и ответ.

Пример 6. Найти наименьшее и наибольшее значения функции на отрезке .

Правильное решение и ответ.

Пример 7. Найти наименьшее и наибольшее значения функции на отрезке .

Правильное решение и ответ.

• Страница 2 (Тренинг по нахождению критических точек функции)

Есть преподаватели, которые по теме нахождения наименьшего и наибольшего значений функции не дают студентам для решения примеры сложнее только что рассмотренных, то есть таких, в которых функция — многочлен либо дробь, числитель и знаменатель которой — многочлены. Но мы не ограничимся такими примерами, поскольку среди преподавателей бывают любители заставить студентов думать по полной (таблице производных). Поэтому в ход пойдут логарифм и тригонометрическая функция.

Пример 8. Найти наименьшее и наибольшее значения функции на отрезке [1, e].

Решение. Находим производную данной функции как производную произведения:

Приравниваем производную нулю, что даёт одну критическую точку: . Она принадлежит отрезку [1, e]. Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:

Результат всех действий: функция достигает наименьшего значения, равного 0, в точке и в точке и наибольшего значения, равного e², в точке .

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 9. Найти наименьшее и наибольшее значения функции на отрезке .

Решение. Находим производную (первое слагаемое — табличная производная 2, второе — табличная производная 7) данной функции:

Приравниваем производную нулю:

Единственная критическая точка принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:

Вывод: функция достигает наименьшего значения, равного , в точке и наибольшего значения, равного , в точке .

В прикладных экстремальных задачах нахождение наименьшего (наибольшего) значений функции, как правило, сводится к нахождению минимума (максимума). Но больший практический интерес имеют не сами минимумы или максимумы, а те значения аргумента, при которых они достигаются. При решении прикладных задач возникает дополнительная трудность — составление функций, описывающих рассматриваемое явление или процесс.

Пример 10. Резервуар ёмкостью 4 , имеющий форму параллелепипеда с квадратным основанием и открытый сверху, нужно вылудить оловом. Каковы должны быть размеры резервуара, чтобы на его покрытие ушло наименьшее количество материала?

Решение. Пусть x — сторона основания, h — высота резервуара, S — площадь его поверхности без крышки, V — его объём. Площадь поверхности резервуара выражается формулой , т.е. является функцией двух переменных . Чтобы выразить S как функцию одной переменной, воспользуемся тем, что , откуда . Подставив найденное выражение h в формулу для S:

или

.

Исследуем эту функцию на экстремум. Она определена и дифференцируема всюду в ]0, +∞[, причём

.

Приравниваем производную нулю () и находим критическую точку . Кроме того, при производная не существует, но это значение не входит в область определения и поэтому не может быть точкой экстремума. Итак, — единственная критическая точка. Проверим её на наличие экстремума, используя второй достаточный признак. Найдём вторую производную . При вторая производная больше нуля (). Значит, при функция достигает минимума . Поскольку этот минимум — единственный экстремум данной функции, он и является её наименьшим значением. Итак, сторона основания резервуара должна быть равна 2 м, а его высота .

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 11. Из пункта A, находящегося на линии железной дороги, в пункт С, отстоящий от неё на расстоянии l, должны переправляться грузы. Стоимость провоза весовой единицы на единицу расстояния по железной дороге равна , а по шоссе она равна . К какой точке М линии железной дороги следует провести шоссе, чтобы транспортировка груза из А в С была наиболее экономичной (участок АВ железной дороги предполагается прямолинейным)?

Пусть , , (см. рисунок ниже).

Тогда , , . Стоимость провоза p единиц груза по шоссе СМ составит , а по железной дороге МА она составит . Общая стоимость провоза груза по пути СМА выражается функцией

,

где .

Нужно найти наименьшее значение этой функции. Она дифференцируема при всех значениях x, причём

.

Приравняв производную нулю, получим иррациональное уравнение , решение которого даёт единственную критическую точку (так как точка не входит в область определения функции).

Взяв контрольные точки и слева и справа от критической точки, убедимся, что производная меняет знак с минуса на плюс. Следовательно, при стоимость провоза груза из А и С является наименьшей, если . Если же , т. е. , то шоссе должно пройти по прямой АС (см. рисунок ниже).

Назад

Листать

Вперёд>>>

К началу страницы

Пройти тест по теме Производная, дифференциал и их применение

Весь блок «Производная»

• Что такое производная
• Найти производную: алгоритм и примеры решений
• Производные произведения и частного функций
• Производная суммы дробей со степенями и корнями
• Производные простых тригонометрических функций
• Производная сложной функции
• Производная логарифмической функции
• Дифференциал функции
• Дифференциал сложной функции, инвариантность формы дифференциала
• Уравнение касательной и уравнение нормали к графику функции
• Правило Лопиталя
• Частные производные
• Применение производной к исследованию функций
• Экстремумы функции
• Асимптоты
• Возрастание, убывание и монотонность функции
• Выпуклость и вогнутость графика функции, точки перегиба
• Полное исследование функций и построение графиков
• Функции двух и трёх переменных
• Экстремумы функции двух переменных
• Условные экстремумы и функция Лагранжа

Вычислить наименьшее или наибольшее число в диапазоне

Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Дополнительно. .. Меньше

Допустим, вы хотите выяснить, у кого наименьший процент ошибок в производственном цикле на фабрике или у кого самая большая зарплата в вашем отделе. Существует несколько способов вычисления наименьшего или наибольшего числа в диапазоне.

Если ячейки находятся в непрерывной строке или столбце

1. Выберите ячейку ниже или справа от чисел, для которых вы хотите найти наименьшее число.

2. На вкладке Главная в группе Редактирование щелкните стрелку рядом с Автосумма , выберите Мин. (вычисляет наименьшее значение) или Макс. (вычисляет наибольшее значение), а затем нажмите клавишу ВВОД.

Если ячейки не находятся в непрерывной строке или столбце

Для выполнения этой задачи используйте функции MIN, MAX, SMALL или LARGE.

Пример

Скопируйте следующие данные на пустой лист.

1 2 3 4 5 6 7

А Данные 10 7 9 27 0 4 Формула Описание (Результат) = МИН(A2:A7) Наименьшее число в диапазоне (0) =МАКС. (A2:A7) Наибольшее число в диапазоне (27) =МАЛЕНЬКИЙ(A2:A7, 2) Второе наименьшее число в диапазоне (4) =БОЛЬШОЙ(A2:A7,3) Третье по величине число в диапазоне (9)

Нужна дополнительная помощь?

Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.

См. также

БОЛЬШОЙ

МАКС

МИН.

МАЛЕНЬКИЙ

Расчет I — Минимальные и максимальные значения

Онлайн-заметки Пола
Главная / Исчисление I / Применение производных / Минимальные и максимальные значения

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 4.3: Минимальные и максимальные значения

Многие из наших приложений в этой главе будут вращаться вокруг минимальных и максимальных значений функции. Хотя мы все можем визуализировать минимальное и максимальное значения функции, мы хотим быть немного более конкретными в нашей работе здесь. В частности, мы хотим различать два типа минимальных и максимальных значений. Следующее определение дает типы минимальных и/или максимальных значений, которые мы будем рассматривать.

Определение

1. Мы говорим, что \(f\left( x \right)\) имеет абсолютный (или глобальный) максимум в точке \(x = c\), если\(f\left( x \right) \le f\left( c \right)\) для каждого \(x\) в домене, над которым мы работаем.
2. Мы говорим, что \(f\left( x \right)\) имеет относительный (или локальный) максимум в точке \(x = c\), если \(f\left( x \right) \le f\left ( c \right)\) для каждого \(x\) в некотором открытом интервале вокруг \(x = c\).
3. Мы говорим, что \(f\left( x \right)\) имеет абсолютный (или глобальный) минимум в точке \(x = c\), если \(f\left( x \right) \ge f\left( c \right)\) для каждого \(x\) в области мы работают над.
4. Мы говорим, что \(f\left( x \right)\) имеет относительный (или локальный) минимум в точке \(x = c\), если\(f\left( x \right) \ge f\left ( c \right)\) для каждого \(x\) в некотором открытом интервале вокруг \(x = c\).

Обратите внимание: когда мы говорим «открытый интервал вокруг\(x = c\)», мы имеем в виду, что мы можем найти некоторый интервал \(\left( {a,b} \right)\), не включающий конечные точки, такие что \(а<с

Также мы будем вместе называть точки минимума и максимума функции экстремумами функции. Таким образом, относительные экстремумы будут относиться к относительным минимумам и максимумам, а абсолютные экстремумы — к абсолютным минимумам и максимумам.

Теперь давайте немного поговорим о тонкой разнице между абсолютным и относительным в приведенном выше определении.

У нас будет абсолютный максимум (или минимум) при \(x = c\) при условии, что \(f\left( c \right)\) является наибольшим (или наименьшим) значением, которое функция когда-либо принимала в области над которым мы работаем. Кроме того, когда мы говорим «область, над которой мы работаем», это просто означает диапазон \(x\), который мы выбрали для работы с данной проблемой. Могут быть и другие значения \(x\), которые мы действительно можем подставить в функцию, но по какой-то причине исключили их.

Относительный максимум или минимум немного отличаются. Все, что требуется для того, чтобы точка была относительным максимумом или минимумом, — это чтобы эта точка была максимумом или минимумом в некотором интервале \(x\) вокруг \(x = c\). В каком-то другом месте могут быть большие или меньшие значения функции, но относительно \(x = c\) или локально по отношению к \(x = c\), \(f\left(c \right)\) равно больше или меньше, чем все другие значения функции, которые находятся рядом с ним.

Также обратите внимание, что для того, чтобы точка была относительным экстремумом, мы должны иметь возможность смотреть на значения функции по обе стороны от \(x = c\), чтобы увидеть, действительно ли она является максимумом или минимумом в этой точке. Это означает, что относительные экстремумы не возникают в конечных точках области. Они могут возникать только внутри домена.

По предыдущему пункту ведутся споры. Некоторые люди считают, что относительные экстремумы могут возникать на конечных точках домена. Однако в этом классе мы будем использовать определение, в котором говорится, что они не могут встречаться в конечных точках домена. Это будет обсуждаться более подробно в конце раздела, как только мы позаботимся о соответствующем факте.

Обычно легче понять определения, взглянув на график.

Для функции, показанной на этом графике, мы имеем относительные максимумы в точках \(x = b\) и \(x = d\). Обе эти точки являются относительными максимумами, поскольку они находятся внутри показанной области и являются самой большой точкой на графике в некотором интервале вокруг точки. Мы также имеем относительный минимум в \(x = c\), так как эта точка находится внутри области и является самой нижней точкой на графике в интервале вокруг нее. Крайняя правая конечная точка \(x = e\) не будет относительным минимумом, поскольку это конечная точка.

Функция будет иметь абсолютный максимум в точке \(x = d\) и абсолютный минимум в точке \(x = a\). Эти две точки являются наибольшей и наименьшей величиной, которой когда-либо будет функция. Мы также можем заметить, что абсолютные экстремумы функции будут возникать либо на концах области, либо на относительных экстремумах. Мы будем использовать эту идею в следующих разделах, так что она важнее, чем может показаться в настоящее время.

Давайте быстро рассмотрим несколько примеров, чтобы убедиться, что у нас есть определения абсолютных экстремумов и относительных экстремумов. 92}\hspace{0.25in}{\mbox{on}}\hspace{0.25in}\left[ { — 1,2} \right]\]

Показать решение

Так как эту функцию достаточно легко изобразить в виде графика, давайте сделаем это. Однако нам нужен только график на интервале \(\left[ { — 1,2} \right]\). Вот график:

Обратите внимание, что мы использовали точки в конце графика, чтобы напомнить нам, что график заканчивается в этих точках.

Теперь мы можем определить экстремумы на графике. Похоже, у нас есть относительный и абсолютный минимум нуля при \(x = 0\) и абсолютный максимум четыре при \(x = 2\). Обратите внимание, что \(x = — 1\) не является относительным максимумом, поскольку он находится в конечной точке интервала. 92}\hspace{0.25in}{\mbox{on}}\hspace{0.25in}\left[ { — 2,2} \right]\]

Показать решение

Вот график для этой функции.

В этом случае у нас все еще есть относительный и абсолютный минимум нуля в точке \(x = 0\). У нас также все еще есть абсолютный максимум четыре. Однако, в отличие от первого примера, это произойдет в двух точках: \(x = — 2\) и \(x = 2\).

Опять же, функция не имеет относительных максимумов.

Как показано в этом примере, может быть только одно абсолютное максимальное или абсолютное минимальное значение, но они могут встречаться более чем в одном месте домена. 92}\]

Показать решение

В этом случае мы не указали домен, поэтому предполагается, что мы возьмем максимально возможный домен. Для этой функции это означает все действительные числа. Вот график.

В этом случае график не перестает расти ни с одной стороны, поэтому для этой функции нет никаких максимумов. Независимо от того, какую точку мы выберем на графике, с обеих сторон будут точки как больше, так и меньше, поэтому у нас не может быть никаких максимумов (любого рода, относительных или абсолютных) на графике.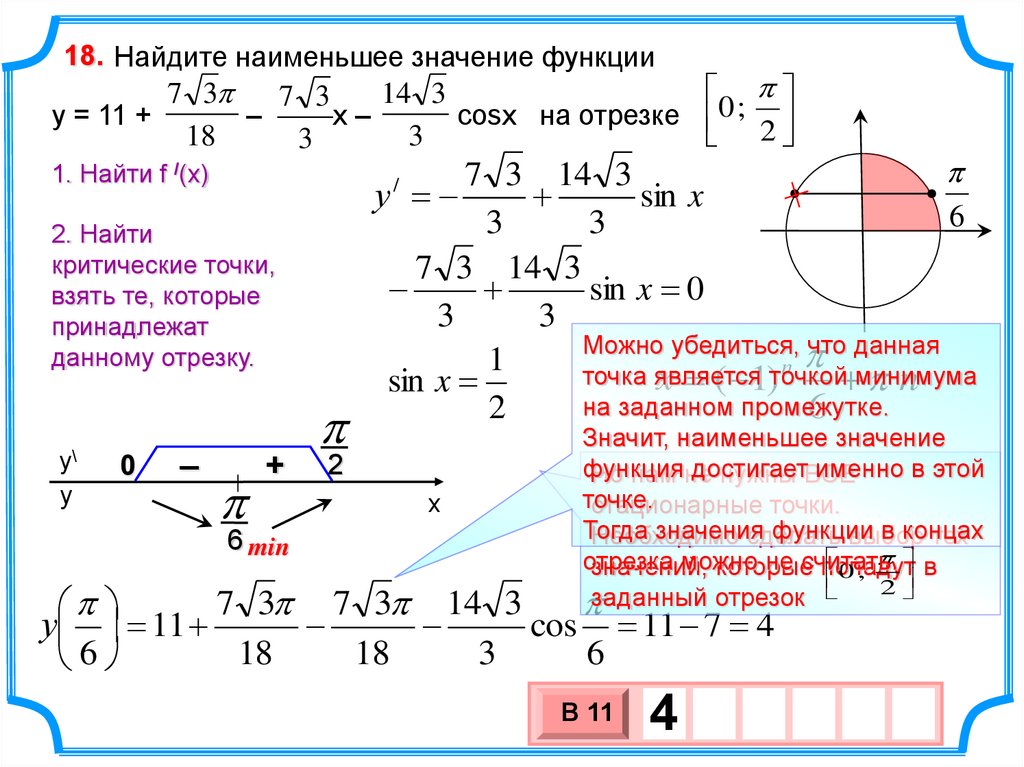 3}\]

Показать решение

Опять же, на этот раз мы не ограничиваем домен, поэтому вот график.

В этом случае функция не имеет ни относительных, ни абсолютных экстремумов.

Как мы видели в предыдущем примере, функции не обязательно должны иметь какие-либо экстремумы, относительные или абсолютные.

Пример 6 Определите абсолютный и относительный экстремумы для следующей функции. \[f\влево( x \вправо) = \cos \влево( x \вправо)\]

Показать решение

Мы не ограничивали домен для этой функции. Вот график.

Косинус имеет экстремумы (относительные и абсолютные), которые встречаются во многих точках. Косинус имеет как относительный, так и абсолютный максимум 1 на

\[x = \ldots — 4\pi ,\, — 2\pi ,\,\,0,\,\,2\pi ,\,\,4\pi , \ldots \]

Косинус также имеет как относительный, так и абсолютный минимум -1 в точке

\[x = \ldots — 3\pi ,\, — \pi ,\,\,\pi ,\,\,3\pi , \ldots \]

Как показывает этот пример, граф может иметь экстремумы в большом количестве (в данном случае бесконечном) точек.

Теперь мы рассмотрели довольно много примеров и можем использовать эти примеры, чтобы увидеть хороший факт об абсолютных экстремумах. Во-первых, давайте заметим, что все приведенные выше функции были непрерывными функциями. Далее обратите внимание, что каждый раз, когда мы ограничивали домен закрытым интервалом (, т.е. , интервал содержит его конечные точки), мы получали абсолютные максимумы и абсолютные минимумы. Наконец, только в одном из трех примеров, где мы не ограничивали домен, мы получили и абсолютный максимум, и абсолютный минимум.

Эти наблюдения приводят нас к следующей теореме.

Теорема об экстремальном значении

Предположим, что \(f\left( x \right)\) непрерывно на интервале \(\left[ {a,b} \right]\), тогда есть два числа \(a \ le c,d \le b\) так, что \(f\left( c \right)\) является абсолютным максимумом функции и \(f\left( d \right)\) является абсолютным минимумом функции .

Итак, если у нас есть непрерывная функция на интервале \(\left[ {a,b} \right]\), то мы гарантированно имеем как абсолютный максимум, так и абсолютный минимум функции где-то на интервале. 2}}}\hspace{0,25 дюйма}{\mbox{on}}\hspace{0,25in}\left[ {\frac {1}{2},1} \справа]\]

функция теперь будет иметь оба абсолютных экстремума. Мы можем столкнуться с проблемами только в том случае, если интервал содержит точку разрыва. Если нет, то теорема верна.

Следует также отметить, что только потому, что функция не является непрерывной в точке, это не означает, что у нее не будет обоих абсолютных экстремумов на интервале, содержащем эту точку. Ниже приведен график функции, которая не является непрерывной в точке заданного интервала, но имеет оба абсолютных экстремума.

Этот график не является непрерывным в точке \(x = c\), но имеет как абсолютный максимум (\(x = b\)) так и абсолютный минимум (\(x = c\)). Также отметим, что в данном случае один из абсолютных экстремумов пришелся на точку разрыва, но это не обязательно. Абсолютный минимум легко мог быть в другой конечной точке или в какой-то другой точке внутри области. Дело в том, что этот график не является непрерывным и все же имеет оба абсолютных экстремума

. Суть всего этого в том, что мы должны быть осторожны, чтобы использовать теорему об экстремальном значении только тогда, когда выполняются условия теоремы, и не истолковывать неправильно результат, если условия не соблюдены.

Чтобы использовать теорему об экстремальном значении, у нас должен быть интервал, включающий конечные точки, часто называемый закрытым интервалом, и функция должна быть непрерывной на этом интервале. Если у нас нет замкнутого интервала и/или функция не является непрерывной на интервале, то функция может иметь или не иметь абсолютных экстремумов.

Нам нужно обсудить одну последнюю тему в этом разделе, прежде чем перейти к первому основному применению производной, которое мы собираемся рассмотреть в этой главе.

Теорема Ферма

Если \(f\left( x \right)\) имеет относительный экстремум в точке \(x = c\) и \(f’\left( c \right)\) существует, то \(x = c\) является критической точкой \(f\left( x \right)\). На самом деле это будет критическая точка такая, что \(f’\left( c \right) = 0\).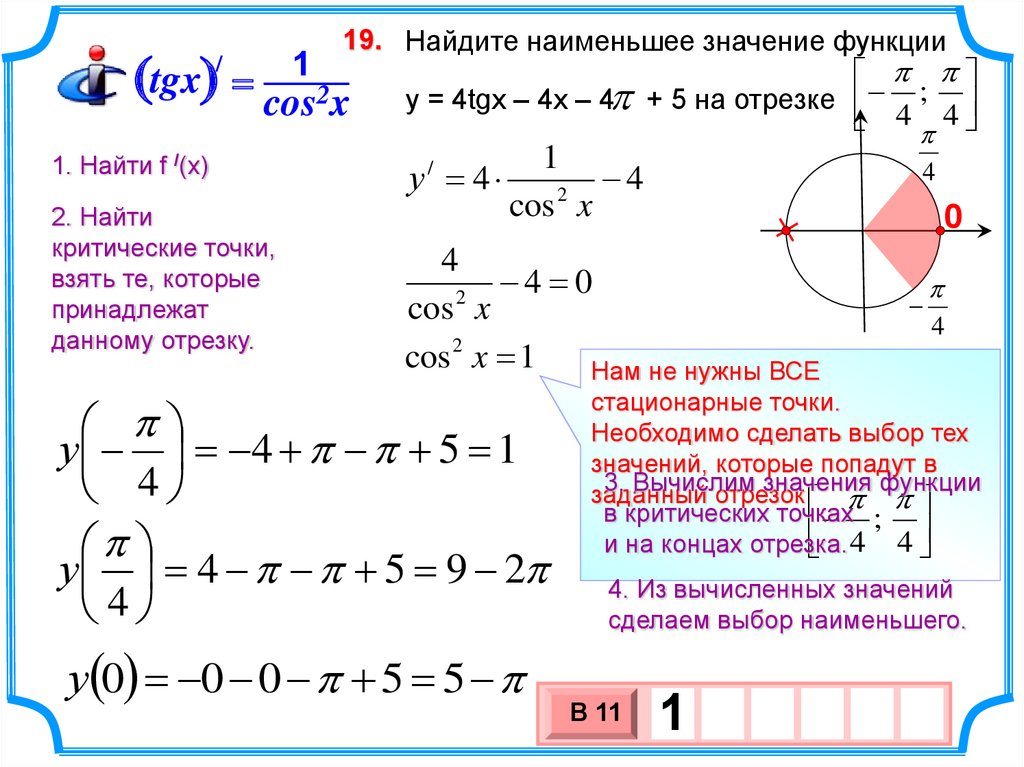

Доказательство этой теоремы см. в разделе «Доказательства производных приложений» главы «Дополнительно».

Также обратите внимание, что мы можем сказать, что \(f’\left( c \right) = 0\), потому что мы также предполагаем, что \(f’\left( c \right)\) существует. 92}\). Мы видели, что эта функция имеет относительный минимум при \(x = 0\) в нескольких более ранних примерах. Значит, по теореме Ферма \(x = 0\) должна быть критической точкой. Производная функции:

\[f’\влево( х \вправо) = 2x\]

Действительно, \(x = 0\) является критической точкой.

Не злоупотребляйте этой теоремой. Это не говорит о том, что критическая точка будет относительным экстремумом. Чтобы убедиться в этом, рассмотрим следующий случай.

92}\]

Ясно, что \(x = 0\) является критической точкой. Однако в более раннем примере мы видели, что эта функция не имеет никаких относительных экстремумов. Таким образом, критические точки не обязательно должны быть относительными экстремумами.

Также обратите внимание, что эта теорема ничего не говорит об абсолютных экстремумах. Абсолютный экстремум может быть или не быть критической точкой.

Прежде чем мы покинем этот раздел, нам нужно обсудить пару вопросов.

Во-первых, теорема Ферма работает только для критических точек, в которых \(f’\left( c \right) = 0\). Это, однако, не означает, что относительные экстремумы не будут возникать в критических точках, где производная не существует. Чтобы увидеть это, рассмотрим \(f\left( x \right) = \left| x \right|\). Очевидно, что эта функция имеет относительный минимум при \(x = 0\), но в предыдущем разделе мы показали на примере, что \(f’\left( 0 \right)\) не существует.

Все это означает, что если мы хотим найти относительные экстремумы, все, что нам действительно нужно сделать, это посмотреть на критические точки, поскольку это места, где могут существовать относительные экстремумы.

Наконец, вспомним, что в начале раздела мы заявили, что относительных экстремумов не будет в конечных точках рассматриваемого нами интервала.