Преобразование рациональных выражений: виды преобразований, примеры

Статья рассказывает о преобразовании рациональных выражений. Рассмотрим виды рациональных выражений, их преобразования, группировки, вынесения за скобки общего множителя. Научимся представлять дробные рациональные выражения в виде рациональных дробей.

Определение и примеры рациональных выражений

Определение 1

Выражения, которые составлены из чисел, переменных, скобок, степеней с действиями сложения, вычитания, умножения, деления с наличием черты дроби, называют рациональными выражениями.

Для примера имеем, что 5, 23·x-5, -3·a·b3-1c2+4a2+b21+a:(1-b), (x+1)·(y-2)x5-5·x·y·2-111·x3.

То есть это такие выражения, которые не имеют деления на выражения с переменными. Изучение рациональных выражений начинается с 8 класса, где их называют дробными рациональными выражениями. Особое внимание уделяют дробям в числителе, которые преобразовывают  с помощью правил преобразования.

Это позволяет переходить к преобразованию рациональных дробей произвольного вида. Такое выражение может быть рассмотрено как выражение с наличием рациональных дробей и целых выражений со знаками действий.

Основные виды преобразований рациональных выражений

Рациональные выражения используются для того, чтобы выполнять тождественные преобразования, группировки, приведение подобных, выполнение других действий с числами. Цель таких выражений – это упрощение.

Пример 1

Преобразовать рациональное выражение 3·xx·y-1-2·xx·y-1.

Решение

Видно, что такое рациональное выражение – это разность 3·xx·y-1 и 2·xx·y-1. Замечаем, что знаменатель у них идентичный. Это значит, что приведение подобных слагаемых примет вид

3·xx·y-1-2·xx·y-1=xx·y-1·3-2=xx·y-1

Ответ: 3·xx·y-1-2·xx·y-1=xx·y-1.

Пример 2

Выполнить преобразование 2·x·y4·(-4)·x2:(3·x-x).

Решение

Первоначально выполняем действия в скобках 3·x−x=2·x. Данное выражение представляем в виде 2·x·y4·(-4)·x2:(3·x-x)=2·x·y4·(-4)·x2:2·x. Мы приходим к выражению, которое содержит действия с одной ступенью, то есть имеет сложение и вычитание.

Избавляемя от скобок при помощи применения свойства деления. Тогда получаем, что 2·x·y4·(-4)·x2:2·x=2·x·y4·(-4)·x2:2:x.

Группируем числовые множители с переменной x, после этого можно выполнять действия со степенями. Получаем, что

2·x·y4·(-4)·x2:2:x=(2·(-4):2)·(x·x2:x)·y4=-4·x2·y4

Ответ: 2·x·y4·(-4)·x2:(3·x-x)=-4·x2·y4.

Пример 3

Преобразовать выражение вида x·(x+3)-(3·x+1)12·x·4+2.

Решение

Для начала преобразовываем числитель и знаменатель. Тогда получаем выражение вида (x·(x+3)-(3·x+1)):12·x·4+2, причем действия в скобках делают в первую очередь. В числителе выполняются действия и группируются множители. После чего получаем выражение вида x·(x+3)-(3·x+1)12·x·4+2=x2+3·x-3·x-112·4·x+2=x2-12·x+2.

Преобразуем в числителе формулу разности квадратов, тогда получаем, что

x2-12·x+2=(x-1)·(x+1)2·(x+1)=x-12

Ответ:  x·(x+3)-(3·x+1)12·x·4+2=x-12.

Представление в виде рациональной дроби

Алгебраическая дробь чаще всего подвергается упрощению при решении. Каждое рациональное приводится к этому разными способами. Необходимо выполнить все необходимые действия с многочленами для того, чтобы рациональное выражение  в итоге смогло дать рациональную дробь.

Пример 4

Представить в виде рациональной дроби a+5a·(a-3)-a2-25a+3·1a2+5·a.

Решение

Данное выражение можно представить в виде a2-25a+3·1a2+5·a. Умножение выполняется в первую очередь по правилам.

Следует начать с умножения, тогда получим, что

a2-25a+3·1a2+5·a=a-5·(a+5)a+3·1a·(a+5)=a-5·(a+5)·1(a+3)·a·(a+5)=a-5(a+3)·a

Производим представление полученного результата с исходное. Получим, что

a+5a·(a-3)-a2-25a+3·1a2+5·a=a+5a·a-3-a-5a+3·a

Теперь выполняем вычитание:

a+5a·a-3-a-5a+3·a=a+5·a+3a·(a-3)·(a+3)-(a-5)·(a-3)(a+3)·a·(a-3)==a+5·a+3-(a-5)·(a-3)a·(a-3)·(a+3)=a2+3·a+5·a+15-(a2-3·a-5·a+15)a·(a-3)·(a+3)==16·aa·(a-3)·(a+3)=16a-3·(a+3)=16a2-9

После чего очевидно, что исходное выражение примет вид 16a2-9.

Ответ: a+5a·(a-3)-a2-25a+3·1a2+5·a=16a2-9.

Пример 5

Представить xx+1+12·x-11+x  в виде рациональной дроби.

Решение

Заданное выражение записывается как дробь, в числителе которой имеется xx+1+1, а  в знаменателе 2·x-11+x. Необходимо произвести преобразования xx+1+1. Для этого нужно выполнить сложение дроби и числа. Получаем, что xx+1+1=xx+1+11=xx+1+1·(x+1)1·(x+1)=xx+1+x+1x+1=x+x+1x+1=2·x+1x+1

Следует, что xx+1+12·x-11+x=2·x+1x+12·x-11+x

Получившаяся дробь может быть записана как 2·x+1x+1:2·x-11+x.

После деления придем к  рациональной дроби вида

2·x+1x+1:2·x-11+x=2·x+1x+1·1+x2·x-1=2·x+1·(1+x)(x+1)·(2·x-1)=2·x+12·x-1

Можно решить это иначе.

Вместо деления на 2·x-11+x производим умножение на обратную ей 1+x2·x-1. Применим распределительное свойство и получаем, что

xx+1+12·x-11+x=xx+1+1:2·x-11+x=xx+1+1·1+x2·x-1==xx+1·1+x2·x-1+1·1+x2·x-1=x·1+x(x+1)·2·x-1+1+x2·x-1==x2·x-1+1+x2·x-1=x+1+x2·x-1=2·x+12·x-1

Ответ: xx+1+12·x-11+x=2·x+12·x-1.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Калькулятор рациональных уравнений



Калькулятор рациональных уравнений

Наш калькулятор поможет вам решить рациональное уравнение или неравенство. Искусственный интеллект, который лежит в основе калькулятора, даст ответ с подробным решением и пояснениями.

Калькулятор полезен старшеклассникам при подготовке к контрольным работам и экзаменам, для проверки знаний перед ЕГЭ, родителям школьников с целью контроля решения многих задач по математике и алгебре.

Наш искусственный интеллект решает сложные математические задания за секунды

Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!

Пример:

Пример:

Пример:

Переменные: Параметры:

Рациональные уравнения

В рациональных уравнениях обе части уравнения представляют собой рациональные выражения вида: s(x) = 0 или расширено: s(x) = b(x), где s(x), b(x) – рациональные выражения.

Рациональное выражение является алгебраическим выражением, которое состоит из рациональных чисел и переменной величины, соединенных с помощью сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем. Таким образом, это целые и дробные выражения без радикалов.

Действия с рациональными числами обладают свойствами действий с целыми числами.

К примеру, при умножении рациональных чисел есть дополнительное свойство – умножение взаимно обратных чисел. Для того чтобы умножить два рациональных числа, необходимо умножить модули этих чисел, а перед ответом поставить «плюс», если у множителей одинаковые знаки и «минус», если знаки разные.

Умножение рационального числа на ноль. Когда в рациональном уравнении хоть один множитель – ноль, то и произведение будет равняться нолю.

Умножение рациональных чисел с разными знаками. При умножении нескольких чисел с разными знаками, необходимо умножить модули каждого из этих чисел. Если количество множителей с отрицательными знаками – четное, то произведение всегда будет со знаком «плюс», если количество множителей с отрицательными знаками – нечетное, то и произведение будет со знаком «минус».

Делить на ноль в рациональных уравнениях, как и в обычных нельзя.

Чтобы решить рациональное уравнение, необходимо определить тип этого уравнения и применить некоторые математические хитрости, созданные для этого типа. Если Вы не помните этих хитростей, то можете воспользоваться калькулятором для решения рациональных уравнений, который быстро подберёт все корни данного уравнений.

Решением рационального уравнения будут являться корень – конкретное число, при постановке которого в уравнение даст верное равенство. Корней рационального уравнения может быть много и важно в решении не упустить ни один корень.

Также читайте нашу статью «Калькулятор иррациональных урвнений онлайн»

Бесплатный онлайн калькулятор

Наш бесплатный решатель позволит решить уравнение онлайн любой сложности за считанные секунды.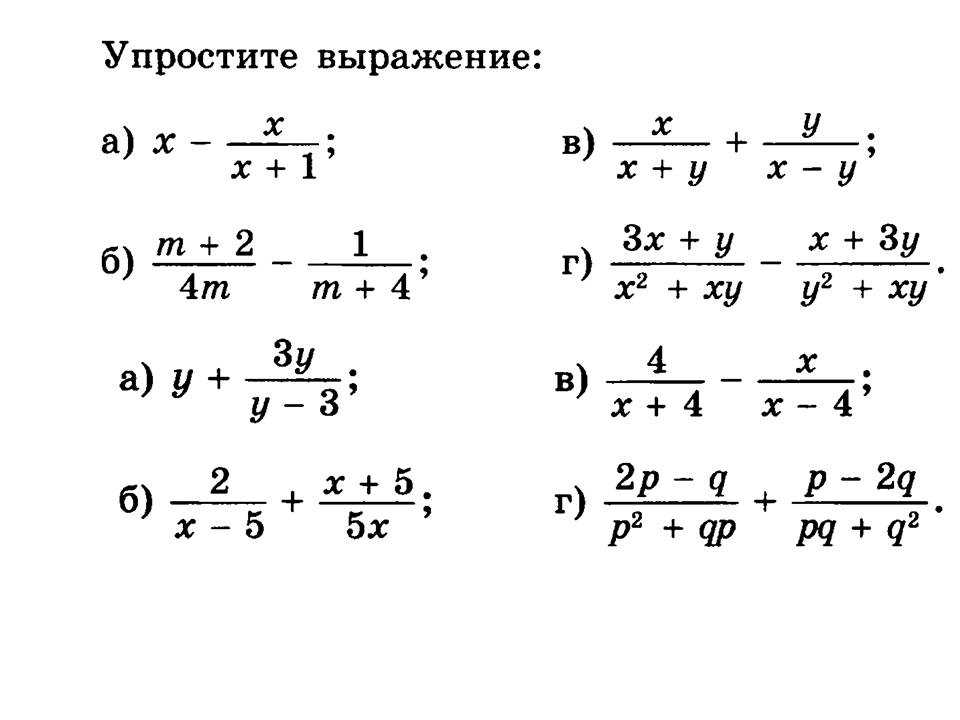 Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе ВКонтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Решение рациональных уравнений — ChiliMath

Рациональное уравнение — это тип уравнения, в котором используется хотя бы одно рациональное выражение, причудливое название дроби . Наилучший подход к решению этого типа уравнения состоит в том, чтобы исключить все знаменатели, используя идею LCD (наименьший общий знаменатель). При этом остаточное уравнение, с которым приходится иметь дело, обычно либо линейное, либо квадратичное.

В этом уроке я хочу рассмотреть десять (10) проработанных примеров разного уровня сложности. Я считаю, что большинство из нас изучает математику, рассматривая множество примеров. Вот так!

Пример 1: Решите приведенное ниже рациональное уравнение и обязательно проверьте свои ответы на наличие посторонних значений.

Было бы неплохо, если бы не было знаменателей? Ну, мы не можем просто стереть их без какого-либо действительного алгебраического шага. Подход заключается в том, чтобы найти наименьший общий знаменатель (также известный как наименьшее общее кратное) и использовать его для умножения обеих частей рационального уравнения. Это приводит к удалению знаменателей, оставляя нам обычные уравнения, которые мы уже знаем, как решать, такие как линейные и квадратные. В этом суть решения рациональных уравнений.

  • ЖК-дисплей 6x. Я умножу обе части рационального уравнения в 6 раз, чтобы исключить знаменатели. В любом случае, это наша цель – сделать нашу жизнь намного проще.
  • У вас должно получиться что-то подобное после раздачи LCD.
  • Я решил оставить переменную x справа. Поэтому удалите -5x слева, добавив обе стороны в 5x.
  • Упрощение. Теперь очевидно, как решить это одношаговое уравнение. Разделите обе части на коэффициент 5x.
  • Ага! Окончательный ответ: x = 2 после проверки исходного рационального уравнения. Это дает истинное утверждение.

Всегда сверяйте свои «решенные ответы» с исходным уравнением, чтобы исключить посторонние решения. Это критический аспект общего подхода при решении таких задач, как рациональные уравнения и радикальные уравнения.

Пример 2: Решите приведенное ниже рациональное уравнение и обязательно проверьте свои ответы на наличие посторонних значений.

Первым шагом в решении рационального уравнения всегда является поиск «серебряной пули», известной как LCD. Итак, для этой проблемы найти ЖК-дисплей просто.

Поехали.

Попробуйте представить каждый знаменатель в виде уникальных степеней простых чисел, переменных и/или членов.

Умножьте числа с наивысшими показателями для каждого уникального простого числа, переменной и/или термина, чтобы получить требуемый ЖК-дисплей.

  • ЖК-дисплей 9x. Распределите его по обеим частям уравнения, чтобы исключить знаменатели.
  • Упрощение.
  • Чтобы оставить переменные в левой части, вычтите обе части на 63.
  • Полученное уравнение представляет собой уравнение, состоящее всего из одного шага. Разделите обе части на коэффициент при x.
  • Вот оно! Проверьте значение x = — \,39 обратно в основное рациональное уравнение, и оно должно убедить вас, что оно работает.

Пример 3: Решите приведенное ниже рациональное уравнение и обязательно проверьте свои ответы на наличие посторонних значений.

Похоже, ЖК-дисплей уже отдан. У нас есть уникальный и общий член \left( {x — 3} \right) для обоих знаменателей. Число 9 имеет тривиальный знаменатель 1, поэтому я не буду его учитывать. Поэтому LCD должен быть \left( {x — 3} \right).

  • ЖК-дисплей здесь \left( {x — 3} \right). Используйте его как множитель для обеих частей рационального уравнения.
  • Надеюсь, вы получите это линейное уравнение после некоторых сокращений.

Распределить константу 9в \left( {x — 3} \right).

  • Объедините константы в левой части уравнения.
  • Упростить
  • Переместите все числа вправо, добавив 21 к обеим сторонам.
  • Упрощение
  • Не так уж плохо. Снова сделайте привычкой проверять решенный «ответ» из исходного уравнения.

Это должно работать, так что да, x = 2 — это окончательный ответ.

Пример 4: Решите приведенное ниже рациональное уравнение и обязательно проверьте свои ответы на наличие посторонних значений.

Я надеюсь, что теперь вы можете сказать, что такое ЖК-дисплей для этой проблемы при осмотре. Если нет, вы будете в порядке. Просто продолжайте повторять несколько примеров, и по мере продвижения они будут иметь больше смысла.

Попробуйте представить каждый знаменатель в виде уникальных степеней простых чисел, переменных и/или членов.

Умножьте числа с наивысшими показателями для каждого уникального простого числа, переменной и/или термина, чтобы получить требуемый ЖК-дисплей.

  • ЖК-дисплей 4\влево({x + 2}\вправо). Умножьте на него каждую часть уравнений.
  • После тщательного распределения ЖК-дисплея в рациональном уравнении, я надеюсь, что у вас есть и это линейное уравнение.

Краткое примечание : Если вы столкнулись с остатками в знаменателе после умножения, это означает, что у вас неправильный ЖК-дисплей.

Теперь распределите константы в скобках с обеих сторон.

  • Объедините константы в левой части для упрощения.
  • На этом этапе примите решение, где хранить переменную.
  • Сохранение x слева означает, что мы вычтем обе стороны на 4.
  • Упростить
  • Сложить обе стороны в 3 раза.
  • Вот и все. Проверьте свой ответ, чтобы убедиться в его достоверности.

Пример 5: Решите приведенное ниже рациональное уравнение и обязательно проверьте свои ответы на наличие посторонних значений.

Ориентируясь на знаменатели, ЖК-дисплей должен быть 6x. Почему?

Не забудьте перемножить «каждую копию» простых чисел или переменных с наивысшими степенями.

  • ЖК-дисплей 6x. Распределите по обеим частям данного рационального уравнения.
  • Так должно выглядеть после тщательной отмены аналогичных терминов.

Распределите константу в скобках.

  • Переменная x может быть объединена в левой части уравнения.
  • Поскольку слева есть только одна константа, я оставлю переменную x на противоположной стороне.
  • Итак, я вычитаю обе стороны в 5 раз. 92} + 4x — 5 = \left( {x + 5} \right)\left( {x — 1} \right). Не плохо?

    Поиск ЖК-дисплея, как и в предыдущих задачах.

    Попробуйте представить каждый знаменатель в виде уникальных степеней простых чисел, переменных и/или членов. В этом случае у нас есть термины в виде биномов.

    Умножьте числа с наивысшими показателями для каждой уникальной копии простого числа, переменной и/или термина, чтобы получить требуемый LCD.

    • Прежде чем я разложу LCD на рациональные уравнения, полностью вынесем знаменатели.

    Это помогает позже отменить условия общего пользования.

    • Умножьте каждую сторону на LCD.
    • Вау! Удивительно, как быстро был убран «беспорядок» исходной проблемы.
    • Избавьтесь от скобок по распределительному свойству.

    Вы должны решить очень простое уравнение.

    Пример 7: Решите приведенное ниже рациональное уравнение и обязательно проверьте свои ответы на наличие посторонних значений.

    Поскольку знаменатели представляют собой два уникальных бинома, вполне логично, что ЖК-дисплей — это просто их продукт.

    • ЖК-дисплей \left( {x + 5} \right)\left( {x — 5} \right). Распределите это в рациональное уравнение.
    • Получается произведение двух двучленов с обеих сторон уравнения.

    Имеет смысл использовать метод FOIL. Это звонит в колокол?

    • Я расширил обе части уравнения, используя FOIL. До этого момента у вас должна быть аналогичная установка. Теперь объедините одинаковые члены (x) в обеих частях уравнения. 92}.
    • Задача сводится к регулярному линейному уравнению из квадратного.
    • Чтобы изолировать переменную x в левой части, необходимо добавить обе части в 6x.
    • Сдвинуть все константы вправо.
    • Добавьте обе стороны на 30.
    • Наконец, разделите обе стороны на 5, и все готово.

    Пример 8: Решите приведенное ниже рациональное уравнение и обязательно проверьте свои ответы на наличие посторонних значений.

    Выглядит немного устрашающе. Но если мы будем придерживаться основ, таких как правильный поиск ЖК-дисплея и тщательное умножение его в уравнении, мы должны понять, что можем довольно легко управлять этим «зверем».

    Выражение каждого знаменателя в виде уникальных степеней членов

    Умножьте каждый уникальный член с наивысшей степенью, чтобы получить LCD

    • Вынесите знаменатели на множители.
    • Умножьте обе стороны на ЖК-дисплей, полученный выше.

    Будьте осторожны с отменой.

    • У вас должно получиться что-то подобное, если все сделано правильно.
    • Следующий шаг, распределите константы в скобках.

    С каждым шагом становится все проще!

    Я бы объединил одинаковые термины с обеих сторон также для дальнейшего упрощения.

    • Это просто многоступенчатое уравнение с переменными с обеих сторон. Легкий!
    • Чтобы оставить x слева, вычтите обе стороны на 10x.
    • Переместите все чистые числа в правую сторону.
    • Вычтите обе части на 15.
    • Простое одношаговое уравнение.
    • Разделите обе части на 5, чтобы получить окончательный ответ. Опять же, не забудьте проверить значение обратно в исходное уравнение для проверки.

    Пример 9: Решите приведенное ниже рациональное уравнение и обязательно проверьте свои ответы на наличие посторонних значений.

    Давайте найдем ЖК-дисплей для этой задачи и используем его, чтобы избавиться от всех знаменателей.

    Выразите каждый знаменатель в виде уникальных степеней термов.

    Умножьте каждый уникальный член с наивысшей степенью, чтобы определить ЖКД.

    • Полностью вынесите знаменатели на множители
    • Распределите найденный выше ЖК в данное рациональное уравнение, чтобы исключить все знаменатели.
    • Мы свели задачу к очень простому линейному уравнению. Это «магия» использования LCD.

    Умножьте константы в скобках.

    • Объединить похожие термины
    • Упростить
    • Сохраните переменную слева, вычитая x с обеих сторон.
    • Держите константы справа.
    • Добавьте обе стороны по 8, чтобы найти x. Сделанный!

    Пример 10: Решите приведенное ниже рациональное уравнение и обязательно проверьте свои ответы на наличие посторонних значений.

    Начните с определения ЖК-дисплея. Выразите каждый знаменатель в виде степени уникальных терминов. Затем перемножьте выражения с наивысших показателей для каждого уникального термина , чтобы получить требуемый ЖК-дисплей.

    Итак, мы имеем

    • Полностью вычитаем знаменатели.
    • Распределите ЖК, найденный выше, в рациональное уравнение, чтобы исключить все знаменатели.
    • Распределите константу в скобках.
    • Критический шаг : Здесь мы имеем дело с квадратным уравнением. Поэтому держите все (как переменные, так и константы) на одной стороне, заставляя противоположную сторону равняться нулю. 92} — 5x + 4 = \влево( {x — 1} \вправо)\влево( {x — 4} \вправо). Проверить это можно методом ФОЛЬГИ.
    • Используйте свойство Zero Product для нахождения x.

    Установите каждый коэффициент равным нулю, затем решите каждое простое одношаговое уравнение.

    Опять же, всегда сверяйте решенные ответы с исходными уравнениями, чтобы убедиться, что они верны.

    Вас также могут заинтересовать:

    Сложение и вычитание рациональных выражений

    Умножение рациональных выражений

    Решение рациональных неравенств

    Решение рациональных уравнений: Введение | Purplemath

    Harder ProbsGraphs

    Purplemath

    Хотя сложение и вычитание рациональных выражений может быть мучением, решение рациональных уравнений, как правило, проще, даже если в эти уравнения добавляются рациональные выражения. (Обратите внимание, я не говорю, что решение рациональных уравнений «просто», я только говорю, что это просто er .) Это потому, что, как только вы переходите от рационального выражения (то есть чего-то без знака «равно») к рациональному уравнению (то есть чему-то со знаком «равно» в середине ), вы получаете совершенно другой набор инструментов для работы. В частности, когда у вас есть этот знак «равно» в середине, у вас есть две стороны, что означает, что вы можете умножать обе эти части уравнения, и это позволяет вам избавиться от знаменателей.

    Содержимое продолжается ниже

    MathHelp.com

    Решение рациональных уравнений

    Это уравнение настолько простое, что я могу решить его, просто взглянув на него! Как?

    У меня две дроби. Эти дроби имеют одинаковый знаменатель. Эти дроби будут равны тогда, когда у них совпадают и числители, и только тогда. Так что я могу приравнять числители и получить свой ответ. Поскольку числители настолько просты, я немедленно прихожу к своему ответу:

    x = 2

    ( x − 3)/7 = (4 x + 12)/7

    В этом уравнении дроби стоят по обе стороны от знака «равно». Обе дроби имеют одинаковый знаменатель. Две дроби будут равны, когда их числители равны, поэтому я могу «приравнять» числители (то есть я могу установить их равными) и решить полученное уравнение:

    x — 3 = 4 x + 12

    -3 — 12 = 4 х — х

    -15 = 3 x

    −5 = x

    В этом уравнении есть две равные друг другу дроби (которые можно рассматривать как пропорцию). Есть три способа решить эту проблему. Я покажу каждый, а вы можете выбрать тот, который вам больше нравится.

    Метод 1: Приведение к общему знаменателю:

    Я могу привести к общему знаменателю 15:

    Теперь, когда у меня есть «(одна дробь) равна (другой дроби)», я могу приравнять числители:

    x − 1 = 6

    x = 7

    Метод 2: Умножение на общий знаменатель:

    Наименьший общий знаменатель равен 15. требовалось , если бы я складывал или вычитал эти рациональные дроби), я могу вместо этого умножить (то есть умножить обе части уравнения) на 15. Это дает мне:

    x — 1 = 2(3)

    x − 1 = 6

    x = 7

    Метод 3: перекрестное умножение:

    Термин «перекрестное умножение» не является техническим, и некоторые инструкторы его совершенно ненавидят. Но это термин, который вы услышите, и он обозначает технику, которая может быть удобной.

    Поскольку это уравнение, я могу умножать его на что угодно. В частности, чтобы избавиться от знаменателей, я могу умножить на эти знаменатели. В этом случае я бы умножил 15 из знаменателя левой части на 2 из числителя правой части; и я бы умножил 5 из знаменателя правой части на x  — 1 в числителе левой части. Другими словами, я бы сделал так:

    Этот процесс «скрещивания» знака «равно» с каждым знаменателем и умножения каждого на противоположный числитель и есть то, что подразумевается под «перекрестным умножением». Это сокращение от «умножения на общие знаменатели, когда есть только две дроби, равные самим себе, а затем упрощение того, что осталось», и может быть хорошим сокращением.

    Перемножение дает мне следующее новое (и линейное) уравнение:

    5 ( x — 1) = 15 (2)

    5 x — 5 = 30

    5 x = 35

    x = 7

    SO, на каждый из методов, методы, методы, методы, методы, методы, методы, на каждый из методов. мой ответ:

    x = 7

    Примечание: перекрестное умножение (то есть метод 3 выше) работает только , если уравнение имеет ровно одну дробь по одну сторону от знака «равно», установить равным ровно на одну дробь по другую сторону от «равно». Если в какой-либо части уравнения добавлены (или вычтены) дроби, мы должен использовать метод 1 или метод 2.

    В этом уравнении в левой части вычитаются дроби, поэтому я не могу выполнять перекрестное умножение. Кроме того, в знаменателе появился новый ряд переменных. Это означает, что мне нужно будет отслеживать значения x , которые вызовут деление на ноль. Эти значения не могут быть частью моего окончательного ответа. В этом случае знаменатели говорят мне, что мой ответ будет иметь следующее ограничение:

    x ≠ −2, 0

    Метод 1. Чтобы решить это уравнение, я могу привести все к общему знаменателю 5 x ( x  + 2), а затем сравнить числители:

    На данный момент знаменатели совпадают. Так они действительно имеют значение? Не совсем — кроме как сказать, какие значения x не могут быть из-за проблем с делением на ноль. В этот момент две части уравнения будут равны, пока равны числители. То есть все, что мне действительно нужно сделать сейчас, это решить числители:

    15 x — (5 x + 10) = x + 2

    10 x — 10 = x + 2

    9 x = 12 + 2

    9 x = 12 .