Сумма всех углов равнобедренной трапеции: Сумма двух углов равнобедренной трапеции равна 140 найти больший угол ответ дайте в градусах

Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции

Навигация по странице: Определение равнобедренной трапеции Признаки равнобедренной трапеции Основные свойства равнобедренной трапеции Стороны равнобедренной трапеции Средняя линия равнобедренной трапеции Высота равнобедренной трапеции Диагонали равнобедренной трапеции Площадь равнобедренной трапеции Окружность описанная вокруг равнобедренной трапеции

Формулы и свойства трапеции

Определение.

Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.

На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.

Рис.1

Признаки равнобедренной трапеции

Трапеция будет равнобедренной если выполняется одно из этих условий:

1. Углы при основе равны:

∠ABC = ∠BCD и ∠BAD = ∠ADC

2. Диагонали равны:

AC = BD

3. Одинаковые углы между диагоналями и основаниями:

∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

4. Сумма противоположных углов равна 180°:

∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

5. Вокруг трапеции можно описати окружность

Основные свойства равнобедренной трапеции

1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:

∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°

2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:

AB = CD = m

3. Вокруг равнобедренной трапеции можно описать окружность

4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):

h = m

5.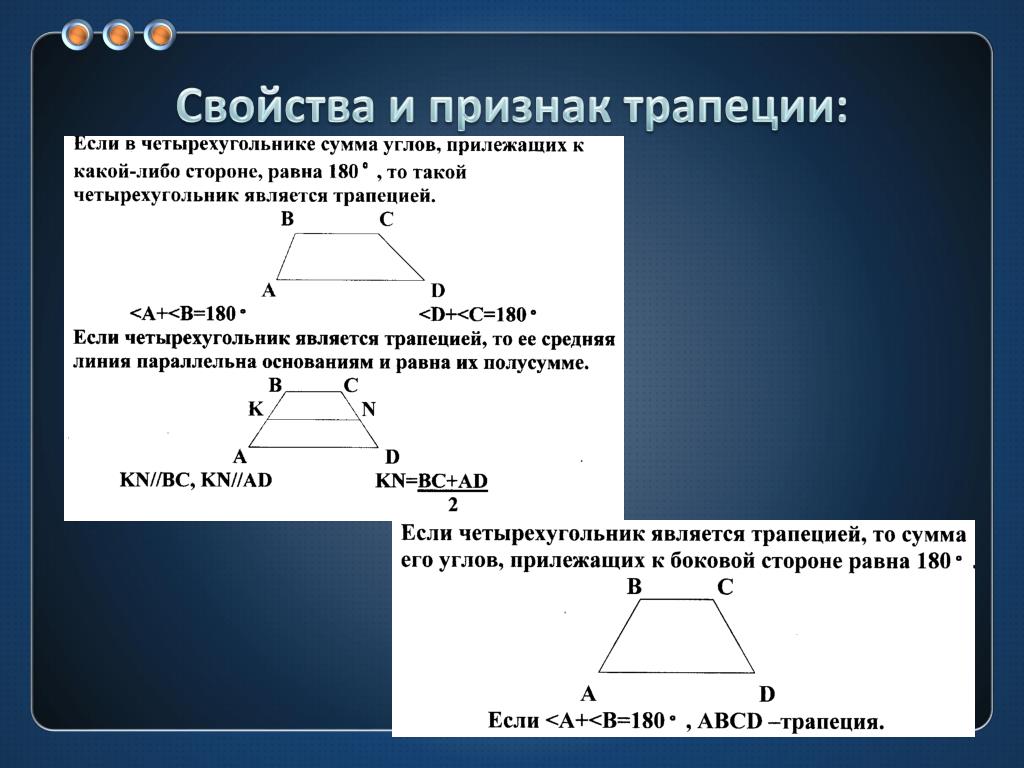 Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:

S_ABCD = h²

6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:

h² = BC · AD

7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:

AC² + BD² = AB² + CD² + 2BC · AD

8. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:

HF ┴ BC, HF ┴ AD

9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) — равен полуразности оснований:

AP =	BC + AD
	2

PD =	AD — BC
	2

10. Также смотрите свойства трапеции

Стороны равнобедренной трапеции

Формулы длин сторон равнобедренной трапеции:

1. Формулы длины сторон через другие стороны, высоту и угол:

a = b + 2h ctg α = b + 2c cos α

b = a — 2h ctg α = a — 2c cos α

c =	h	=	a — b
	sin α		2 cos α

2. Формула длины сторон трапеции через диагонали и другие стороны:

a =	d12 — c2	b =	d12 — c2	c = √d12 — ab
	b		a

3. Формулы длины основ через площадь, высоту и другую основу:

a =	2S	— b      b =	2S	— a
	h		h

4.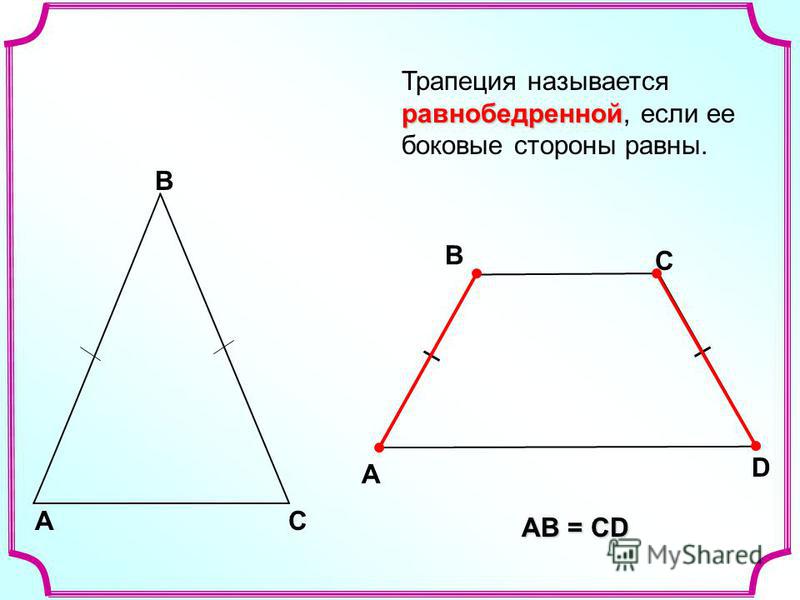 Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:

с =	S
	m sin α

5. Формулы длины боковой стороны через площадь, основания и угол при основе:

с =	2S
	(a + b) sin α

Средняя линия равнобедренной трапеции

Формулы длины средней линии равнобедренной трапеции:

1. Формула определения длины средней линии через основания, высоту и угол при основании:

m = a — h ctg α = b + h ctg α = a — √c² — h² = b + √c² — h²

2. Формула средней линии трапеции через площадь и сторону:

m =	S
	c sin α

Высота равнобедренной трапеции

Формулы определения длины высоты равнобедренной трапеции:

1.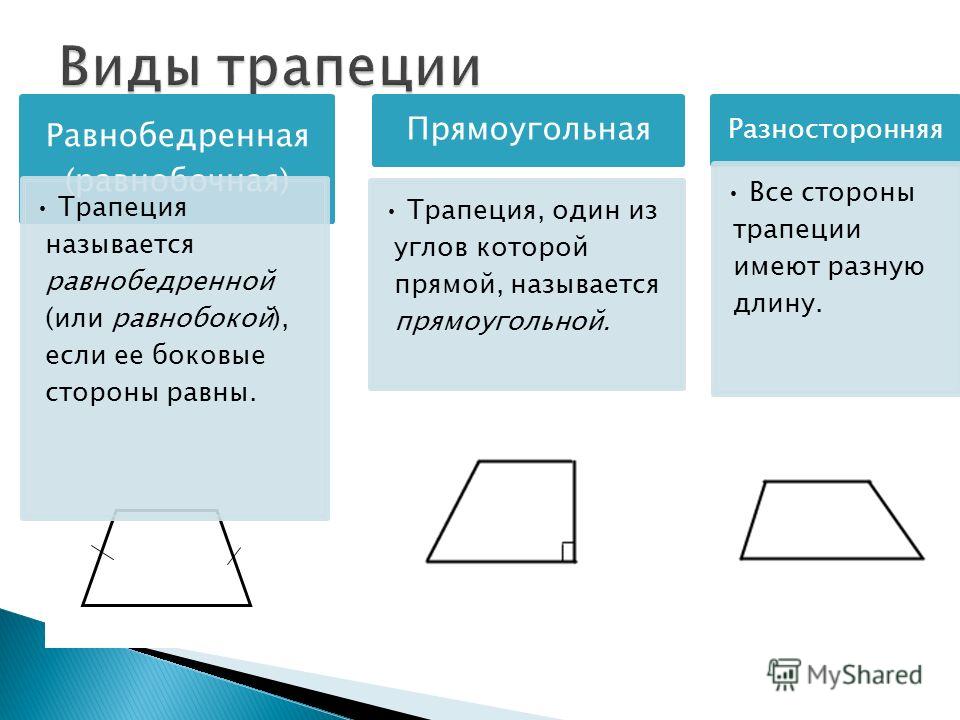 Формула высоты через стороны:

h =	1	√4c2 — (a — b)2
	2

2. Формула высоты через стороны и угол прилегающий к основе:

h =	a — b	tg β	= c sin β
	2

Диагонали равнобедренной трапеции

Диагонали равнобедренной трапеции равны:

d₁ = d₂

Формулы длины диагоналей равнобедренной трапеции:

1. Формула длины диагонали через стороны:

d₁ = √с² + ab

2. Формулы длины диагонали по теореме косинусов:

d₁ = √a² + c² — 2ac cos α

d₁ = √b² + c² — 2bc cos β

3.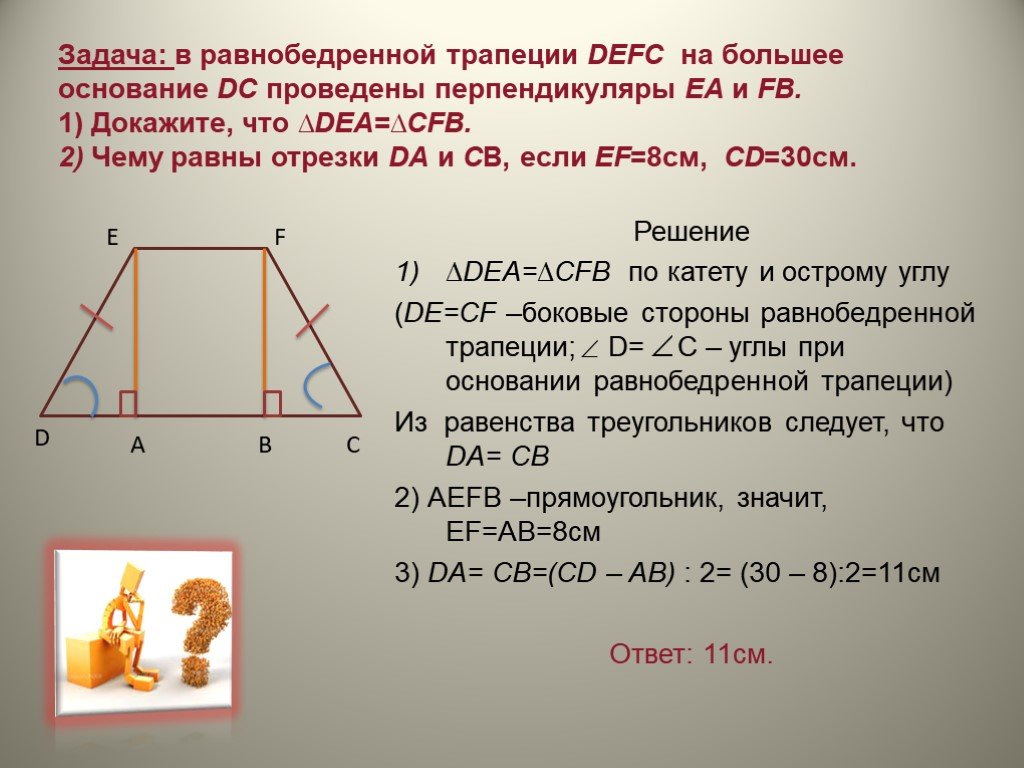 Формула длины диагонали через высоту и среднюю линию:

d₁ = √h² + m²

4. Формула длины диагонали через высоту и основания:

d1 =	1	√4h2 + (a + b)2
	2

Площадь равнобедренной трапеции

Формулы площади равнобедренной трапеции:

1. Формула площади через стороны:

S =	a + b	√4c2 — (a — b)2
	4

2. Формула площади через стороны и угол:

S = (b + c cos α) c sin α = (a — c cos α) c sin α

3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:

S =	4 r 2	=	4 r 2
	sin α		sin β

4.

Формула площади через основания и угол между основой и боковой стороной:

S =	ab	=	ab
	sin α		sin β

5. Формула площади ранобедренной трапеции в которую можно вписать окружность:

S = (a + b) · r = √ab·c = √ab·m

6. Формула площади через диагонали и угол между ними:

S =	d12	· sin γ	=	d12	· sin δ
	2			2

7. Формула площади через среднюю линию, боковую сторону и угол при основании:

S = mc sin α = mc sin β

8. Формула площади через основания и высоту:

S =	a + b	· h
	2

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d1
	4√p(p — a)(p — c)(p — d1)

где

p =	a + c + d1
	2

a — большее основание

Все таблицы и формулы

Как найти площадь в равнобедренной трапеции. Площадь трапеции: как вычислить, формула

И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.

Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции.

Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.

Трапеции обладают некоторыми интересными свойствами:

1. Средняя линия трапеции равна полусумме оснований и параллельна им.
   
2. У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
   
3. Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
   
4. Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
   
5. Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
   
6. Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
   
7. Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
   

Как найти площадь трапеции .

Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:

где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.

Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.

Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.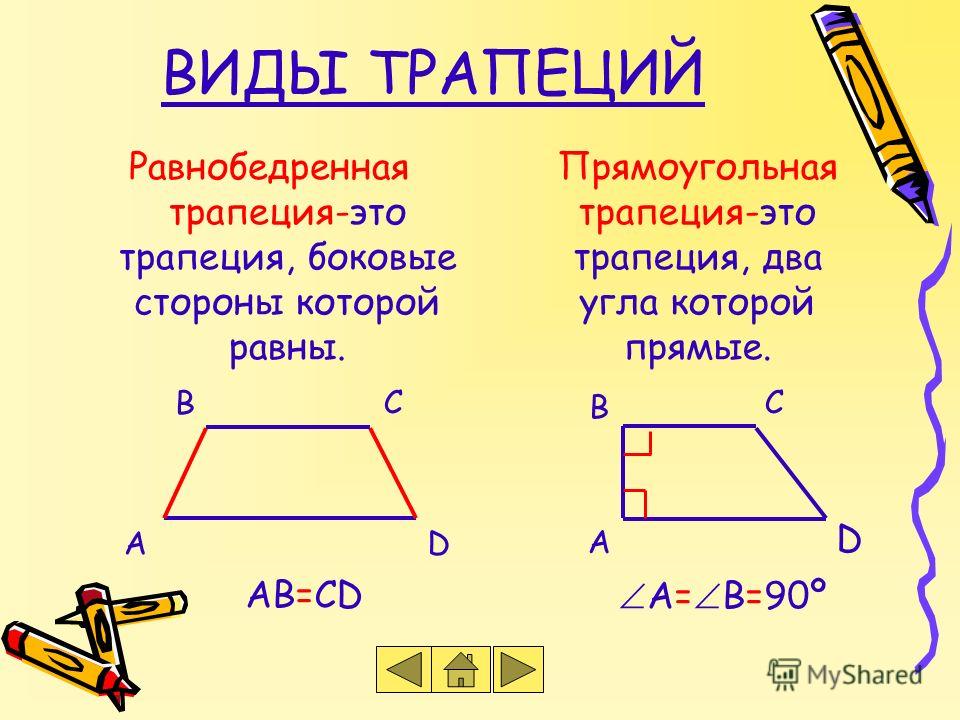

Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.

В этом случае площадь трапеции может быть найдена по формуле:

S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2

где S-площадь, a,b-основания, c,d-боковые стороны трапеции.

Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.

Многоликая трапеция… Она может быть произвольной, равнобедренной или прямоугольной.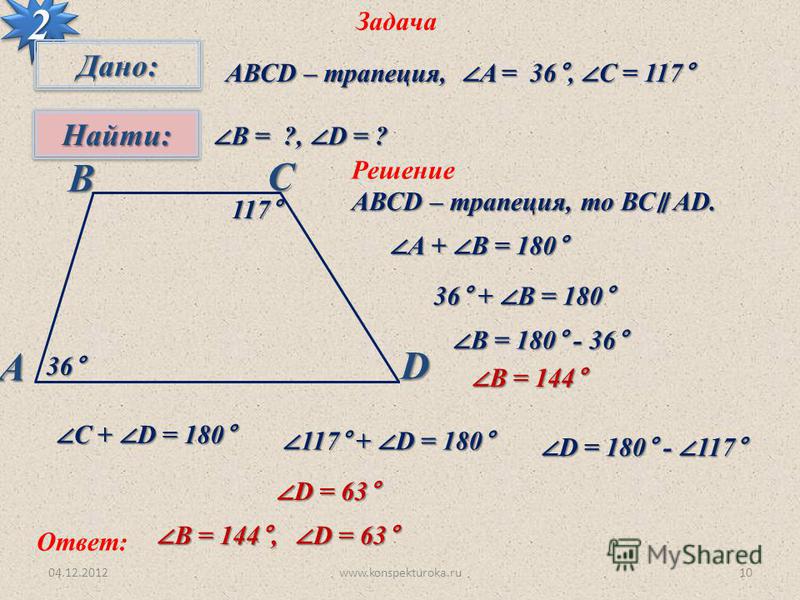 И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.

Несколько слов о трапеции и ее элементах

Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями. Большее из них — нижнее, а другое — верхнее.

Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.

Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.

Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.

Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:

• высота, то есть отрезок, перпендикулярный обоим основаниям;
• средняя линия, которая имеет своими концами середины боковых сторон.

По какой формуле вычислить площадь, если известны основания и высота?

Это выражение дается основным, потому что чаще всего можно узнать эти величины, даже когда они не даны явно. Итак, чтобы понять, как найти площадь трапеции, потребуется сложить оба основания и разделить их на два. Получившееся значение потом еще умножить на значение высоты.

Если обозначить основания буквами а 1 и а 2 , высоту — н, то формула для площади будет выглядеть так:

S = ((а 1 + а 2)/2)*н.

Формула, по которой вычисляется площадь, если даны ее высота и средняя линия

Если посмотреть внимательно на предыдущую формулу, то легко заметить, что в ней явно присутствует значение средней линии. А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:

S = l * н.

Возможность найти площадь по диагоналям

Этот способ поможет, если известен угол, образованный ими. Предположим, что диагонали обозначены буквами д 1 и д 2 , а углы между ними — α и β. Тогда формула того, как найти площадь трапеции, будет записана следующим образом:

S = ((д 1 * д 2)/2) * sin α.

В этом выражении можно легко заменить α на β. Результат не изменится.

Как узнать площадь, если известны все стороны фигуры?

Бывают и такие ситуации, когда в этой фигуре известны именно стороны. Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в 1 и в 2 , основание а 1 больше, чем а 2 . Тогда формула площади примет такой вид:

S = ((а 1 + а 2) / 2) * √ {в 1 2 — [(а 1 — а 2) 2 + в 1 2 — в 2 2) / (2 * (а 1 — а 2))] 2 }.

Способы вычисления площади равнобедренной трапеции

Первый связан с тем, что в нее можно вписать окружность. И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:

S = (4 * r 2) / sin γ.

Последняя общая формула, которая основана на знании всех сторон фигуры, существенно упростится за счет того, что боковые стороны имеют одинаковое значение:

S = ((а 1 + а 2) / 2) * √ {в 2 — [(а 1 — а 2) 2 / (2 * (а 1 — а 2))] 2 }.

Методы вычисления площади прямоугольной трапеции

Понятно, что подойдет любой из перечисленных для произвольной фигуры. Но иногда полезно знать об одной особенности такой трапеции. Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.

Часто формулы для трапеции забываются, в то время как выражения для площадей прямоугольника и треугольника помнятся. Тогда можно применить простой способ. Разделить трапецию на две фигуры, если она прямоугольная, или три. Одна точно будет прямоугольником, а вторая, или две оставшиеся, треугольниками. После вычисления площадей этих фигур останется их только сложить.

Это достаточно простой способ того, как найти площадь прямоугольной трапеции.

Как быть, если известны координаты вершин трапеции?

В этом случае потребуется воспользоваться выражением, которое позволяет определить расстояние между точками. Его можно применить три раза: для того, чтобы узнать оба основания и одну высоту. А потом просто применить первую формулу, которая описана немного выше.

Для иллюстрации такого метода можно привести такой пример. Даны вершины с координатами А(5; 7), В(8; 7), С(10; 1), Д(1; 1). Нужно узнать площадь фигуры.

До того как найти площадь трапеции, по координатам нужно вычислить длины оснований. Потребуется такая формула:

длина отрезка = √{(разность первых координат точек) 2 + (разность вторых координат точек) 2 }.

Верхнее основание обозначено АВ, значит, его длина будет равна √{(8-5) 2 + (7-7) 2 } = √9 = 3. Нижнее — СД = √ {(10-1) 2 + (1-1) 2 } = √81 = 9.

Теперь нужно провести высоту из вершины на основание. Пусть ее начало будет в точке А. Конец отрезка окажется на нижнем основании в точке с координатами (5; 1), пусть это будет точка Н. Длина отрезка АН получится равной √{(5-5) 2 + (7-1) 2 } = √36 = 6.

Осталось только подставить получавшиеся значения в формулу площади трапеции:

S = ((3 + 9) / 2) * 6 = 36.

Задача решена без единиц измерения, потому что не указан масштаб координатной сетки. Он может быть как миллиметр, так и метр.

Примеры задач

№ 1. Условие. Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.

Решение. Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).

Теперь нужно воспользоваться подходящей формулой для площади:

S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (дм 2). Задача решена.

Ответ: площадь трапеции равна 4,5 дм 2 .

№ 2. Условие. В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е — середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.

Решение. Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх. Так ЕН окажется внутри фигуры.

Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.

Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.

Таким образом, площадь трапеции равна 5 * 4 = 20 см 2 .

Ответ: S = 20 см 2 .

№ 3. Условие. Элементы равнобедренной трапеции имеют такие значения: нижнее основание — 14 см, верхнее — 4 см, острый угол — 45º. Нужно вычислить ее площадь.

Решение. Пусть меньшее основание имеет обозначение ВС. Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).

Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.

S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2).

Ответ: Искомая площадь равна 45 см 2 .

№ 4. Условие. Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.

Решение. Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т; вторую через Е и точкой пересечения с АД будет М.

Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н 1 , большей АОЕД — н 2 .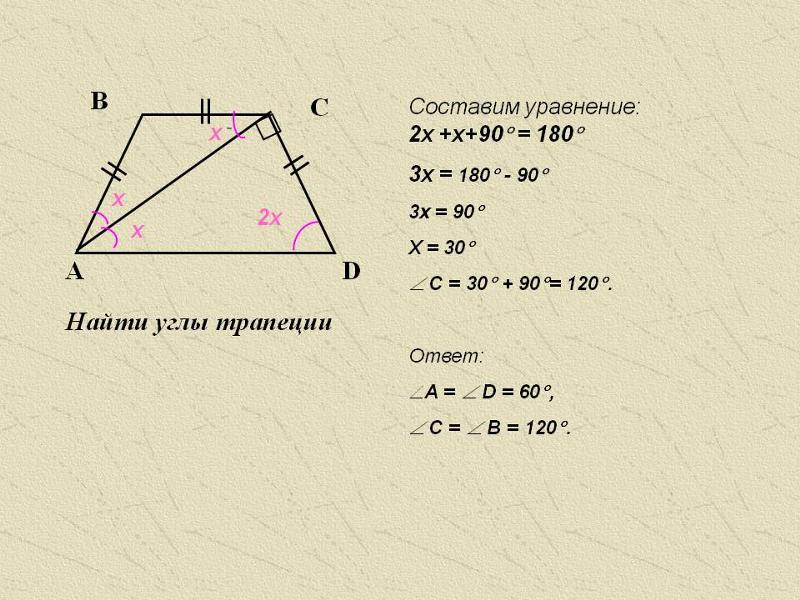

Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:

(х + а 2) * н 1 = 1/5 (х + а 1) * н 2

н 1 /н 2 = (х + а 1) / (5(х + а 2)).

Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:

н 1 /н 2 = (х — а 2) / (а 1 — х).

В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а 1) / (5(х + а 2)) равно (х — а 2) / (а 1 — х).

Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.

В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь квадратный корень.

Ответ : х = √ {(а 1 2 + 5 а 2 2) / 6}.

Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.

В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.

Что нужно знать про трапецию?

Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.

В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.

Формулы площади трапеции

Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.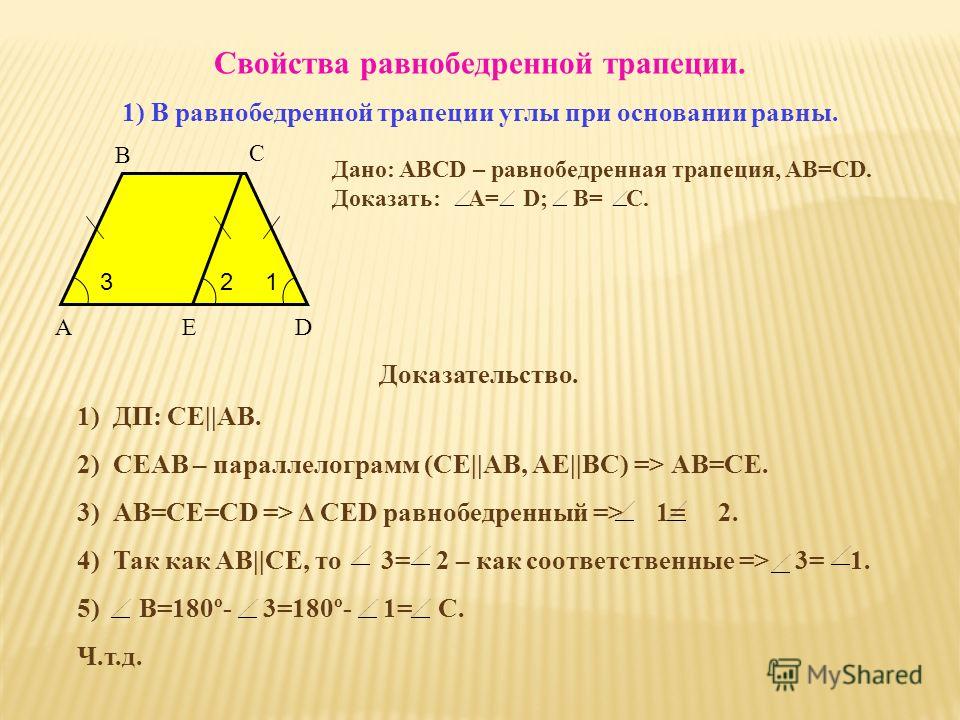

Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .

Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.

Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .

Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d.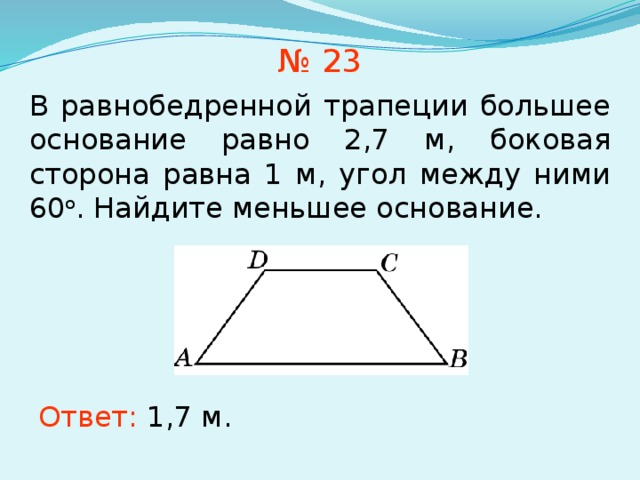 Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .

Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.

Равнобедренная трапеция

Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.

Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.

Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα . Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .

Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .

Формула площади криволинейной трапеции

Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.

Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами.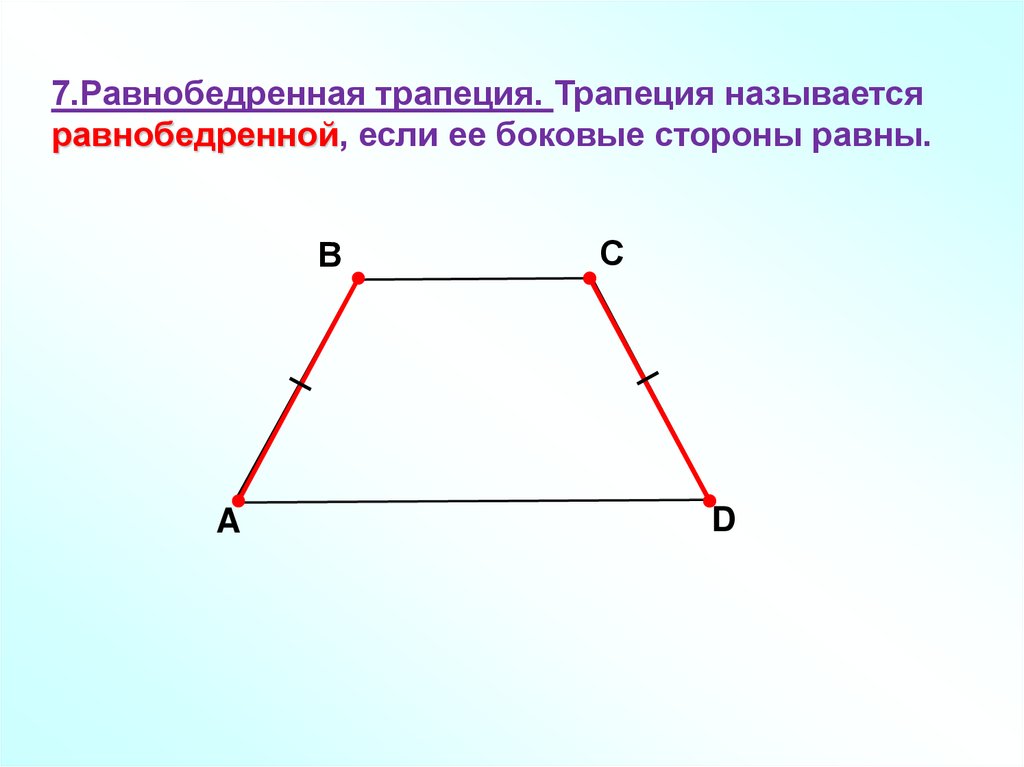 Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.

Примеры задач

Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.

Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.

Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.

Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.

Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.

Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .

Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.

Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .

Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.

Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.

Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).

Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).

Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.

Таким образом, ОЕ = х = √(5а 2 + b 2)/6.

Заключение

Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.

Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.

Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))

Теперь подробно и по порядку.

Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.

Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.

В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:

Следующее важное понятие.

Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.

Теперь давайте вникнем глубже. Почему именно так?

Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:

*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.

Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое.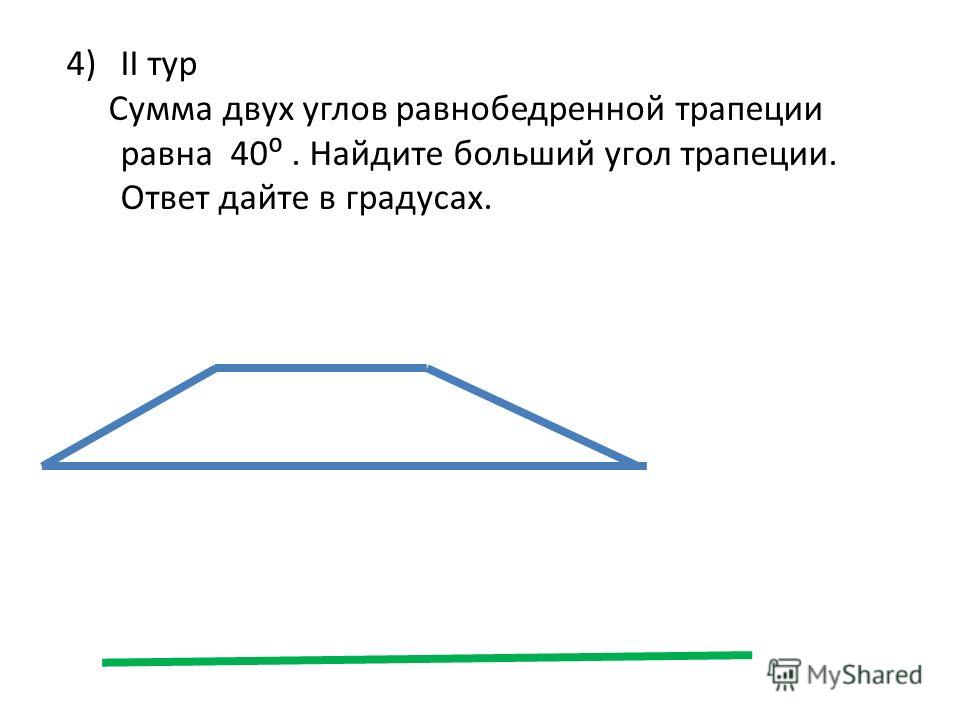 Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).

Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.

Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:

Посмотреть ещё одно объяснение

Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:

Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.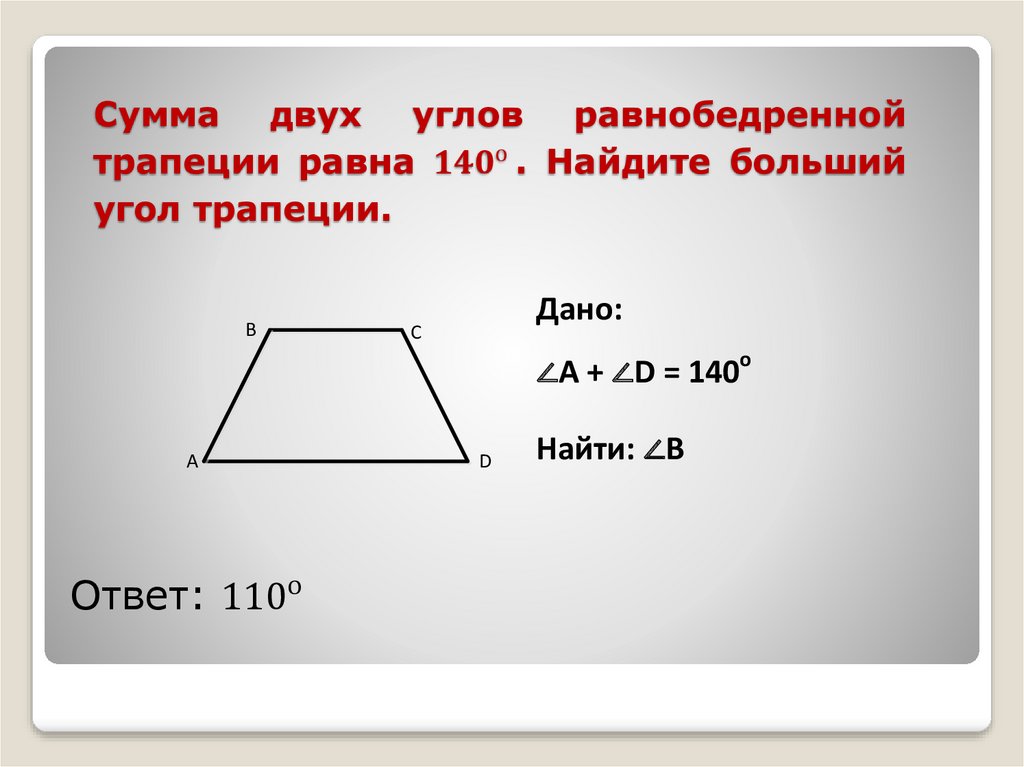

Теперь рассмотрим треугольник:

*Средняя линия данной трапеции и средняя линия треугольника совпадают.

Известно, что треугольника равна половине параллельного ей основания, то есть:

Хорошо, разобрались. Теперь о площади трапеции.

Площадь трапеции формула:

Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.

То есть, получается, что она равна произведению средней линии и высоты:

Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:

То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:

Но дело тут не в записи, конечно, а в понимании.

Скачать (посмотреть) материал статьи в формате *pdf

На этом всё. Успеха вам!

С уважением, Александр.

Равнобедренная трапеция – формула, свойства, определение, примеры

Равнобедренная трапеция – это трапеция с конгруэнтными углами при основании и конгруэнтными непараллельными сторонами. Трапеция – это четырехугольник, у которого параллельна только одна сторона. Равнобедренная трапеция обладает многими интересными свойствами, которые делают ее уникальной и помогают нам отличить ее от других четырехугольников. Давайте обсудим их подробно.

1.	Равнобедренная трапеция Определение
2.	Свойства равнобедренной трапеции
3.	Формула равнобедренной трапеции
4.	Часто задаваемые вопросы о равнобедренной трапеции

Определение равнобедренной трапеции

Равнобедренная трапеция может быть определена как трапеция, у которой непараллельные стороны и углы при основании имеют одинаковую величину.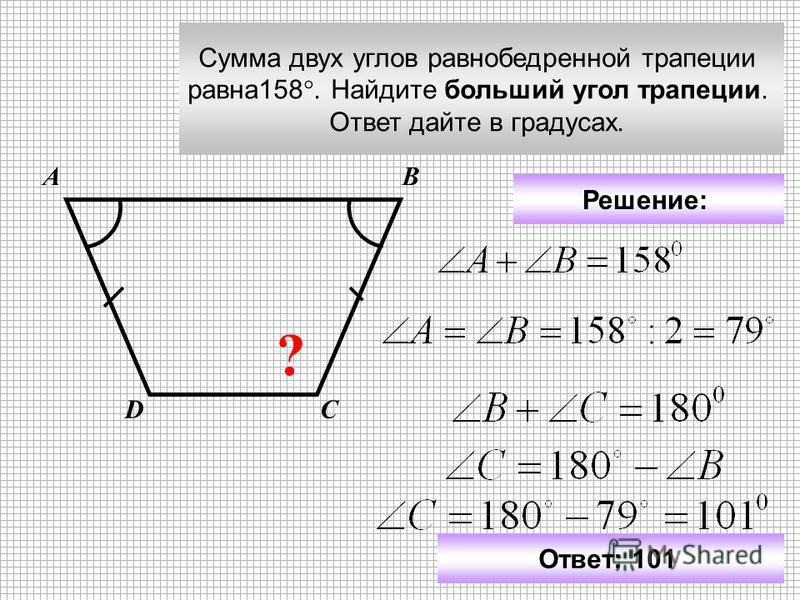 Другими словами, если две противоположные стороны (основания) трапеции параллельны, а две непараллельные стороны имеют одинаковую длину, то это равнобедренная трапеция. Посмотрите на изображение ниже: стороны c и d равны по длине, а противоположные стороны a и b (основания трапеции) параллельны друг другу.

Свойства равнобедренной трапеции

Ниже приведены свойства равнобедренной трапеции согласно рисунку, приведенному ниже.

• Имеет ось симметрии. Он не имеет вращательной симметрии и имеет одну линию симметрии, соединяющую середины параллельных сторон.
• Одна пара сторон параллельна и является базовой стороной. (AB II DC на данном изображении)
• Остальные стороны, кроме основания, непараллельны и равны по длине. (c = d на данном изображении)
• Диагонали имеют одинаковую длину. (АС = БД)
• Углы основания одинаковые. (∠D = ∠C, ∠A=∠B)
• Сумма противоположных углов равна 180° или дополнительным. (∠A + ∠C = 180° и ∠B + ∠D = 180°)
• Отрезок, соединяющий середины параллельных сторон, перпендикулярен основаниям. (PQ ⊥ DC)

Формула равнобедренной трапеции

Ниже приведены формулы для расчета площади и периметра равнобедренной трапеции.

Площадь равнобедренной трапеции

Чтобы найти площадь равнобедренной трапеции, мы должны сложить стороны основания или параллельные стороны и разделить на 2, а затем умножить результат на высоту.
Площадь равнобедренной трапеции = (сумма параллельных сторон ÷ 2) × h

Периметр равнобедренной трапеции

Чтобы найти периметр равнобедренной трапеции, мы должны сложить все стороны равнобедренной трапеции.
Периметр равнобедренной трапеции = сумма всех сторон

Похожие статьи о равнобедренной трапеции

Ознакомьтесь с интересными темами, чтобы узнать больше о равнобедренной трапеции.

• Формула трапеции
• Площадь трапеции
• Периметр трапеции Формула
• Калькулятор равнобедренных трапеций

 

Примеры на равнобедренной трапеции

1. Пример 1: Найдите высоту равнобедренной трапеции, если ее площадь равна 128 дюймов ² и длины оснований 12 дюймов и 20 дюймов.
   Решение: Данная площадь = 128 дюймов ² , основания = 12 дюймов и 20 дюймов
   мы знаем, что площадь равнобедренной трапеции = (сумма параллельных сторон ÷ 2) × высота
   следовательно, 128 = [(12 + 20) ÷ 2] × высота
   Высота = 128/16 = 8 дюймов

2. Пример 2: Найдите площадь равнобедренной трапеции, если ее основания 3 дюйма и 5 дюймов, а высота 4 дюйма.
   Решение: Площадь равнобедренной трапеции = (сумма параллельных сторон ÷ 2) × высота
   дано, основания = 3 дюйма и 5 дюймов, высота = 4 дюйма
   Площадь = [(3 + 5) ÷ 2] × 4
   Площадь = 16 дюймов ²

3. Пример 3: Найдите периметр равнобедренной трапеции, если ее основания равны 20 и 25 дюймов, а непараллельные стороны по 30 дюймов каждая.
   Решение: Периметр равнобедренной трапеции = сумма всех сторон равнобедренной трапеции
   Периметр равнобедренной трапеции = 20 + 25 + 30 + 30 = 105 дюймов

перейти к слайду перейти к слайду перейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по равнобедренной трапеции

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о равнобедренной трапеции

Что такое равнобедренная трапеция?

Равнобедренная трапеция — это тип трапеции, у которой непараллельные стороны равны друг другу. Равнобедренная трапеция — это тип четырехугольника, в котором линия симметрии делит пополам одну пару противоположных сторон. Основания равнобедренной трапеции параллельны друг другу, а стороны равны по размеру.

Каковы свойства равнобедренной трапеции?

У равнобедренной трапеции четыре стороны. Две противоположные стороны (основания) параллельны друг другу, а две другие стороны равны по длине, но не параллельны друг другу.

Если один угол при основании равнобедренной трапеции равен 30°. Найдите другой угол при основании.

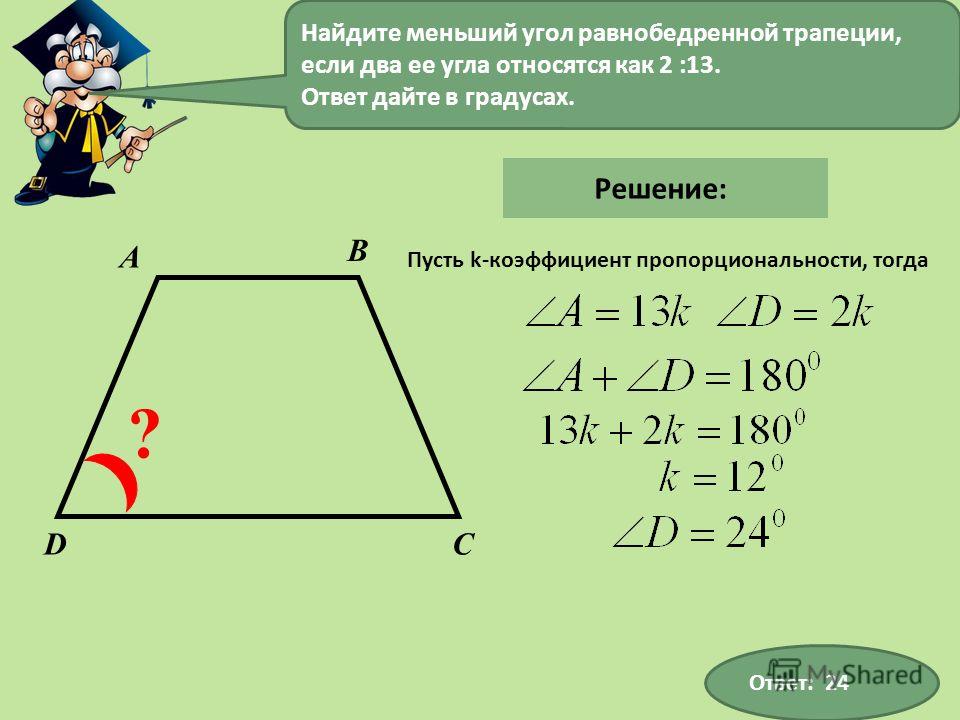
Согласно свойству равнобедренной трапеции углы при основании равны, поэтому если один угол при основании равен 30°, то и другой угол при основании будет равен 30°.

В чем разница между трапецией и равнобедренной трапецией?

В трапеции каждая сторона имеет разную длину и диагонали не равны, тогда как в равнобедренной трапеции непараллельные стороны равны, углы при основании равны, диагонали равны, а противоположные углы дополняют друг друга.

Какая формула площади равнобедренной трапеции?

Формула для расчета площади равнобедренной трапеции: Площадь = (сумма параллельных сторон ÷ 2) × высота.

Какая формула для периметра равнобедренной трапеции?

Формула для вычисления периметра равнобедренной трапеции: Периметр = сумма всех сторон равнобедренной трапеции

Скачать БЕСПЛАТНО учебные материалы

Рабочие листы по геометрии

Трапеции и их свойства

Овладейте 7 столпами школьного успеха

Улучшите свои оценки и снизьте стресс

Связанные сайты. ..0073

Средняя часть трапеции (также называемая медианой) создается путем проведения линии от середины одной стороны до середины другой стороны.

Длину миделя можно рассчитать, сложив длину двух оснований и разделив на два.

Мидель EF = AB + DC /2

Трапеция может иметь прямой угол

∠A и ∠B и ∠D и ∠C равны

∠A и ∠C и ∠B и ∠D дополняют друг друга углы и являются дополнительными. (прибавьте к 180 градусам)

∠A и ∠D и ∠B и ∠C смежные и дополнительные

• Трапеция – это четырехугольник, у которого ровно одна пара параллельных сторон.
  

• Параллельные стороны трапеции образуют основания.
  

• Сумма внутренних углов трапеции равна 360 градусов, а углы на каждой стороне трапеции являются дополнительными.
  

• Трапеция имеет четыре вершины, также называемые углами.
  

• Медиана трапеции — это линия, соединяющая середины двух сторон.
  

• Трапеция имеет одну пару параллельных сторон. Параллелограмм имеет две пары параллельных сторон.
  

• Кроме того, есть прямые трапеции и равнобедренные трапеции.
  

• Равнобедренная трапеция — это трапеция с двумя параллельными сторонами, а две другие стороны конгруэнтны.
  

• Кроме того, диагонали равнобедренного треугольника равны.
  

• Углы при основании равнобедренной трапеции равны.
  

• Прямоугольная трапеция имеет два прямых угла.
  

• В Великобритании трапеция называется трапецией
  

Стандарт Common Core. 7.G.6

Трапеция – это четырехугольник.
Трапеция имеет две параллельные стороны и две непараллельные стороны.
Внутренние углы трапеции добавляются к 360 градусам, а углы с каждой стороны являются дополнительными.
Формула площади трапеция равна   Площадь  = 1/2 (b1+b2) ч   ч = высота б = база
Формула периметра трапеция равна   Периметр = b1 +b2+s1+s2
Высота Трапеция ч= г * SinB или h =w * SinA
Диагонали длина