Правильная треугольная пирамида (правильная пирамида с треугольником в основании). Тетраэдр

В этом уроке приведены определение и свойства правильной треугольной пирамиды и ее частного случая — тетраэдра (см. ниже). Ссылки на примеры решения задач приведены в конце урока.

Определение

Правильная треугольная пирамида — это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания.


На рисунке обозначены:
ABC — Основание пирамиды
OS — Высота
KS — Апофема
OK — радиус окружности, вписанной в основание
AO — радиус окружности, описанной вокруг основания правильной треугольной пирамиды
SKO — двугранный угол между основанием и гранью пирамиды (в правильной пирамиде они равны)

Важно. В правильной треугольной пирамиде длина ребра (на рисунке AS, BS, CS ) может быть не равна длине стороны основания (на рисунке AB, AC, BC).

Если длина ребра правильной треугольной пирамиды равна длине стороны основания, то такая пирамида называется тетраэдром (см. ниже).

Свойства правильной треугольной пирамиды:
  • боковые ребра правильной пирамиды равны
  • все боковые грани правильной пирамиды являются равнобедренными треугольниками
  • в правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу
  • если центры вписанной и описанной вокруг правильной треугольной пирамиды, сферы совпадают, то сумма плоских углов при вершине пирамиды равна π (180 градусов) , а каждый из них соответственно равен π / 3  (пи делить на 3 или 60 градусов ).
  • площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
  • вершина пирамиды проецируется на основание в центр правильного равностороннего треугольника,, который является центром вписанной окружности и точкой пересечения медиан

Формулы для правильной треугольной пирамиды

Формула объема правильной треугольной пирамиды:


где

V — объем правильной пирамиды, имеющей в основании правильный (равносторонний) треугольник
h — высота пирамиды
a — длина стороны основания пирамиды
R — радиус описанной окружности
r — радиус вписанной окружности

Поскольку правильная треугольная пирамида является частным случаем правильной пирамиды, то формулы, которые верны для правильной пирамиды, верны и для правильной треугольной — см. формулы для правильной пирамиды.

Примеры решения задач:

  • Нахождение периметра правильной треугольной пирамиды 
  • Вычисление объема 
  • Нахождение площади поверхности   

    Тетраэдр

    Частным случаем правильной треугольной пирамиды является тетраэдр.

    Тетраэдр — это правильный многогранник (правильная треугольная пирамида) у которой все грани являются правильными треугольниками.

    У тетраэдра:

    • Все грани равны
    • 4 грани, 4 вершины и 6 ребер
    • Все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны

    Медиана тетраэдра — это отрезок, соединяющий вершину с точкой пересечения медиан противоположной грани (медиан равностороннего треугольника, противолежащего вершине)

    Бимедиана тетраэдра — это отрезок, соединяющий середины скрещивающихся рёбер (соединяющий середины сторон треугольника, являющегося одной из граней тетраэдра)

    Высота тетраэдра — это отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани (то есть является высотой, проведенной от любой грани, также совпадает с центром описанной окружности).

    Тетраэдр обладает следующими свойствами:

    • Все медианы и бимедианы тетраэдра пересекаются в одной точке
    • Эта точка делит медианы в отношении 3:1, считая от вершины
    • Эта точка делит бимедианы пополам

    Площадь, объем, высота, радиус вписанной и описанной окружности и другие формулы для тетраэдра

      См. пример задачи: формулы и свойства тетраэдра.


      Содержание главы:

      • Периметр основания правильной треугольной пирамиды
      • Объем правильной треугольной пирамиды
      • Площадь поверхности правильной треугольной пирамиды
      • Площадь боковой поверхности правильной треугольной пирамиды
      • Правильный тетраэдр (пирамида)
      • Пирамида и вписанный конус

      0  

       Пирамида с равнобедренным треугольником в основании | Описание курса | Периметр основания правильной треугольной пирамиды 

         

      Что такое правильная пирамида: определение, виды, свойства

      Sign in

      Password recovery

      Восстановите свой пароль

      Ваш адрес электронной почты

      MicroExcel. ru Математика Геометрия Что такое правильная пирамида: определение, виды, свойства

      В данной публикации мы рассмотрим определение, виды (треугольная, четырехугольная, шестиугольная) и основные свойства правильной пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

      • Определение правильной пирамиды
      • Виды правильной пирамиды
        • Правильная треугольная пирамида
        • Правильная четырехугольная пирамида
        • Правильная шестиугольная пирамида
      • Свойства правильной пирамиды

      Определение правильной пирамиды

      Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.

      Самые распространенные разновидности правильных пирамид: треугольная, четырехугольная и шестиугольная. Рассмотрим их подробнее.

      Виды правильной пирамиды

      Правильная треугольная пирамида

      • Основание – правильный/равносторонний треугольник ABC.
      • Боковые грани – одинаковые равнобедренные треугольники: ADC, BDC и ADB.
      • Проекция вершины D на основание – точка O, которая является точкой пересечения высот/медиан/биссектрис треугольника
        ABC        .
      • DO – высота пирамиды.
      • DL и DM – апофемы, т.е. высоты боковых граней (равнобедренных треугольников). Всего их три (по одной на каждую грань), но на рисунке выше изображено два, чтобы не перегружать его.
      • ⦟DAM = ⦟ DBL = α (углы между боковыми ребрами и основанием).
      • ⦟DLB = ⦟DMA = β (углы между боковыми гранями и плоскостью основания).
      • Для такой пирамиды верно соотношение:
        AO:OM = 2:1 или BO:OL = 2:1.

      Примечание: если у правильной треугольной пирамиды все ребра равны, она также называется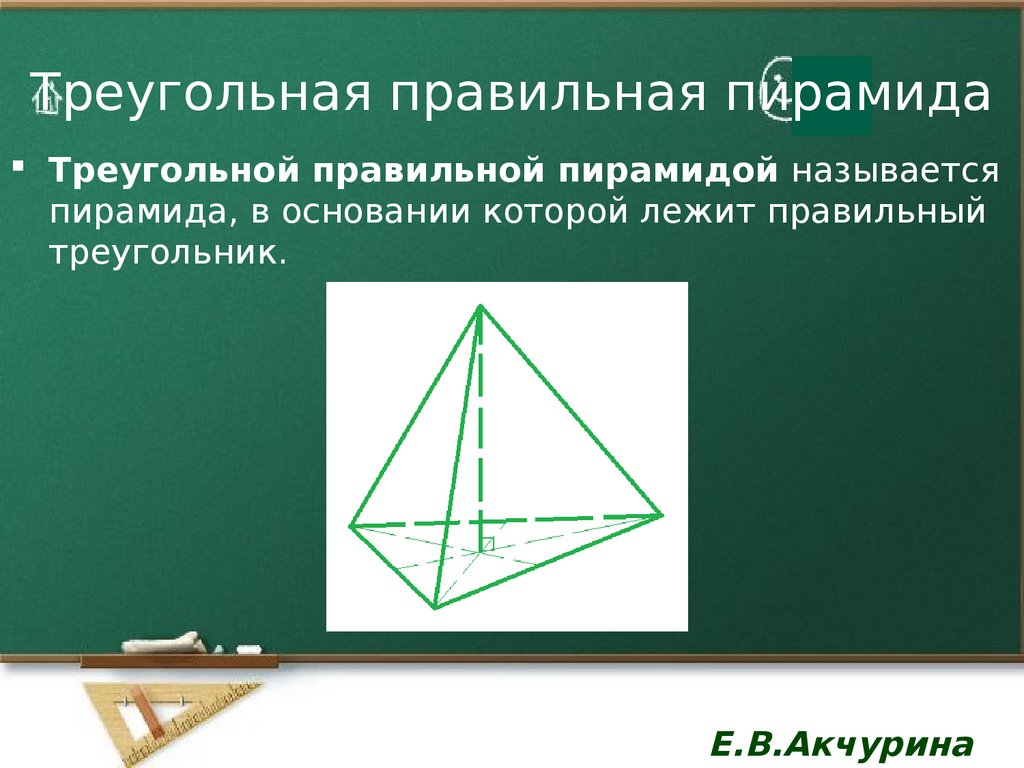

      правильным тетраэдром.

      Правильная четырехугольная пирамида

      • Основание – правильный четырехугольник ABCD, другими словами, квадрат.
      • Боковые грани – равные равнобедренные треугольники: AEB, BEC, CED и AED.
      • Проекция вершины E на основание – точка O, является точкой пересечения диагоналей квадрата ABCD.
      • EO – высота фигуры.
      • EN и EM – апофемы (всего их 4, на рисунке в качестве примера изображено только два).
      • Равные углы между боковыми ребрам/гранями и основанием указаны соответствующими буквами
        (α         и β).

      Правильная шестиугольная пирамида

      • Основание – правильный шестиугольник ABCDEF.
      • Боковые грани – равные равнобедренные треугольники: AGB, BGC, CGD, DGE, EGF и FGA.
      • Проекция вершины G на основание – точка O, является точкой пересечения диагоналей/биссектрис шестиугольника ABCDEF.
      • GO – высота пирамиды.
      • GN – апофема (всего их должно быть шесть).

      Свойства правильной пирамиды

      1. Все боковые ребра фигуры равны. Другими словами вершина пирамиды находится на одинаковом расстоянии от всех углов ее основания.
      2. Угол между всеми боковыми ребрами и основанием одинаковый.
      3. Все грани наклонены к основанию под одним и тем же углом.
      4. Площади всех боковых граней равны.
      5. Все апофемы равны.
      6. Вокруг пирамиды можно описать сферу, центром которой будет точка пересечения перпендикуляров, проведенных к серединам боковых ребер.
      7. В пирамиду можно вписать сферу, центром которой будет точка пересечения биссектрис, берущих начало в углах между боковыми ребрами и основанием фигуры.

      Примечание: Формулы для нахождения площади поверхности, а также объема пирамиды представлены в отдельных публикациях.

      ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

      Таблица знаков зодиака

      Нахождение площади трапеции: формула и примеры

      Нахождение длины окружности: формула и задачи

      Римские цифры: таблицы

      Таблица синусов

      Тригонометрическая функция: Тангенс угла (tg)

      Нахождение площади ромба: формула и примеры

      Нахождение объема цилиндра: формула и задачи

      Тригонометрическая функция: Синус угла (sin)

      Геометрическая фигура: треугольник

      Нахождение объема шара: формула и задачи

      Тригонометрическая функция: Косинус угла (cos)

      Нахождение объема конуса: формула и задачи

      Таблица сложения чисел

      Нахождение площади квадрата: формула и примеры

      Что такое тетраэдр: определение, виды, формулы площади и объема

      Нахождение объема пирамиды: формула и задачи

      Признаки подобия треугольников

      Нахождение периметра прямоугольника: формула и задачи

      Формула Герона для треугольника

      Что такое средняя линия треугольника

      Нахождение площади треугольника: формула и примеры

      Нахождение площади поверхности конуса: формула и задачи

      Что такое прямоугольник: определение, свойства, признаки, формулы

      Разность кубов: формула и примеры

      Степени натуральных чисел

      Нахождение площади правильного шестиугольника: формула и примеры

      Тригонометрические значения углов: sin, cos, tg, ctg

      Нахождение периметра квадрата: формула и задачи

      Теорема Фалеса: формулировка и пример решения задачи

      Сумма кубов: формула и примеры

      Нахождение объема куба: формула и задачи

      Куб разности: формула и примеры

      Нахождение площади шарового сегмента

      Что такое окружность: определение, свойства, формулы

      Треугольная пирамида | Найти объем и площадь поверхности (формулы)

      Написано

      Malcolm McKinsey

      Проверка по фактам

      Paul Mazzola

      Triangular Pyramid

      A Triangular Pyramid IS IS IS IS IS IS IS IS IS IS IS IS ARIMID ARIMID ARIMID . твердое тело – многогранник – с треугольным основанием и тремя треугольными гранями, сходящимися в вершине пирамиды.

      Основанием пирамиды может быть любая двухмерная геометрическая форма:

      • Треугольник

      • Прямоугольник

      • квадрат

      • Hexagon

      • Octagon

      .

      Так же, как у вас может быть треугольная пирамида, вы также можете иметь прямоугольную пирамиду, пятиугольную пирамиду и т. д.

      Как треугольные пирамиды получили свое название

      Великие пирамиды Египта в Гизе, например, являются квадратной пирамидой, потому что ее основание (дно) – квадрат. Треугольная пирамида – это пирамида с треугольным основанием.

      Triangular pyramid definition

      Triangular pyramid faces, edges, and vertices

      A triangular pyramid has:

      • Triangular base

      • 3 triangular faces

      • 6 edges

      • 4 vertices

      Triangular pyramid — грани, ребра и вершины

      Правильная треугольная пирамида

      Пирамида с равносторонним треугольным основанием – это правильная треугольная пирамида . Если в основании лежит разносторонний или равнобедренный треугольник, то пирамида представляет собой неправильная треугольная пирамида .

      Правильные и неправильные треугольные пирамиды

      Ни одно правило не требует, чтобы основание треугольной пирамиды было равносторонним треугольником, хотя построение разносторонних или равнобедренных треугольных пирамид намного сложнее, чем построение равносторонней треугольной пирамиды.

      Площадь поверхности треугольной пирамиды

      Для любого трехмерного тела можно выполнить два измерения площади поверхности: площадь боковой поверхности и площадь поверхности .

      Площадь боковой поверхности,  LSA , не включает основание нашей пирамиды. Площадь поверхности пирамиды SA включает основание.

      Треугольная пирамида – типы площадей

      Площадь поверхности треугольной пирамиды с тремя конгруэнтными видимыми гранями равна площади этих трех треугольных граней плюс площадь треугольного основания.

      Формула для расчета площади поверхности включает площадь основания, периметр основания и наклонную высоту любой стороны.

      Формула площади поверхности треугольной пирамиды

      Эта формула работает, потому что вы добавляете площадь основания к площади всех трех наклонных граней. Периметр дает вам сумму всех трех оснований. Вы умножаете эту сумму на высоту наклона треугольной пирамиды, как если бы у вас был один большой прямоугольник, а затем берете половину этой суммы как площадь трех треугольников.

      Как найти площадь поверхности треугольной пирамиды

      Предположим, у вас есть эта треугольная пирамида:

      Формула площади поверхности треугольной пирамиды

      Основанием пирамиды является равносторонний треугольник, поскольку все три его стороны равны 10 локтей.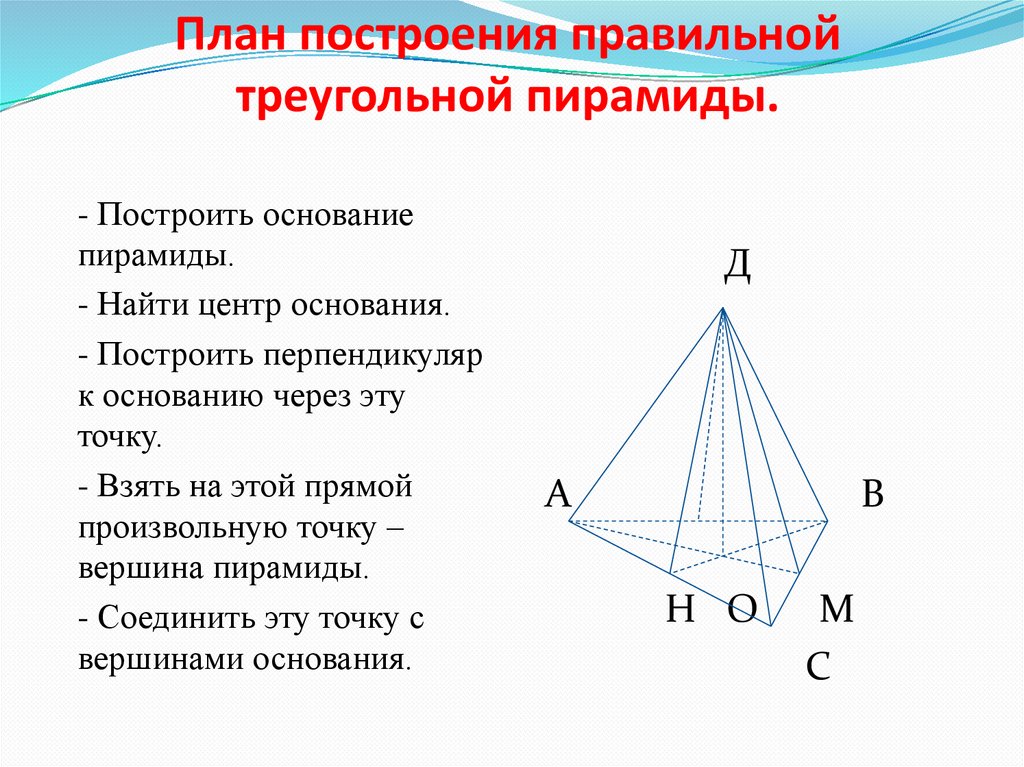 Чтобы найти площадь основания треугольника, используйте эту формулу для площади равностороннего треугольника со сторонами a :

      Для этой конкретной треугольной пирамиды формула работает как:

      Теперь мы нашли площадь основания . Мы уже знаем, что периметр основания равен 30 локтей (три стороны равны 9{2}локтей2.

      Как вычислить площадь боковой поверхности треугольной пирамиды

      Вам, возможно, потребовалось время, чтобы разобраться во всем этом, найти площадь основания, найти периметр, сложить все.

      Чтобы найти площадь только  наклонных сторон – площадь боковой поверхности ( LSA ) – нужно сделать намного меньше работы:

      Формула площади боковой поверхности для треугольной пирамиды

      Только эти формулы работа для обычных пирамид. Если у вас есть неправильная треугольная пирамида, вычислите площадь каждой из четырех граней по отдельности (три наклонных грани и основание) и сложите их вместе.

      Объем треугольной пирамиды

      Объем — это объем пространства, которое занимает трехмерное тело, поэтому для треугольной пирамиды мы находим, сколько места у нее внутри. Он всегда измеряется в кубических единицах. Хотя пирамида быстро сужается к вершине, вычисления несложны.

      Формула объема треугольной пирамиды

      В формуле объема треугольной пирамиды A  является площадью основания, а h  является высотой от основания до вершины.

      Треугольная пирамида — формула объема

      Для нашей пирамиды с основанием 10 локтей и наклонной высотой 14 локтей высота, h , получается 13,07690 1 локтей. Мы уже знаем площадь из наших предыдущих вычислений, поэтому мы можем подставить известные числа, чтобы получить объем в кубических локтях:

      Обратите внимание, что с дробью в нашем умножении у нас нет точного десятичного ответа , так что у нас есть приблизительное значение.

      Треугольная пирамида – формулы, примеры и диаграммы

      Определение

      Треугольная пирамида представляет собой многогранник с треугольным основанием, ограниченным тремя боковыми гранями, встречающимися в общей точке, известной как вершина.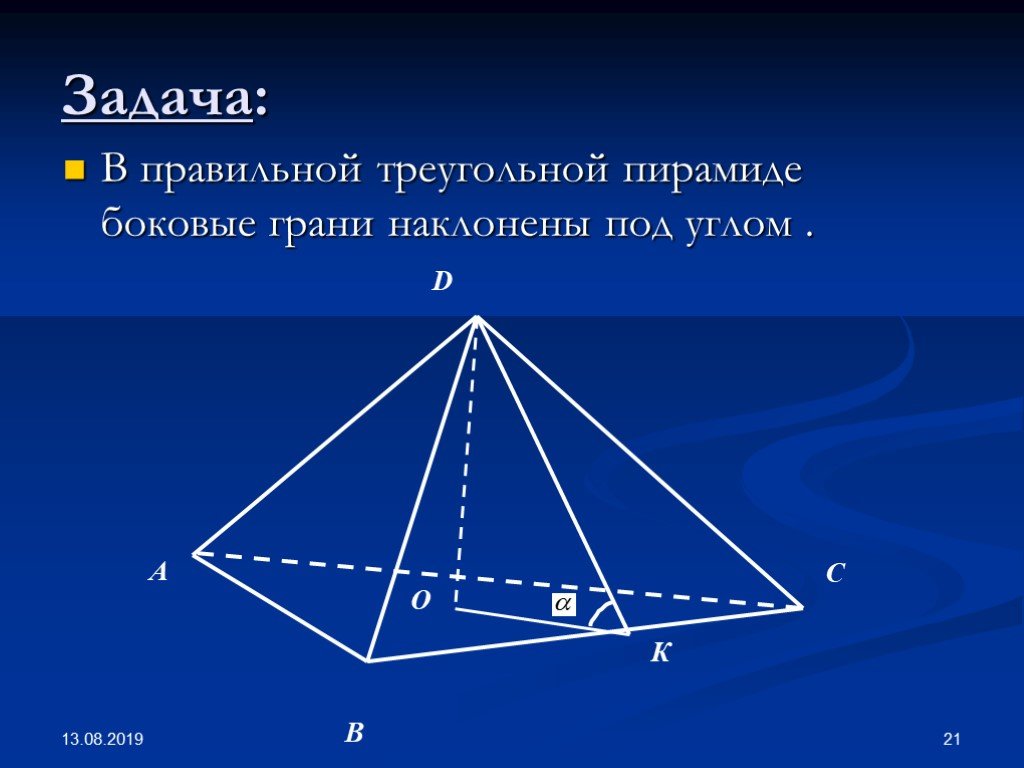

      Треугольная пирамида

      Боковые грани треугольные.

      Палатки и комбинированные головоломки — это реальный пример треугольной формы пирамиды.

      Сколько граней, вершин и ребер у треугольной пирамиды?

      Треугольная пирамида имеет 4 грани, 4 вершины и 6 ребер. Поскольку все 4 грани треугольные, треугольную пирамиду также называют тетраэдром .

      Сеть для треугольной пирамиды может проиллюстрировать ее форму в двухмерном виде. Эту сетку можно сложить по пунктирным линиям, чтобы сформировать треугольную пирамиду, как показано на рисунке ниже.

      Сеть треугольной пирамиды

      Типы

      В зависимости от правильности основания треугольная пирамида может быть – (1) Правильная треугольная пирамида , (2) Неправильная треугольная пирамида .

      Правильная

      Правильная треугольная пирамида – это пирамида, основание которой имеет форму равностороннего треугольника. Поэтому ее еще называют равносторонней треугольной пирамидой.

      Правильная треугольная пирамида

      Напротив, когда основание треугольной пирамиды неправильное, это неправильная треугольная пирамида .

      В зависимости от положения вершины треугольная пирамида может быть (1) Прямоугольной треугольной пирамидой , (2) Косая треугольная пирамида .

      Правосторонняя

      Прямоугольная пирамида — это пирамида, вершина которой находится прямо над центром основания. Итак, воображаемая линия, проведенная из вершины, пересекает основание в его центре под прямым углом. Эта линия является его высотой.

      Прямоугольная пирамида

      Напротив, когда вершина находится далеко от центра основания, пирамида представляет собой наклонную треугольную пирамиду .

      Как и все другие многогранники, мы можем вычислить площадь поверхности и объем треугольной пирамиды.

      Формулы

      Объем

      Формула:

      Объем ( V ) = ${\dfrac{1}{3}Bh}$, здесь B = площадь основания, h = высота

      Давайте решить некоторые примеры, включающие приведенную выше формулу.

      Найдите объем правильной треугольной пирамиды с площадью основания 97 см 2 и высотой 26 см.

      Решение:

      Как мы знаем,
      Объем ( V ) = ${\dfrac{1}{3}Bh}$, здесь B = 97 см 2 , h = 26 см
      ∴ В = ${\dfrac{1}{3}\times 97\times 26}$
      = 840,6 см 3

      4 Найдите объем прямоугольной треугольной пирамиды с основанием 21 см, высотой основания 8 см и высотой 17 см.

      Решение:

      Как мы знаем,
      Объем ( V ) = ${\dfrac{1}{3}Bh}$
      B = ${\dfrac {1}{2}bH}$, здесь b = основание, H = высота основания
      подставляя значение B, получаем,
      Объем ( V ) = ${\dfrac{1}{6}bHh}$ , здесь b = 21 см, H = 8 см, h = 17 см
      ∴ V = ${\dfrac{ 1}{6}\times 21\times 8\times 17}$
      = 476 см 3

      Нахождение объема правильной треугольной пирамиды, когда известны ОСНОВАНИЕ и ВЫСОТА 6

      Найдите объем правильной треугольной пирамиды с основанием 7 см и высотой 16 см.

      9{2}\times 16}$
      = 21,21762 × 1/3 × 16
      = 113,16 см 3

      Площадь поверхности

      Площадь поверхности (SA) = ${B+\dfrac{1}{2}Ps }$, здесь B = площадь основания, P = периметр основания, s = наклонная высота,

      Также ${\dfrac{1}{2}Ps}$ = площадь боковой поверхности ( LSA )  

      ∴  SA  = B + LSA

      Давайте решим несколько примеров, чтобы лучше понять приведенную выше концепцию.

      Найдите площадь поверхности правильной треугольной пирамиды с площадью основания 62,35 см 2 , периметр основания 36 см и высота наклона 7 см.

      Решение:

      Как известно,
      Общая площадь поверхности ( TSA ) = ${B+\dfrac{1}{2}Ps}$, здесь B = 62,35 см 2 , P = 36 см , s = 7 см
      ∴ TSA = ${62,35+\dfrac{1}{2}\times 36\times 7}$
      = 188,35 см 2

      Найти боковую и полную поверхности площадь треугольной пирамиды с основанием 8 см, высотой основания 4,6 см и высотой наклона 9 см.