4.4. Логические элементы и синтез логических схем. Информатика: аппаратные средства персонального компьютера
4.4. Логические элементы и синтез логических схем
Сложные цифровые логические устройства, входящие в состав компьютера, состоят из ряда элементарных логических элементов, построенных на базе средств электронной техники. При производстве этих электронных логических элементов используют различные технологии и схемотехнические решения, такие как: ДТЛ (диодно-транзисторная логика), ТТЛ (транзисторно-транзисторная логика), ЭСЛ (эмиттерно-связанная логика), технологии, основанные на использовании полевых транзисторов, и т. д. Логические элементы позволяют реализовать любую логическую функцию. Входные и выходные сигналы логических элементов, соответствующие двум логическим состояниям 1 и 0, могут иметь один из двух установленных уровней электрического напряжения, который зависит от схемотехнического решения логического элемента. Например, для логических элементов, основанных на технологии ТТЛ, высокий уровень электрического напряжения (2,4 ? 5 В) соответствует значению логической единицы (истина), а низкий уровень (0 ? 0,4 В) – логическому нулю (ложь).
Три приведенных ниже логических элемента составляют функционально полную систему для проектирования цифровых логических устройств, в том числе и соответствующих логических блоков и устройств компьютера, поскольку реализуют функционально полный набор логических функций, состоящий из логических функций: И (конъюнкции), ИЛИ (дизъюнкции), НЕ (отрицания).
1. Логический элемент НЕ, который называется также инвертором, выполняет логическую операцию отрицания (инверсии).
2. Логический элемент И, называемый также конъюнктором, выполняет операцию логического умножения (конъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.
3. Логический элемент ИЛИ, называемый также дизъюнктором, выполняет операцию логического сложения (дизъюнкции), теоретически может иметь бесконечное число входов, на практике ограничиваются числом входов от двух до восьми.
При проектировании цифровых логических устройств часто возникает задача по заданной таблице истинности записать выражение для логической функции и реализовать ее в виде логической схемы, состоящей из функционально полного набора логических элементов.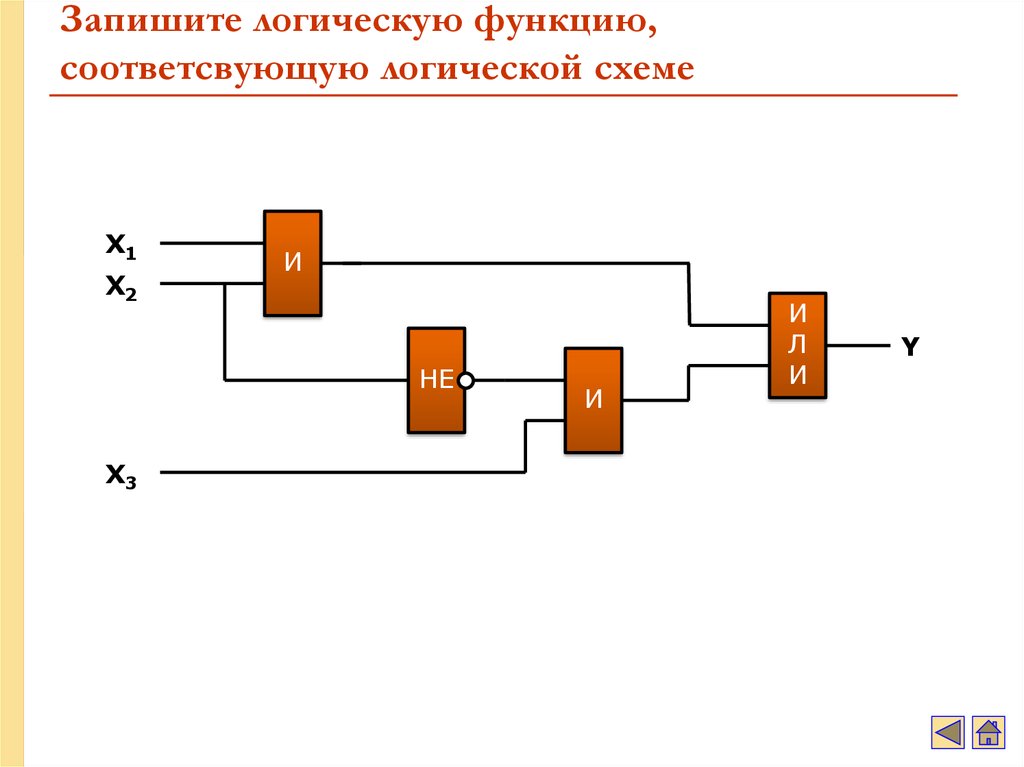 Данную задачу называют также задачей синтеза логических схем или логических устройств.
Данную задачу называют также задачей синтеза логических схем или логических устройств.
Синтез логических схем на основе функционально полного набора логических элементов состоит из представления логических функций, описывающих данные логические схемы в нормальных формах. Нормальной формой представления считается форма, полученная посредством суперпозиций вспомогательных логических функций – минтермов и макстернов.
Минтермом называют логическую функцию, которая принимает значение логической единицы только при одном значении логических переменных и значение логического нуля при других значениях логических переменных. Например, минтермами являются логические функции F2
Макстерном называют логическую функцию, которая принимает значение логического нуля только при одном значении логических переменных и значение логической единицы при других значениях логических переменных. Например, макстернами являются логические функции F8, F12, F14и F15(см.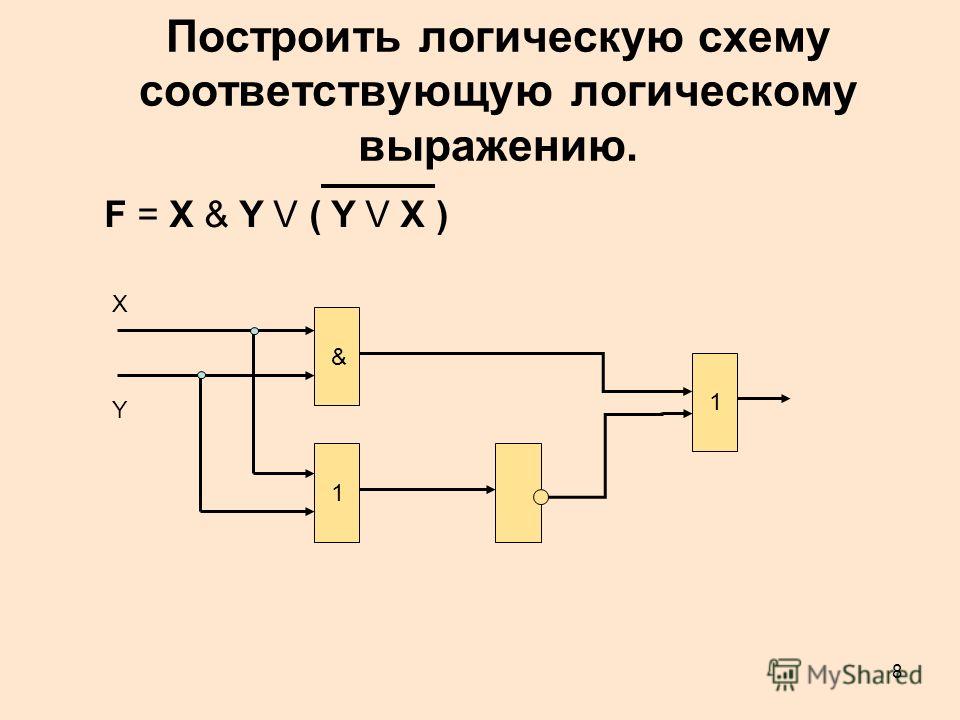 рис. 4.3).
рис. 4.3).
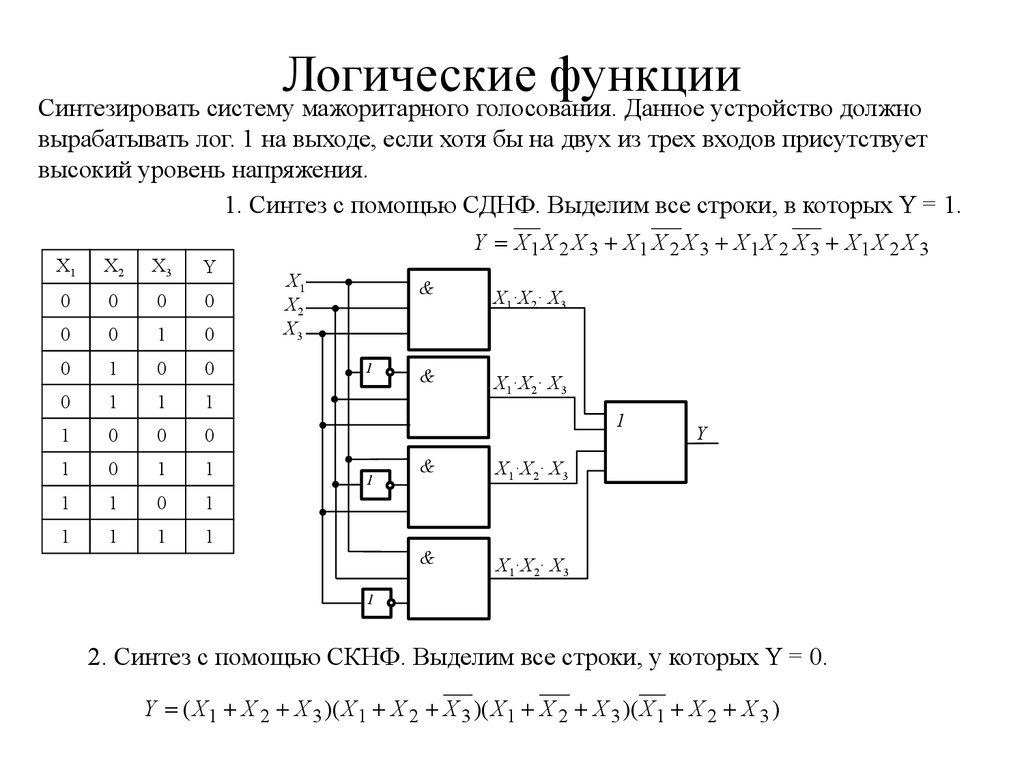
Из минтермов и макстернов методом суперпозиции можно составить логические функции, которые называются соответственно логической функцией, представленной посредством совершенных дизъюнктивных нормальных форм (СДНФ), и логической функцией, представленной посредством совершенных конъюнктивных нормальных форм (СКНФ). Полученные таким образом функции СДНФ и СКНФ будут представлять искомую логическую функцию по заданной таблице истинности. После получения функций СДНФ и СКНФ их необходимо преобразовать (минимизировать). Преобразование данных функций с целью их минимизации осуществляется с помощью законов алгебры логики и специальных разработанных методов: метод Квайна, карты Карно, диаграммы Вейча и т. д.
Рассмотрим задачу синтеза на примере модифицированной таблицы истинности, приведенной на рис. 4.6. Для данной таблицы истинности необходимо записать выражение для выходной функции F, провести ее преобразование (минимизацию) на основе законов алгебры логики и, используя основные логические элементы – НЕ, И и ИЛИ, разработать логическую схему реализации выходной функции 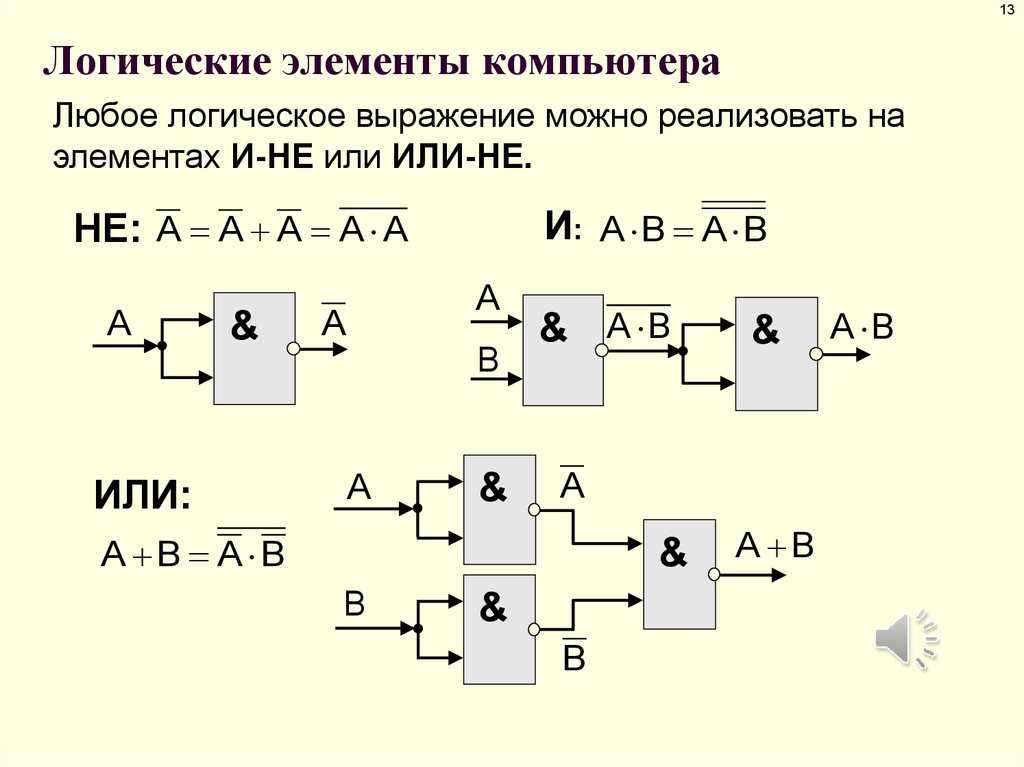
Рис. 4.6. Таблица истинности логических переменных A, В и С
Значения логических переменных А, В и С и соответствующие значения функции F приведены в таблице истинности (см. рис. 4.6), где в столбце № – указан номер комбинации логических переменных A, В и С.
Для решения указанной задачи представим логическую функцию F в виде СДНФ, а затем и в СКНФ. Найдем вспомогательные функции минтермы и макстермы. В заданной таблице истинности выходная функция
Минтермы запишем в следующем виде:
Минтермы представляют собой логические произведения (конъюнкции) логических переменных А, В, и С при значениях логической функции F, равных логической единице (комбинации 3, 6, 8).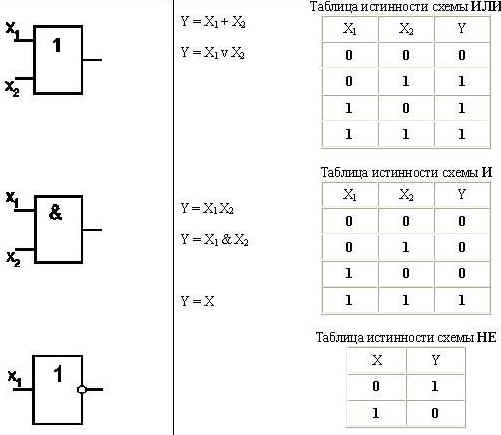 Сомножители (логические переменные
Сомножители (логические переменные
После минимизации логической функции Fc использованием законов алгебры логики получим ее искомое выражение:
Макстермы запишем в следующем виде:
Макстермы представляют собой логические суммы (дизъюнкции) логических переменных А, В, и С при значениях логической функции F, равных логическому нулю (комбинации 1, 2, 4, 5, 7). Слагаемые (логические переменные
Поскольку полученное выражение для F в виде СКНФ является более громоздким по сравнению с представлением F в виде СДНФ, то в качестве окончательного выражения для F примем ее выражение в виде СДНФ, т.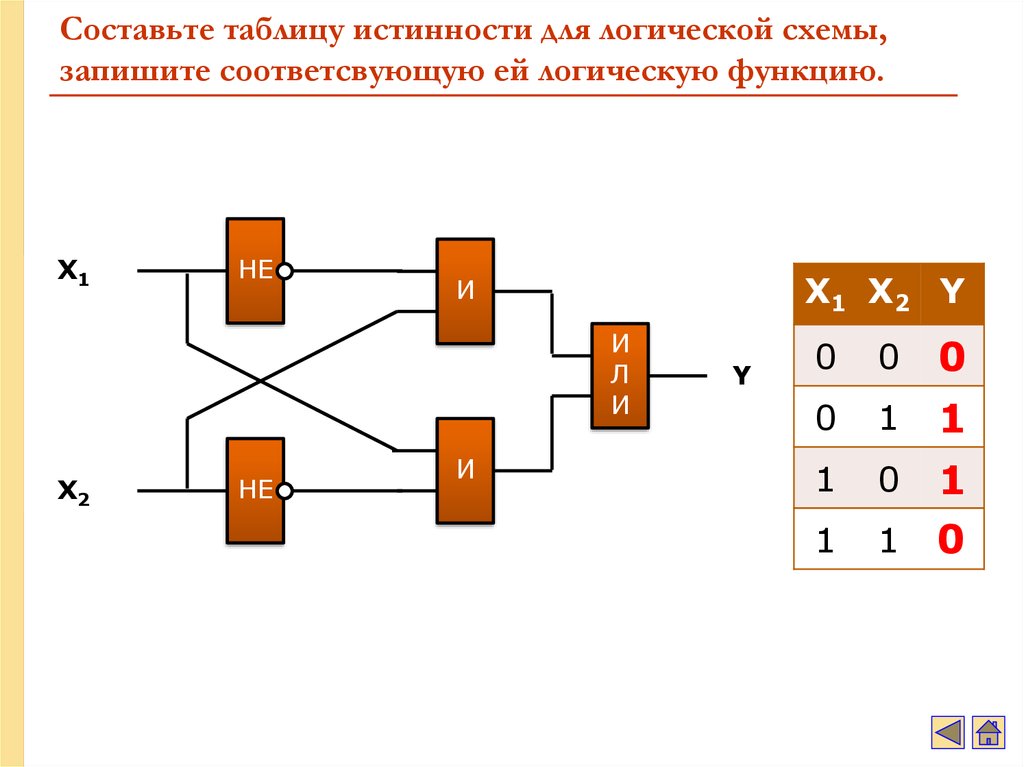 е.
е.
Аналогичным образом можно получить выражение для любой логической функции, которая представлена с помощью заданной таблицы истинности с Означениями логических переменных.
Используем полученное выражение логической функции F для разработки (построения) логической схемы на основе функционально полного набора логических элементов НЕ, И и ИЛИ. При построении логической схемы необходимо учитывать установленные в алгебре логики правила (приоритеты) для выполнения логических операций, которые в данном случае реализуются с помощью логических элементов НЕ, И и ИЛИ. Порядок производимых логических операций будет следующий: операция инверсии (отрицания), операция логического умножения (конъюнкции) и затем операция логического сложения (дизъюнкции). Реализация функции F в виде логической схемы, приведена на рис. 4.7.
Рис. 4.7. Реализация функции F в виде логической схемы
Для графического отображения логических схем существуют различные компьютерные программы, называемые графическими редакторами. Данные программы могут быть включены в другие компьютерные программы, например в программах Microsoft Word и Microsoft Excel такие редакторы реализованы с помощью панелей инструментов «Рисование», или быть самостоятельными программами, например Paint, Microsoft Visio и т. д. Воспользуемся встроенным графическим редактором (панель «Рисование») программы MS Excel для графического отображения логической схемы функции
Данные программы могут быть включены в другие компьютерные программы, например в программах Microsoft Word и Microsoft Excel такие редакторы реализованы с помощью панелей инструментов «Рисование», или быть самостоятельными программами, например Paint, Microsoft Visio и т. д. Воспользуемся встроенным графическим редактором (панель «Рисование») программы MS Excel для графического отображения логической схемы функции
Рис. 4.8. Графическое отображение логической функции F с помощью программы MS Excel
На основе функционально полного набора логических элементов построены различные электронные устройства, входящие в состав компьютера. К таким устройствам относятся сумматоры (выполняющие операции сложения двоичных чисел), триггеры (устройства, имеющие два устойчивых состояния: логического нуля и логической единицы и используемые в качестве двоичных элементов памяти), регистры памяти (состоящие из набора триггеров), двоичные счетчики, селекторы (переключатели сигналов), шифраторы, дешифраторы и т.
Рассмотренные выше таблицы истинности логических элементов показывают установившиеся значения логических переменных. Однако когда логические переменные представлены в виде электрических сигналов, то необходимо некоторое время для того, чтобы значение логической функции достигло уровня установившегося состояния из-за внутренних задержек по времени в электронных логических элементах. В среднем задержка электрического сигнала такого элемента составляет 10-9 с. В компьютере двоичные сигналы проходят через множество электронных схем, и задержка по времени может стать значительной. В этом случае выделяется отрезок времени (такт) на каждый шаг логической операции. Если операция заканчивается раньше, чем заканчивается тактовое время, то устройство, входящее в состав компьютера, ожидает ее окончания. В результате скорость выполнения операций несколько снижается, но достигается высокая надежность, так как обеспечивается синхронизация между многими параллельно выполняющимися операциями в компьютере. Синхронизация устройств в компьютере обеспечивается с помощью специального генератора – генератора тактовой частоты, который вырабатывает электрические импульсы стабильной частоты.
Синхронизация устройств в компьютере обеспечивается с помощью специального генератора – генератора тактовой частоты, который вырабатывает электрические импульсы стабильной частоты.
Данный текст является ознакомительным фрагментом.
Логические элементы для форматирования
Логические элементы для форматирования Как уже говорилось, логические элементы для форматирования определяют не внешний вид текста, а его тип, и в зависимости от которого браузер применяет тот или иной вид внешнего форматирования. Все элементы, рассматриваемые ниже,
5.5 Фильтрация и синтез изображений
5.5 Фильтрация и синтез изображений
Основной прием автоматизированной обработки изображений – фильтрация их целиком, либо выделенных в них областей. Большая часть упомянутых внешних модулей реализует именно функцию фильтрации. Среди наиболее важных в практической
Большая часть упомянутых внешних модулей реализует именно функцию фильтрации. Среди наиболее важных в практической
Диспетчер логических дисков
Диспетчер логических дисков Служба предназначена для обнаружения и наблюдения за работой новых жестких дисков. При этом все собираемые сведения передаются службе управления диспетчера логических дисков. Иными словами, если служба Диспетчер логических дисков
5.5 Фильтрация и синтез изображений
5.5 Фильтрация и синтез изображений Основной прием автоматизированной обработки изображений — фильтрация их целиком, либо выделенных в них областей. Большая часть упомянутых внешних модулей реализует именно функцию фильтрации. Среди наиболее важных в практической
Использование логических операций
Использование логических операций
Большинство инструментов выделения имеет одинаковые настройки, связанные с логическими операциями. Кнопки переключения режимов находятся слева на панели управления (рис. 16.7).
Рис. 16.7. Панель инструментов при работе с инструментом
Кнопки переключения режимов находятся слева на панели управления (рис. 16.7).
Рис. 16.7. Панель инструментов при работе с инструментом
Синтез звука и формат MIDI
Синтез звука и формат MIDI До настоящего момента речь шла об оцифровке и обработке реального звука, получаемого и записываемого с различных источников. Существует и совершенно иная задача – создание (синтез) звука на компьютере. Синтезатор – это набор управляемых
4.1. Логические переменные и логические операции
4.1. Логические переменные и логические операции Информация (данные, машинные команды и т. д.) в компьютере представлена в двоичной системе счисления, в которой используется две цифры – 0 и 1. Электрический сигнал, проходящий по электронным схемам и соединительным
6. Синтез текстов.
6. Синтез текстов. С проблемами поиска релевантного знания и понимания текстов весьма тесно соприкасается еще одна проблема, привлекающая сейчас внимание специалистов, работающих в ИИ. Она связана с разгадкой механизмов, лежащих в основе процедур порождения текстов на
§ 2.3 Элементы описания книги. Базовые структурные элементы
§ 2.3 Элементы описания книги. Базовые структурные элементы В самом начале любого файла книги идет признак формата XML<?xml version=»1.0″ encoding=»windows-1251″?>Здесь указана сигнатура принадлежности к формату XML, его версия и кодировка файла. Для русскоязычных FictionBook это обычно windows-1251
§ 2.4 Элементы описания книги (description). Элементы первого уровня
§ 2.4 Элементы описания книги (description). Элементы первого уровня
Элемент title-infoСодержит базовую информацию о книге (заголовок, информация об авторе и переводчике, аннотация, вхождение в серию и т. д.)Cинтаксис: <title-info>content</title-info>.Используется в элементах: descriptionВложенные
д.)Cинтаксис: <title-info>content</title-info>.Используется в элементах: descriptionВложенные
§ 2.5 Элементы описания книги (description). Элементы второго уровня
§ 2.5 Элементы описания книги (description). Элементы второго уровня Элемент genreЖанр произведения.Содержимое элемента строго фиксировано и определяется файлом FictionBookGenres.xsd, входящим в состав спецификации FictionBook.Список жанров с переводом приведен в Приложении В.Cинтаксис:
§ 2.6 Элементы описания книги (description). Элементы третьего уровня (информация об авторе)
§ 2.6 Элементы описания книги (description). Элементы третьего уровня (информация об авторе) Элемент first-nameИмя автора книги или документа, а также переводчика.Cинтаксис: <first-name>текст</first-name>Используется в элементах: author, translatorВложенные элементы: нетКоличество вхождений:
§ 2.
 8 Элементы раздела книги (section). Элементы первого уровня.
8 Элементы раздела книги (section). Элементы первого уровня.§ 2.8 Элементы раздела книги (section). Элементы первого уровня. Элемент citeЦитата. Отрывок текста из другого произведения.В FictionBook с помощью тэга cite также выделяются письма, записки, надписи, списки и еще много чего.Cинтаксис: <cite>content</cite>Используется в элементах: section,
§ 2.9 Элементы раздела книги (section). Элементы второго уровня.
§ 2.9 Элементы раздела книги (section). Элементы второго уровня. Элемент stanzaСтрофа стихотворения.Cинтаксис: stanza>content</stanza>Используется в элементах: poemВложенные элементы: title, subtitle, vКоличество вхождений: одно и болееАтрибуты: нетВерсия формата: 2.0Пример: см. пример
§ 2.11 Элементы абзаца (стилевые, они же inline элементы)
§ 2. 11 Элементы абзаца (стилевые, они же inline элементы)
Элемент aСсылка или сноска.Cинтаксис: <a>content</a>Используется в элементах: code, emphasis, p, strikethrough, strong, style, subtitle, sub, sup, th, td, vВложенные элементы: code, emphasis, strikethrough, strong, style, sub, sup, imageКоличество вхождений:
11 Элементы абзаца (стилевые, они же inline элементы)
Элемент aСсылка или сноска.Cинтаксис: <a>content</a>Используется в элементах: code, emphasis, p, strikethrough, strong, style, subtitle, sub, sup, th, td, vВложенные элементы: code, emphasis, strikethrough, strong, style, sub, sup, imageКоличество вхождений:
Синтез звука: сказки и сказочники
Синтез звука: сказки и сказочники Автор: Павел ЗолинОпубликовано 23 января 2012 годаОх уж эти сказки, ох уж эти сказочники! Ох уж эти синтезаторы, ох уж эти инженеры! Людей, так или иначе задействованных в синтезаторостроении, впору ненавидеть, потому что они используют нас,
Элементы схемотехники. Логические схемы
Информатика. 10 класса. Босова Л.Л. Оглавление
§ 21. Элементы схемотехники. Логические схемы
Элементы схемотехники.
 Логические схемы
Логические схемыЛюбое устройство компьютера, выполняющее арифметические или логические операции, может рассматриваться как преобразователь двоичной информации: значения входных переменных для него — последовательность нулей и единиц, а значение выходной функции — новая двоичная последовательность. Необходимые преобразования информации в блоках компьютера производятся логическими устройствами двух типов: комбинационными схемами и цифровыми автоматами с памятью.
В комбинационной схеме набор выходных сигналов в любой момент времени полностью определяется набором входных сигналов.
В цифровых автоматах с памятью набор выходных сигналов зависит не только от набора входных сигналов, но и от внутреннего состояния данного устройства. Такие устройства всегда имеют память.
Схемотехника — научно-техническое направление, занимающееся проектированием, созданием и отладкой электронных схем и электронных устройств различного назначения.
21.1. Логические элементы
Логический элемент — это устройство с л входами и одним выходом, которое преобразует входные двоичные сигналы в двоичный сигнал на выходе.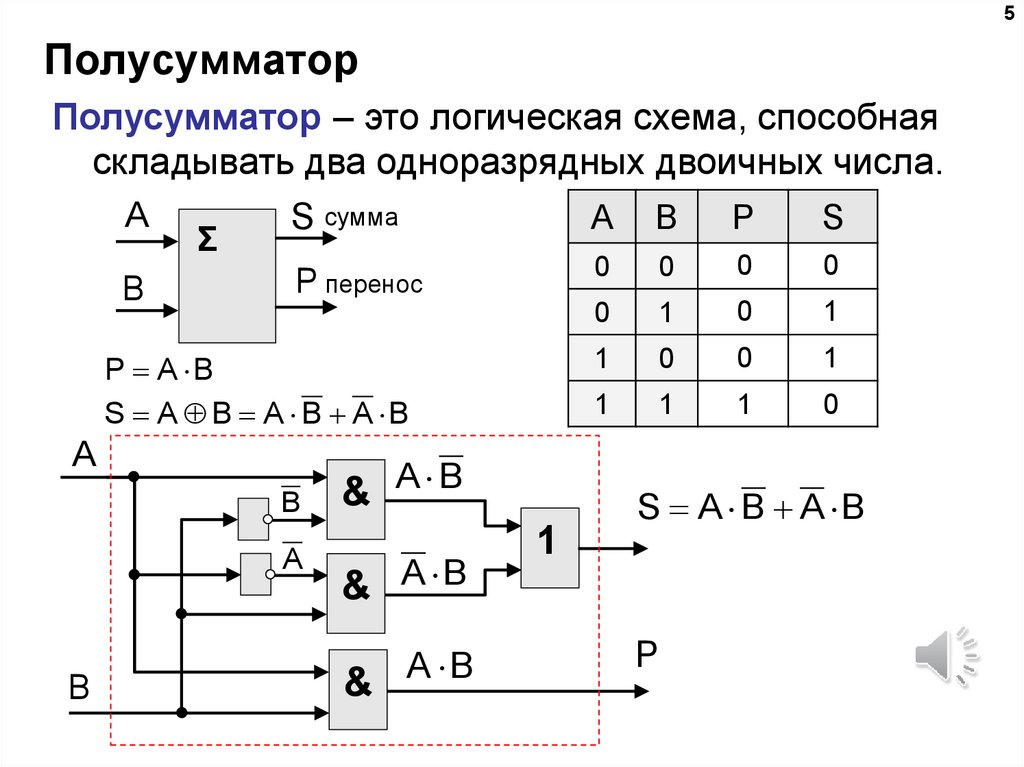
Работу любого логического элемента математически удобно описать как логическую функцию, которая упорядоченному набору из нулей и единиц ставит в соответствие значение, также равное нулю или единице.
В схемотехнике широко используются логические элементы, представленные в таблице 4.2.
Таблица 4.2
Условные обозначения типовых логических элементов
Логический элемент И (конъюнктор) реализует операцию логического умножения. Единица на выходе этого элемента появится тогда и только тогда, когда на всех входах будут единицы.
Опишите подобным образом логические элементы ИЛИ (дизъюнктор), НЕ (инвертор), И-НЕ, ИЛИ-НЕ.
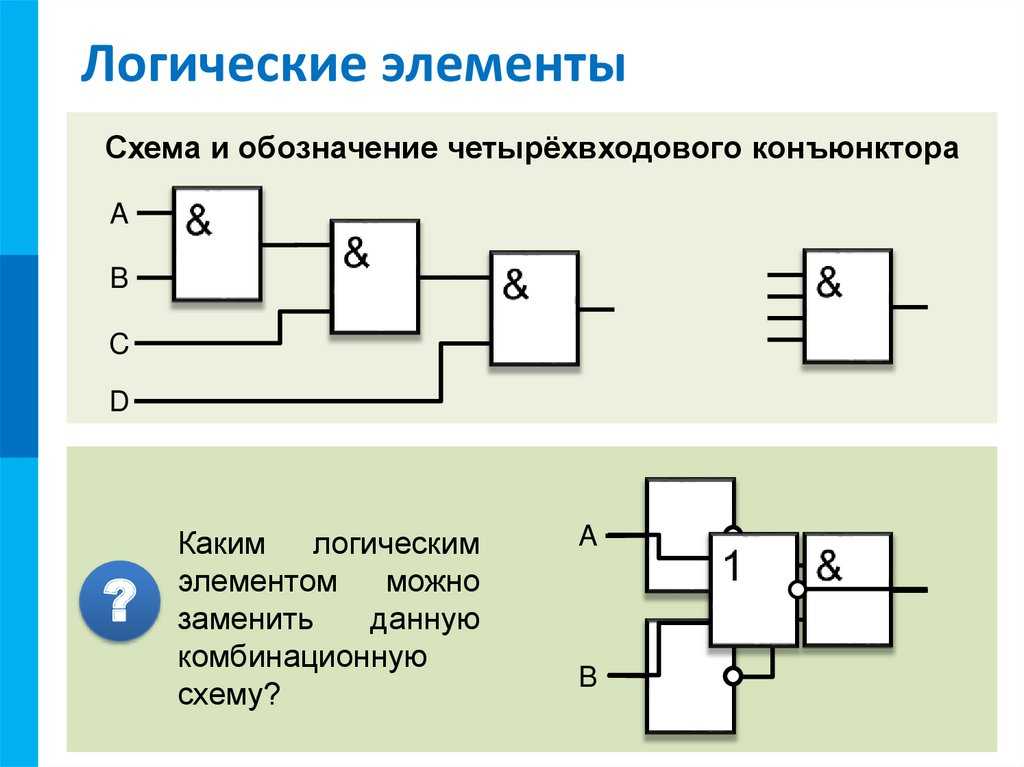
Однотипность сигналов на входах и выходах позволяет подавать сигнал, вырабатываемый одним элементом, на вход другого элемента. Это позволяет из двухвходовых элементов «собирать» многовходовые элементы (рис 4.7), а также синтезировать произвольные комбинационные схемы, соединяя в цепочки отдельные логические элементы.
Рис. 4.7. Схема и обозначение четырёхвходового конъюнктора
Пример. По заданной логической функции F(A, В) = & В v А & построим комбинационную схему (рис. 4.8).
Построение начнём с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе логической схемы должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые в свою очередь подаются один входной сигнал нормальный и один инвертированный (с инверторов).
Рис. 4.8. Комбинационная схема функции F(A, В) = & В v А &
21.2. Сумматор
Из отдельных логических элементов можно составить устройства, производящие арифметические операции над двоичными числами.
Электронная логическая схема, выполняющая суммирование двоичных чисел, называется сумматором.
Вспомним схему сложения двух n-разрядных двоичных чисел (рис. 4.9).
4.9).
Рис. 4.9. Схема сложения двух n-разрядных двоичных чисел
Заметим, что при сложении цифр в i-м разряде мы должны сложить цифру ai числа а, цифру bi числа b, а также рi — перенос из (i — 1)-го разряда. В результате сложения должны получиться цифра результата si и цифра переноса (0 или 1) в следующий разряд pi+1.
Основываясь на этих рассуждениях, построим таблицу истинности для функций, которые в зависимости от цифр ai, bi и pi получают цифры si и pi+l.
Вам известен алгоритм построения логического выражения по таблице истинности. Воспользуемся им и запишем выражение для функции pi+1:
Попытаемся упростить это выражение, воспользовавшись тем, что A v А = А. Основываясь на этом законе, включим в имеющуюся дизъюнкцию ещё два слагаемых вида ai & bi & pi, причём на основании коммутативного и ассоциативного законов преобразуем полученное выражение к виду:
Полученное выражение означает, что функция рi+1 принимает значение 1 только для таких комбинаций входных переменных, когда хотя бы две переменные имеют единичные значения. Обратите внимание на то, что такой вывод можно сделать и в результате анализа таблицы истинности.
Обратите внимание на то, что такой вывод можно сделать и в результате анализа таблицы истинности.
По таблице истинности можем записать выражение для si:
Его также можно попытаться преобразовать к более короткому виду. Но можно пойти другим путём и провести более тщательный анализ таблицы истинности для функции si.
Из таблицы видно, что значение si равно 1, если все входные сигналы равны 1. Этому соответствует выражение ai & bi & pi = 1.
Или значение si равно 1, если в комбинации входных сигналов есть единственная 1, т. е. единица среди переменных есть, но нет одновременно двух переменных, значения которых равны
1. Это можно записать так:
Следовательно, s,- можно записать так:
Можно попытаться самостоятельно провести преобразование логического выражения, полученного по таблице истинности для si к итоговому виду. Но, чтобы убедиться в равносильности этих двух выражений, достаточно построить таблицу истинности для второго из них.
Полученные выражения позволяют реализовать одноразрядный двоичный сумматор схемой, представленной на рисунке 4.10.
Рис. 4.10. Схема одноразрядного сумматора
Выразить si и pi+1 можно и другими формулами. Например, самое короткое выражение для si имеет вид: si = ai ? bi ? pi, что позволяет построить сумматор, используя другие логические элементы.
Сложение n-разрядных двоичных чисел осуществляется с помощью комбинации одноразрядных сумматоров (условное обозначение одноразрядных сумматоров приведено на рисунке слева).
21.3. Триггер
Триггер (от англ. trigger — защёлка, спусковой крючок) — логический элемент, способный хранить один разряд двоичного числа.
Триггер был изобретён в 1918 году М. А. Бонч-Бруевичем.
Михаил Александрович Бонч-Бруевич (1988-1940) — русский и советский радиотехник, основатель отечественной радиоламповой промышленности. Работал в области радиовещания и дальней связи на коротких волнах. В 1918 году М. А. Бонч-Бруевич предложил схему переключающего устройства, имеющего два устойчивых рабочих состояния, под названием «катодное реле». Это устройство впоследствии было названо триггером.
Работал в области радиовещания и дальней связи на коротких волнах. В 1918 году М. А. Бонч-Бруевич предложил схему переключающего устройства, имеющего два устойчивых рабочих состояния, под названием «катодное реле». Это устройство впоследствии было названо триггером.Самый простой триггер — RS. Он состоит из двух логических элементов ИЛИ-HE, входы и выходы которых соединены кольцом: выход первого соединён со входом второго и выход второго — со входом первого. Схема RS-триггера представлена на рисунке 4.11.
Рис. 4.11. Логическая схема RS-триггера
Триггер имеет два входа: S (от англ. set — установка) и R (от англ. reset — сброс) и два выхода: Q (прямой) и (инверсный). Принцип его работы иллюстрирует следующая таблица истинности:
Если на входы поступают сигналы R = 0 и S = O, то триггер находится в режиме хранения — на выходах Q и сохраняются установленные ранее значения.
Если на установочный вход S на короткое время поступает сигнал 1, то триггер переходит в состояние 1 и после того, как сигнал на входе S станет равен 0, триггер будет сохранять это состояние, т.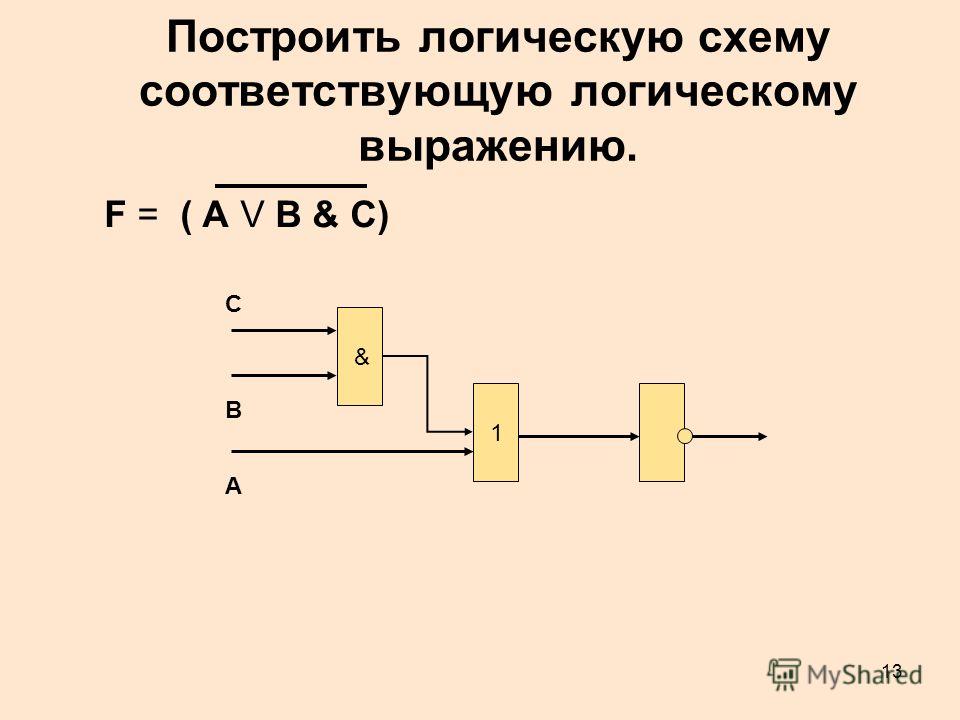 е. будет хранить 1.
е. будет хранить 1.
При подаче 1 на вход R триггер перейдёт в состояние 0.
Подача на оба входа S и R логической единицы может привести к неоднозначному результату, поэтому такая комбинация входных сигналов запрещена.
Триггер используется для хранения информации в оперативной памяти компьютера, а также во внутренних регистрах процессора. Для хранения одного байта информации необходимо 8 триггеров, для килобайта — 8 • 1024 триггеров. Оперативная память современных компьютеров содержит миллионы триггеров.
В целом же компьютер состоит из огромного числа логических устройств, образующих все его узлы и память.
САМОЕ ГЛАВНОЕ
Необходимые преобразования информации в блоках компьютера производятся логическими устройствами двух типов: комбинационными схемами и цифровыми автоматами с памятью.
В комбинационной схеме набор выходных сигналов в любой момент времени полностью определяется набором входных сигналов. Дискретный преобразователь, который выдаёт после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом. Электронная логическая схема, выполняющая суммирование двоичных чисел, называется сумматором.
Электронная логическая схема, выполняющая суммирование двоичных чисел, называется сумматором.
В цифровых автоматах с памятью набор выходных сигналов зависит не только от набора входных сигналов, но и от внутреннего состояния данного устройства. Такие устройства всегда имеют память. Триггер — логический элемент, способный хранить один разряд двоичного числа. Оперативная память современных компьютеров содержит миллионы триггеров.
В целом же компьютер состоит из огромного числа логических устройств, образующих все его узлы и память.
Вопросы и задания
1. Что такое логический элемент? Перечислите базовые логические элементы?
2. По логическому выражению требуется разработать логическое устройство. Какие логические элементы необходимы для его создания?
3. Найдите значение выходного сигнала в приведенной схеме, если
4. Определите логическое выражение преобразования, выполняемого схемой:
5.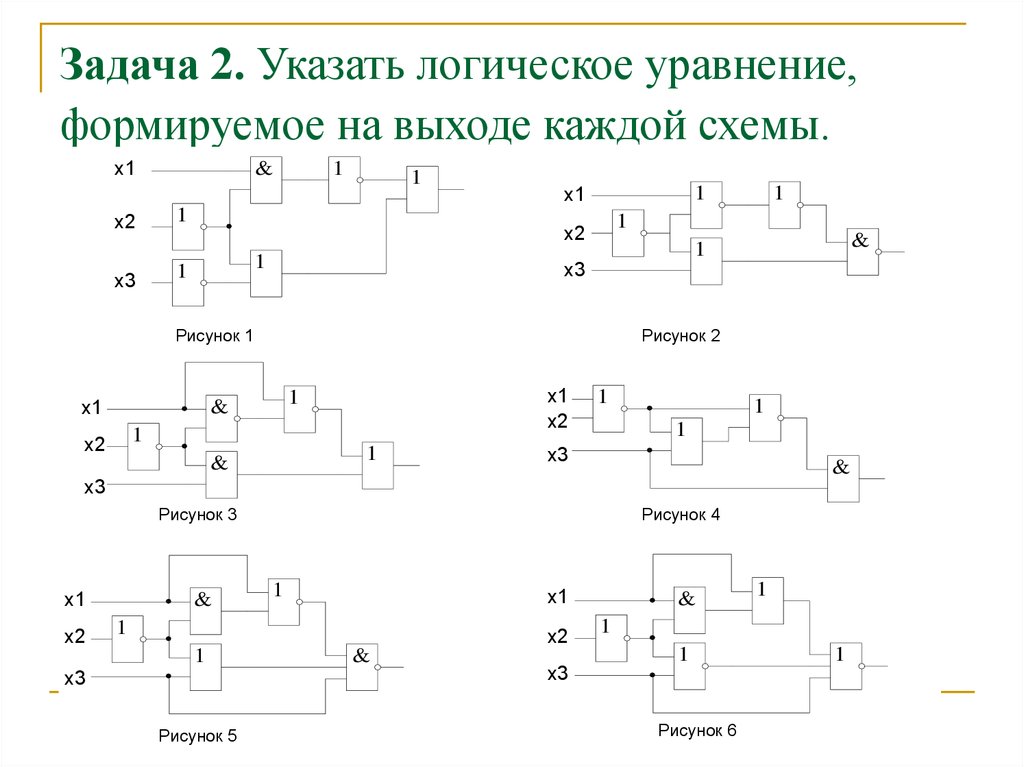 Постройте логические схемы для следующих функций:
Постройте логические схемы для следующих функций:
6. Постройте схему устройства, выполняющего преобразование информации в соответствии с данной таблицей истинности:
7. Пусть в некотором конкурсе вопрос о допуске того или иного участника к следующему туру решается тремя членами жюри: А, В и С. Решение положительно тогда и только тогда, когда хотя бы двое членов жюри высказываются за допуск, причём среди них обязательно должен быть председатель жюри А. Необходимо разработать устройство для голосования, в котором каждый член жюри нажимает на одну из двух кнопок — «За» или «Против», а результат голосования всех трёх членов жюри определяется по тому, загорится (участник допускается) или нет (участник не допускается) сигнальная лампочка. Составьте схему устройства, которое на выходе выдавало бы 1, если участник допускается к следующему туру, и 0, если не допускается.
8. Существует 16 логических устройств, имеющих два входа (16 логических функций от двух переменных).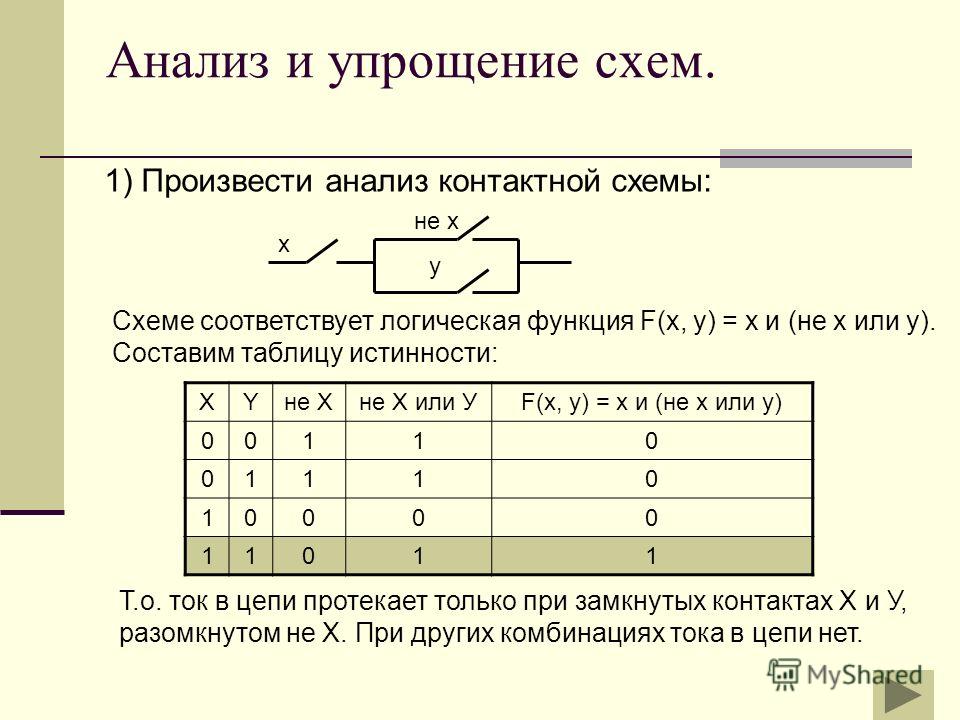 Реализуйте их комбинационные схемы с помощью логических элементов И, ИЛИ, НЕ.
Реализуйте их комбинационные схемы с помощью логических элементов И, ИЛИ, НЕ.
9. Если при суммировании не учитывается признак переноса, то соответствующая логическая схема называется полусумматором. По имеющейся таблице истинности постройте логическую схему полусумматора.
10. Что такое триггер? В чём основное отличие триггера от таких логических элементов, как инвертор или конъюнктор?
11. Подготовьте краткую биографическую справку о нашем выдающемся соотечественнике М. А. Бонч-Бруевиче. В чём заключается его вклад в развитие вычислительной техники?
§ 20. Преобразование логических выражений
§ 21. Элементы схемотехники. Логические схемы
§ 22. Логические задачи и способы их решения
Логическая схема, показанная ниже, имеет входные сигналы A и B, как показано. Выберите правильную форму выходного сигнала.
NCERT CENTIPS -SECEMONDUCTOR ЭЛЕКТРОНИКА: Материалы, устройства и простые схемы -Дигитальная электроника и логическая ворота
16 ВидеоРеклама
AB Padhai Karo Bina Ads KE
KHAREEDO DN PRO и DEKHO SARI VIDEOS BINA KINAVATAVAT!
Дата обновления: 27 июня 2022 г.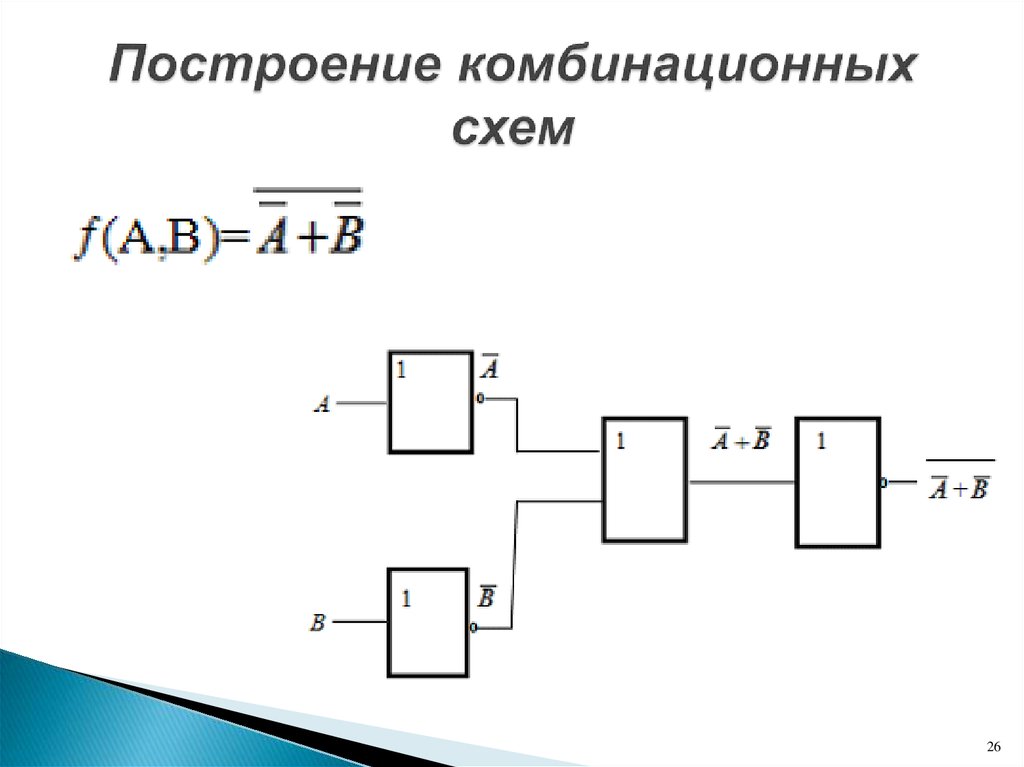
Текстовое решение
A
B
C
D
Ответ
Правильный ответ A
Решение
Выход схемы: ¯¯¯B=¯¯¯¯¯¯¯¯A.¯¯¯¯¯¯B=A.B (по теореме де Моргана)
Это логическое выражение вентиля AND.
Форма выходного сигнала, соответствующая заданным входным сигналам A и B, показана ниже.
Ответ
Пошаговое решение, разработанное экспертами, чтобы помочь вам избавиться от сомнений и получить отличные оценки на экзаменах.
Видео по теме
Показанная ниже логическая схема имеет входные сигналы «A» и «B», как показано на рисунке. Выберите правильную форму выходного сигнала
13157211
Текст Решение
Показанная ниже логическая схема имеет входные сигналы «A» и «B», как показано на рисунке. Выберите правильную форму выходного сигнала.
13165731
Показанная ниже логическая схема имеет форму входного сигнала «A» и «B», как показано на рисунке.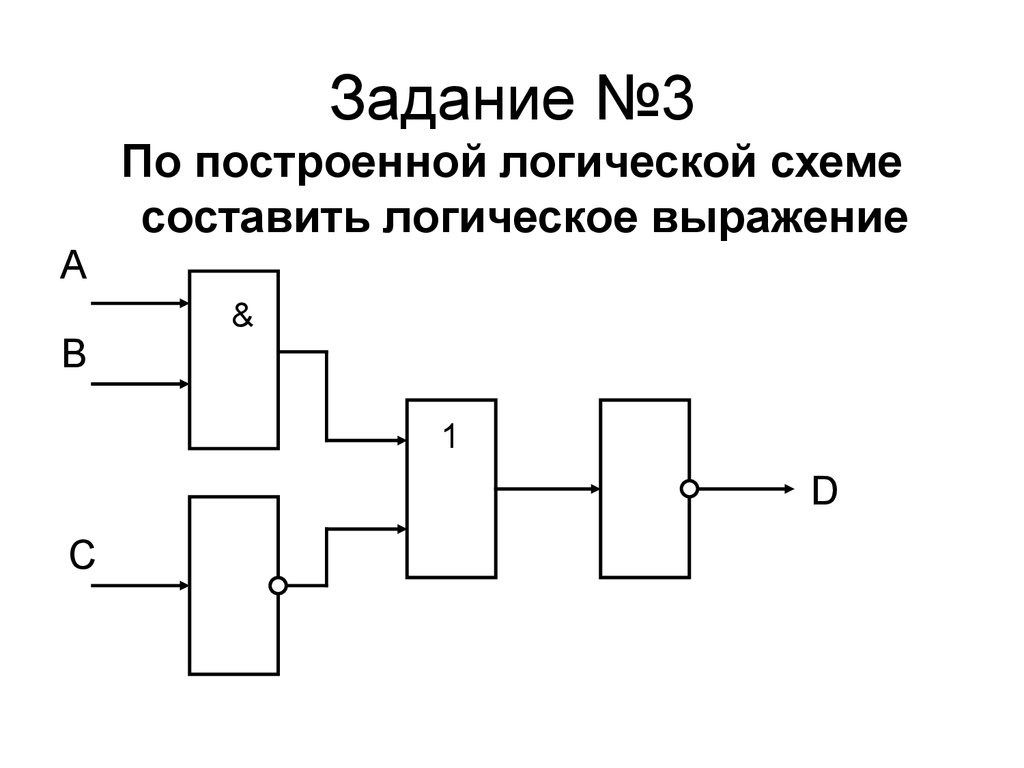 Выберите правильную форму выходного сигнала Выход: —
Выберите правильную форму выходного сигнала Выход: —
14533912
Показанная логическая схема имеет входные сигналы «A» и «B», как показано. Выберите ПРАВИЛЬНУЮ форму выходного сигнала: —
14626561
Логическая схема, показанная ниже, имеет входные сигналы «A» и «B», как показано на рисунке. Выберите правильную форму выходного сигнала
14930888
Два входных сигнала A и B, показанные на рис. (a), подаются на логический элемент И. Запишите форму выходного сигнала.
17959604
На следующем рисунке показана схема логического элемента с двумя входами A и B и выходом C. Формы сигналов напряжения A, B и C показаны ниже.
Элемент логической схемы
95417275
Показанная логическая схема имеет входные сигналы «A» и «B», как показано. Выберите правильную форму выходного сигнала
111268685
Показанная ниже логическая схема имеет входные сигналы «A» и «B», как показано на рисунке.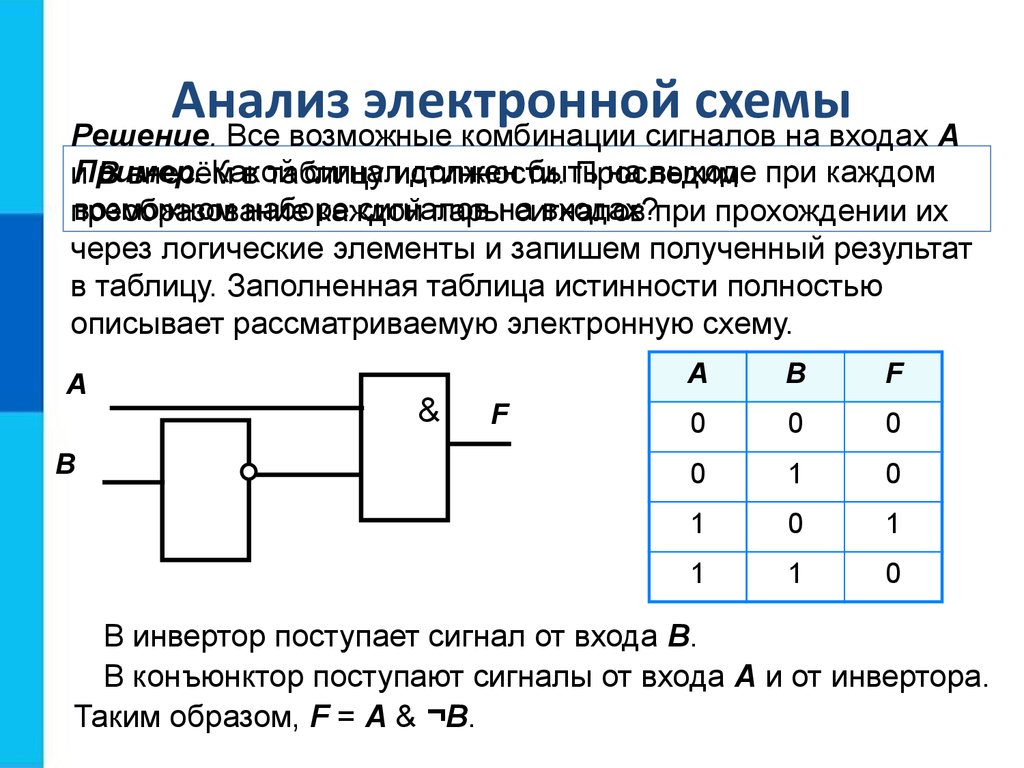 Выберите правильную форму выходного сигнала.
Выберите правильную форму выходного сигнала.
Выход
:
415585835
Ниже показана схема логического элемента с двумя входами A и B и выходом C. Формы сигналов напряжения A, B и C показаны ниже.
Элемент логической схемы
548483890
Показанная ниже логическая схема имеет входные сигналы «A» и «B», как показано на рисунке. Выберите правильную форму выходного сигнала
.
642609525
Показанная ниже логическая схема имеет входные сигналы A и B, как показано. Выберите правильную форму выходного сигнала.
642733428
Показанная ниже логическая схема имеет входные сигналы A и B, как показано. Выберите правильную форму выходного сигнала.
642751839
Показанная ниже логическая схема имеет входные сигналы «A» и «B», как показано. Выберите текущую выходную форму волны.
642854343
Показанная ниже логическая схема имеет форму входного сигнала «A» и «B», как показано.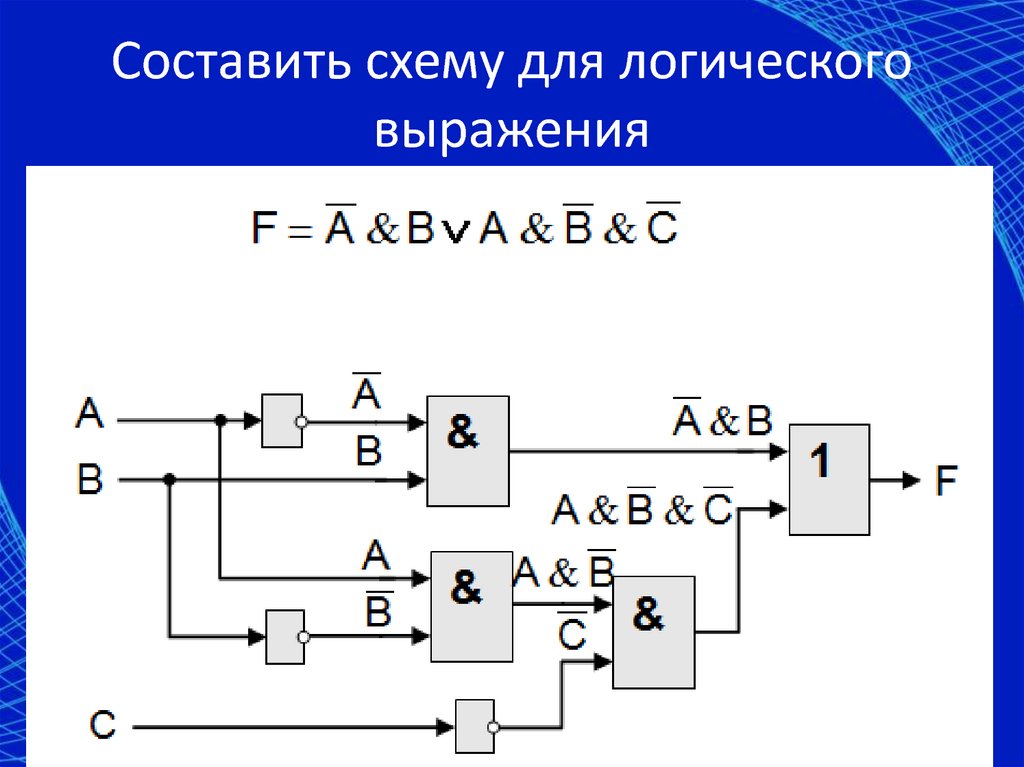 Выберите правильную форму выходного сигнала
Выберите правильную форму выходного сигнала
.
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 6710
- Кэрол Кричлоу и Дэвид Дж. Эк
- Колледжи Хобарта и Уильяма Смита
- 9
- Используя только вентили и, или, но не элементы, нарисуйте схемы, вычисляющие значение каждого из предложений A → B, A ↔ B и A ⊕ B.
- Для каждого из следующих предложений найдите комбинаторную логическую схему, которая вычисляет это предложение: p∧¬q)\)
c) \((p∨q∨r)∧(¬p∨¬q∨¬r)\)
d) \(¬(A∧(B∨C) )∨(B∧¬A)\) - Найдите составное предложение, вычисленное каждой из следующих схем:
- В этом разделе описывается метод нахождения составного предложения, вычисляемого любой комбинаторной логической схемой.
 Этот метод не работает, если вы попытаетесь применить его к схеме, содержащей петлю обратной связи. Что пойдет не так? Приведите пример.
Этот метод не работает, если вы попытаетесь применить его к схеме, содержащей петлю обратной связи. Что пойдет не так? Приведите пример. - Покажите, что каждое составное предложение, не являющееся противоречием, эквивалентно предложению в дизъюнктивной нормальной форме. (Примечание: мы можем снять ограничение, заключающееся в том, что составное предложение не является противоречием, согласившись с тем, что «F» считается предложением в дизъюнктивной нормальной форме. F логически эквивалентно любому противоречию.)
- Предложение в конъюнктивной нормальной форме (КНФ) представляет собой конъюнкцию дизъюнкций простых терминов (с оговоркой, как и в определении ДНФ, что один элемент считается конъюнкцией или дизъюнкцией). Покажите, что каждое сложное предложение, не являющееся тавтологией, логически эквивалентно сложному предложению в конъюнктивной нормальной форме. (Подсказка: что произойдет, если вы возьмете отрицание предложения ДНФ и примените законы ДеМоргана?)
- Предложение в конъюнктивной нормальной форме (КНФ) представляет собой конъюнкцию дизъюнкций простых терминов (с оговоркой, как и в определении ДНФ, что один элемент считается конъюнкцией или дизъюнкцией).
 Покажите, что каждое сложное предложение, не являющееся тавтологией, логически эквивалентно сложному предложению в конъюнктивной нормальной форме. (Подсказка: что произойдет, если вы возьмете отрицание предложения ДНФ и примените законы ДеМоргана?)
Покажите, что каждое сложное предложение, не являющееся тавтологией, логически эквивалентно сложному предложению в конъюнктивной нормальной форме. (Подсказка: что произойдет, если вы возьмете отрицание предложения ДНФ и примените законы ДеМоргана?) - Разработайте схемы для реализации таблиц ввода/вывода для добавления, как показано на рис. 1.8. Постарайтесь сделать ваши схемы максимально простыми. (Схемы, которые используются в реальных компьютерах для этой цели, более упрощены, чем те, которые вы, вероятно, придумаете, но общий подход использования логики для проектирования компьютерных схем верен.)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Кэрол Кричлоу и Дэвид Дж.

- 9
Компьютеры имеют репутацию — не всегда заслуженную — за то, что они «логичны». Но в основе своей, глубоко внутри, они сделаны из логики в самом прямом смысле. Строительные блоки компьютеров логические вентили , которые представляют собой электронные компоненты, вычисляющие значения простых предложений, таких как \(p ∧ q и ¬p\). (Каждый затвор, в свою очередь, состоит из электронных компонентов еще меньшего размера, называемых транзисторами, но здесь нас это не должно касаться.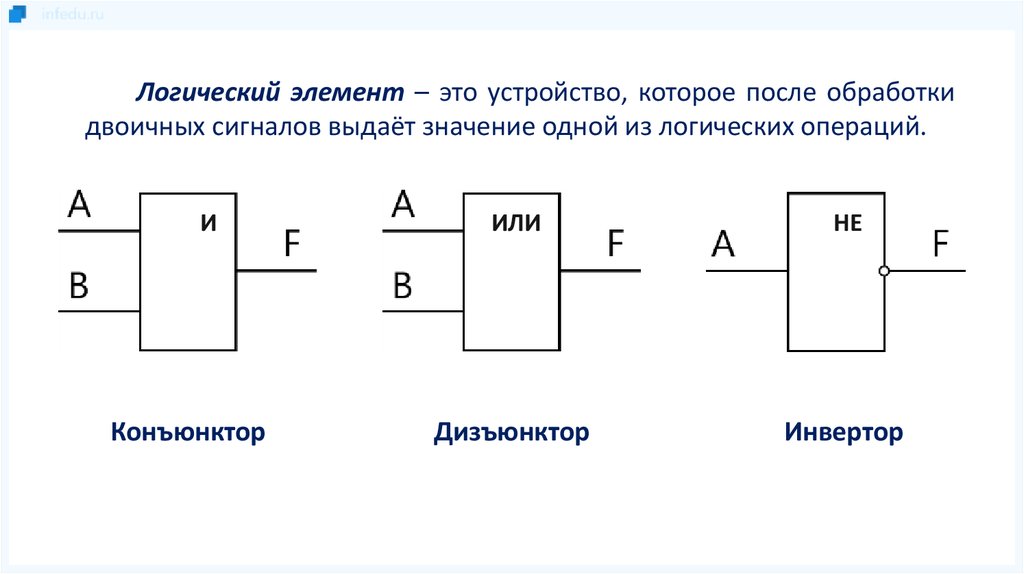 )
)
Провод в компьютере может находиться в одном из двух состояний, которые мы можем представить как на и на . Эти два состояния могут быть естественным образом связаны с булевыми значениями \(\mathbb{T}\) и \(\mathbb{F}\). Когда компьютер выполняет вычисления, множество проводов внутри него включаются и выключаются по схемам, определяемым определенными правилами. Используемые правила могут быть наиболее естественно выражены в терминах логики. Простое правило может быть таким: «включайте провод \(C\) всякий раз, когда включен провод \(A\) и провод \(B\)». Это правило может быть реализовано аппаратно в виде И ворота . И-затвор представляет собой электронный компонент с двумя входными проводами и одним выходным проводом, чья работа заключается в том, чтобы включать свой выход, когда оба его входа включены, и выключать его выход в любом другом случае. Если мы свяжем «on» с \(\mathbb{T}\) и «off» с \(\mathbb{F}\), и если мы дадим имена \(A\) и \(B\) входы вентиля, то вентиль вычисляет значение логического выражения \(A ∧ B\).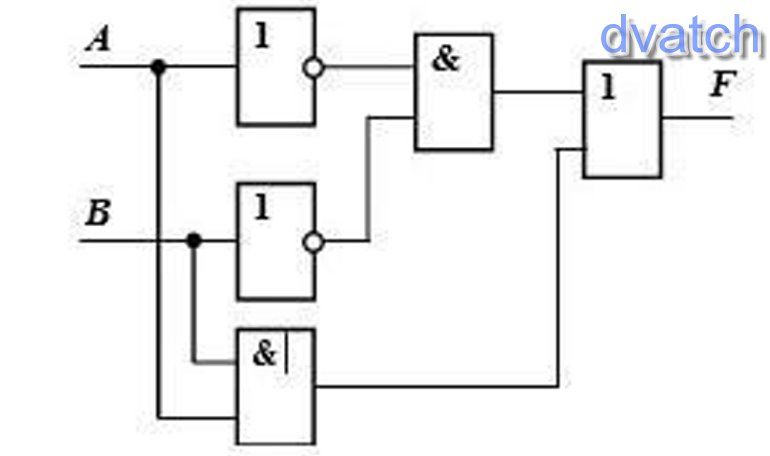 По сути, \(А\) — это предложение со значением «первый вход включен», а \(В\) — это предложение со значением «второй вход включен». Функции вентиля и гарантируют, что выход описывается предложением \(A ∧ B\). То есть выход включен тогда и только тогда, когда включен первый вход и включен второй вход.
По сути, \(А\) — это предложение со значением «первый вход включен», а \(В\) — это предложение со значением «второй вход включен». Функции вентиля и гарантируют, что выход описывается предложением \(A ∧ B\). То есть выход включен тогда и только тогда, когда включен первый вход и включен второй вход.
Элемент ИЛИ представляет собой электронный компонент с двумя входами и одним выходом, который включает свой выход, если один (или оба) из его входов включены. Если входным данным заданы имена \(A\) и \(B\), то логический элемент or вычисляет логическое значение \(A∨B\). Элемент НЕ имеет один вход и один выход, и он выключает свой выход, когда вход включен, и включает, когда вход выключен. Если вход назван \(A\), то вентиль not вычисляет значение \(¬A\).
Возможны, конечно, и другие типы логических вентилей. Ворота можно заставить вычислять, например, \(A → B\) или \(A⊕B\). Однако любое вычисление, которое может быть выполнено с помощью логических элементов, может быть выполнено с использованием только вентилей \(\small{И}\), \(\small{ИЛИ}\) и \(\small{НЕ}\), как мы увидим ниже. (На практике, однако, вентили \(\small{NAND}\) и \(\small{NOR}\), которые вычисляют значения \(¬(A ∧ B)\) и \(¬(A ∨ B)\) соответственно, часто используются, потому что их легче построить из транзисторов, чем вентили \(\small{И} и \(\small{ИЛИ}\).)
(На практике, однако, вентили \(\small{NAND}\) и \(\small{NOR}\), которые вычисляют значения \(¬(A ∧ B)\) и \(¬(A ∨ B)\) соответственно, часто используются, потому что их легче построить из транзисторов, чем вентили \(\small{И} и \(\small{ИЛИ}\).)
Рисунок 1.3: Стандартные символы для трех основных логических вентилей и логическая схема, вычисляющая значение логического выражения (¬A) ∧ (B ∨ ¬(A ∧ C)). Входные провода к каждому логическому элементу находятся слева, а выходной провод справа. Обратите внимание, что когда провода пересекаются друг с другом на схеме, подобной этой, они на самом деле не пересекаются, если только в точке их пересечения нет черного круга.
Три типа логических вентилей представлены стандартными символами, как показано на рис. 1.3. Поскольку входы и выходы логических элементов представляют собой просто провода, несущие сигналы включения/выключения, логические элементы можно соединить вместе, подключив выходы одних элементов к входам других элементов. Результат — логическая схема . Пример также показан на рисунке 1.3.
Результат — логическая схема . Пример также показан на рисунке 1.3.
Логическая схема на рисунке имеет три входа, обозначенных \(A, B,\) и \(C\). Схема вычисляет значение составного предложения \((¬A) ∧ (B ∨ ¬(A ∧C))\). То есть, когда \(A\) представляет предложение «входной провод, помеченный \(A\), включен», и аналогично для \(B\) и \(C\), тогда выход схемы включен, если и только если значение составного предложения \((¬A) ∧ (B ∨ ¬(A ∧ C))\) истинно.
Для любого составного предложения, составленного из операторов \(∧, ∨,\) и \(¬\), можно построить логическую схему, вычисляющую значение этого предложения. Само предложение является планом схемы. Как отмечалось в разделе 1.1, любой логический оператор, с которым мы сталкивались, может быть выражен через \(∧, ∨\) и \(¬\), так что на самом деле каждое составное предложение, которое мы знаем, как написать, может быть вычислено с помощью логическая схема.
Имея предложение, составленное из операторов \(∧, ∨,\) и \(¬\), легко построить схему для его вычисления. Во-первых, определите основной оператор в предложении — тот, значение которого будет вычисляться последним. Рассмотрим \((A ∨B) ∧ ¬(A ∧ B)\). Эта схема имеет два входных значения, \(A\) и \(B\), которые представлены проводами, входящими в схему. Схема имеет выходной провод, который представляет вычисленное значение предложения. Основным оператором в \((A ∨ B) ∧ ¬(A ∧ B)\) является первый оператор \(∧\), который вычисляет значение выражения в целом путем объединения значений подвыражений \(A ∨ B\) и \(¬(A ∧ B)\). Этот оператор \(∧\) соответствует вентилю и в схеме, которая вычисляет конечный результат схемы.
Во-первых, определите основной оператор в предложении — тот, значение которого будет вычисляться последним. Рассмотрим \((A ∨B) ∧ ¬(A ∧ B)\). Эта схема имеет два входных значения, \(A\) и \(B\), которые представлены проводами, входящими в схему. Схема имеет выходной провод, который представляет вычисленное значение предложения. Основным оператором в \((A ∨ B) ∧ ¬(A ∧ B)\) является первый оператор \(∧\), который вычисляет значение выражения в целом путем объединения значений подвыражений \(A ∨ B\) и \(¬(A ∧ B)\). Этот оператор \(∧\) соответствует вентилю и в схеме, которая вычисляет конечный результат схемы.
После того, как основной оператор определен и представлен в виде логического элемента, вам просто нужно построить схемы для вычисления ввода или ввода для этого оператора. В этом примере входы в основную схему и затвор поступают из двух подсхем. Одна подсхема вычисляет значение \(A ∨ B\), а другая вычисляет значение \(¬(A ∧ B)\). Создание каждой подсхемы — это отдельная задача, но меньшая, чем проблема, с которой вы начали.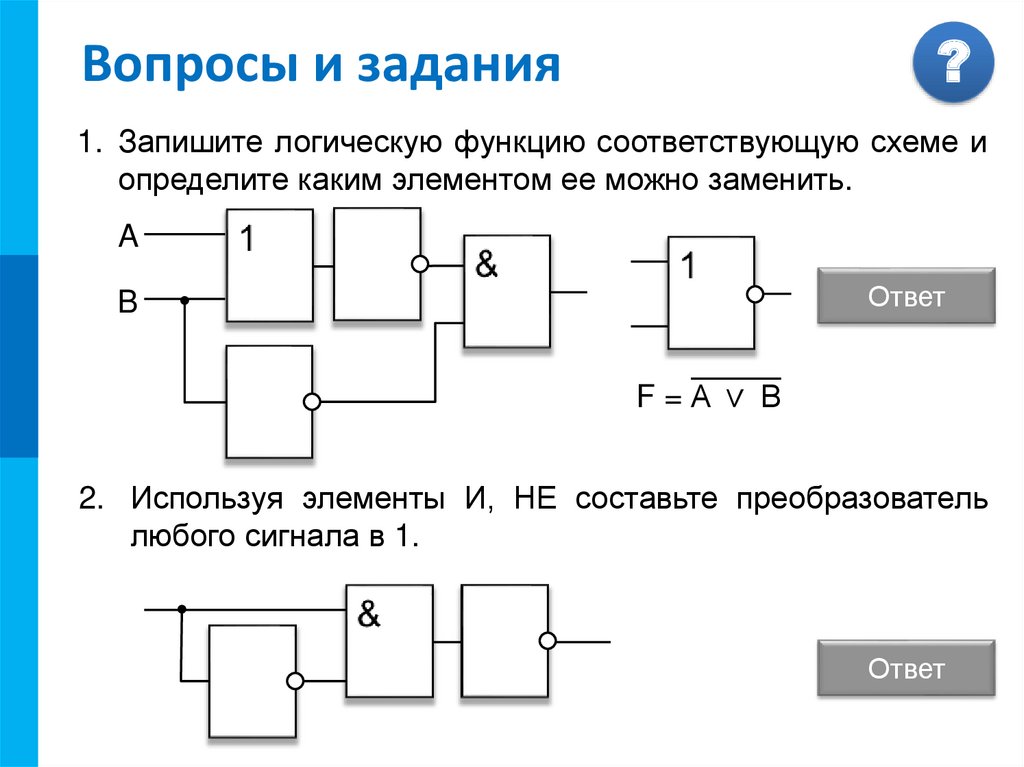 В конце концов, вы придете к вентилю, вход которого поступает непосредственно от одного из входных проводов — в данном случае \(A\) или \(B\), а не от подсхемы.
В конце концов, вы придете к вентилю, вход которого поступает непосредственно от одного из входных проводов — в данном случае \(A\) или \(B\), а не от подсхемы.
Итак, каждое составное предложение вычисляется логической схемой с одним выходным проводом. Верно ли обратное? То есть для данной логической схемы с одним выходом существует ли предложение, выражающее значение выхода через значения входов? Не совсем. Когда вы соединяете несколько логических вентилей в цепь, ничто не мешает вам ввести петли обратной связи. Петля обратной связи возникает, когда выход вентиля соединяется — возможно, через один или несколько промежуточных вентилей — обратно со входом того же вентиля. На рис. 1.5 показан пример схемы с петлей обратной связи. Петли обратной связи не могут быть описаны составными предложениями, в основном потому, что нет места для начала, нет входных данных, которые можно было бы связать с пропозициональной переменной. Но петли обратной связи — единственное, что может пойти не так. Логическая схема, не содержащая контуров обратной связи, называется 9-канальной.0151 комбинаторная логическая схема . Каждая комбинаторная логическая схема только с одним выходом вычисляет значение некоторого составного предложения. Пропозициональные переменные в составном предложении — это просто имена, связанные с входными проводами схемы. (Конечно, если схема имеет более одного выхода, вы можете просто использовать разные предложения для каждого выхода.)
Логическая схема, не содержащая контуров обратной связи, называется 9-канальной.0151 комбинаторная логическая схема . Каждая комбинаторная логическая схема только с одним выходом вычисляет значение некоторого составного предложения. Пропозициональные переменные в составном предложении — это просто имена, связанные с входными проводами схемы. (Конечно, если схема имеет более одного выхода, вы можете просто использовать разные предложения для каждого выхода.)
Ключ к пониманию того, почему это так, заключается в том, чтобы отметить, что каждый провод в цепи, а не только последний выходной провод, представляет значение некоторого предложения. Кроме того, как только вы знаете, какое предложение представлено каждым входным проводом к воротам, становится очевидным, какое предложение представлено выходом: вы просто комбинируете входные предложения с соответствующими \(∧, ∨,\) или \(¬\) привод, в зависимости от типа ворот. Чтобы найти предложение, связанное с конечным выходом, вам просто нужно начать с входов и двигаться по схеме, помечая выходной провод каждого элемента предложением, которое он представляет.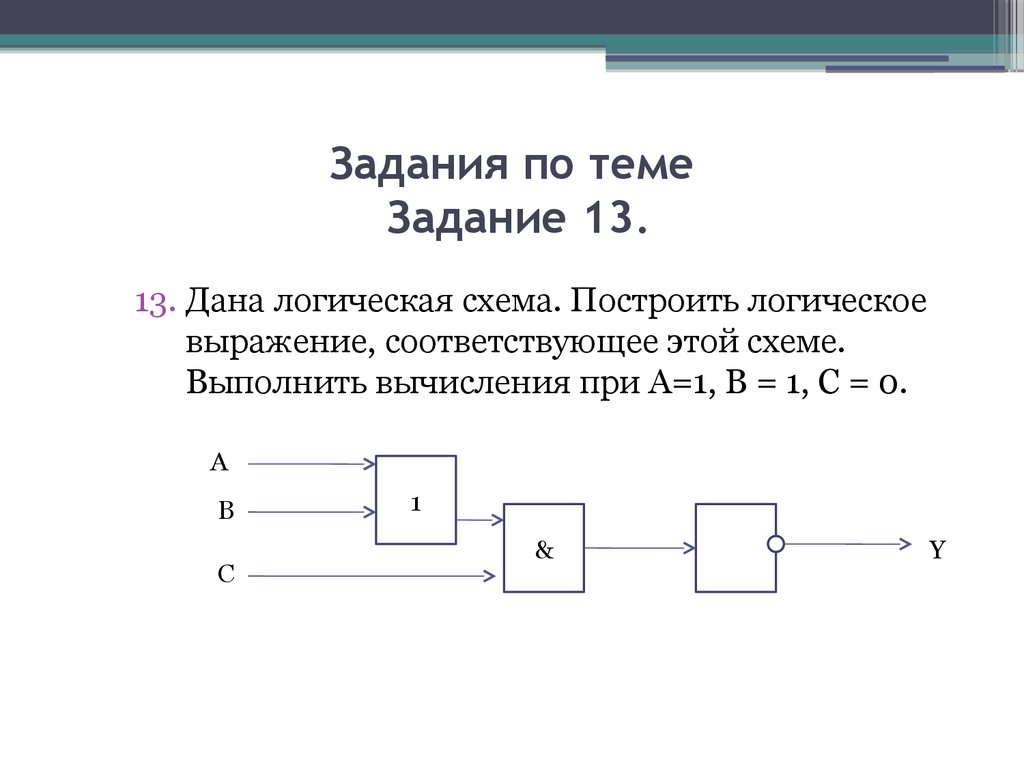 Рисунок 1.6 иллюстрирует этот процесс.
Рисунок 1.6 иллюстрирует этот процесс.
Рисунок 1.4: Этапы построения схемы, вычисляющей составное предложение \((A ∨ B) ∧ ¬(A ∧ B)\).
Таким образом, составные предложения естественным образом соответствуют комбинаторным логическим схемам. Но мы еще не совсем решили вопрос о том, насколько сильны эти контуры и предложения. Мы рассмотрели ряд логических операторов и отметили, что все они могут быть выражены через \(∧, ∨,\) и \(¬\). Но могут ли быть другие операторы, которые нельзя так выразить? Точно так же могут существовать другие типы логических вентилей — возможно, с большим количеством входов, — чьи вычисления нельзя дублировать с помощью \(\small{И}\), \(\small{ИЛИ}\) и \(\small {НЕ}\) ворота? Любой логический оператор или логический вентиль вычисляет значение для каждой возможной комбинации логических значений своих входов. Мы всегда можем составить таблицу истинности, показывающую выходные данные для каждой возможной комбинации входных данных. Оказывается, по любой такой таблице истинности можно найти предложение, содержащее только операторы \(∧, ∨\) и \(¬\), значение которого для каждой комбинации входных данных определяется именно этим стол.
Оказывается, по любой такой таблице истинности можно найти предложение, содержащее только операторы \(∧, ∨\) и \(¬\), значение которого для каждой комбинации входных данных определяется именно этим стол.
Рисунок 1.5: Эта схема содержит контур обратной связи, поэтому она не является комбинаторной логической схемой. Контур обратной связи включает вентиль и и вентиль или справа. Эта схема не вычисляет значение составного предложения. Однако эта схема играет важную роль в памяти компьютера, поскольку ее можно использовать для хранения логического значения.
Чтобы понять, почему это так, полезно ввести особый тип составного предложения. Определите простой термин быть либо пропозициональной переменной, либо отрицанием пропозициональной переменной. Тогда соединение простых терминов будет состоять из одного или нескольких простых терминов, соединенных с операторами ∧. («Союз одного простого термина» — это всего лишь один простой термин сам по себе.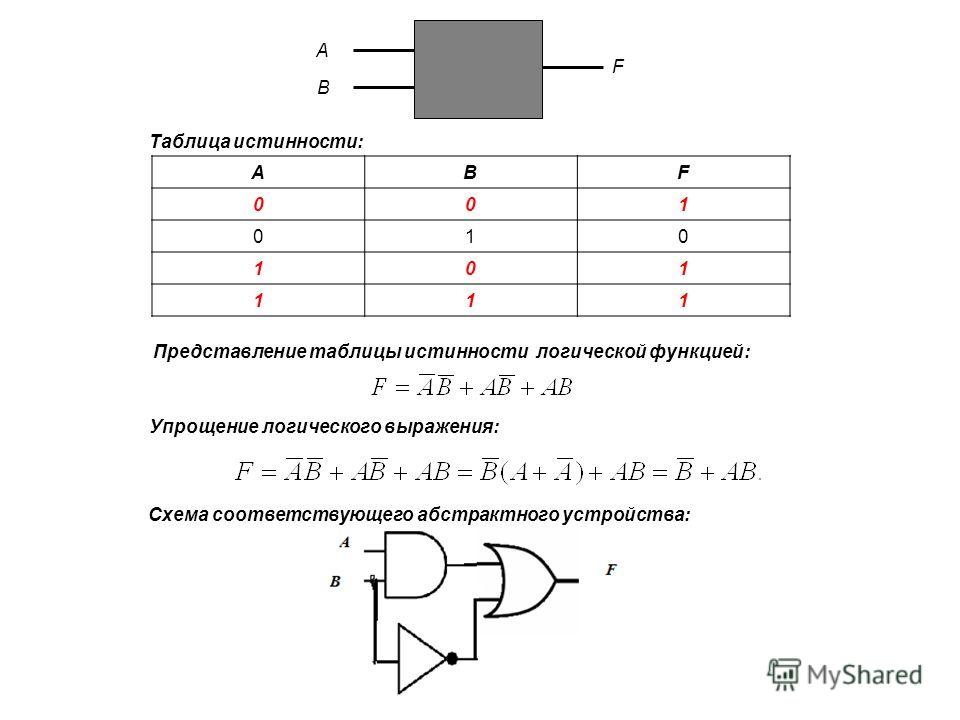 Это может не иметь грамматического смысла, но именно так думают математики.) Некоторыми примерами союзов простых терминов могут быть \(p∧q, p, ¬q\) и \(p∧¬r∧¬w∧s∧t\). Наконец, мы можем взять один или несколько таких союзов и соединить их в «дизъюнкт союзов простых терминов». Это тот тип составного предложения, который нам нужен. Мы можем избежать некоторой избыточности, предположив, что никакая пропозициональная переменная не встречается более одного раза в одной конъюнкции (поскольку \(p∧p\) можно заменить на \(p\), и если \(p\) и \(¬p \) оба встречаются в конъюнкции, то значение конъюнкции ложно, и его можно исключить.) Можно также предположить, что одна и та же конъюнкция не встречается дважды в дизъюнкции.
Это может не иметь грамматического смысла, но именно так думают математики.) Некоторыми примерами союзов простых терминов могут быть \(p∧q, p, ¬q\) и \(p∧¬r∧¬w∧s∧t\). Наконец, мы можем взять один или несколько таких союзов и соединить их в «дизъюнкт союзов простых терминов». Это тот тип составного предложения, который нам нужен. Мы можем избежать некоторой избыточности, предположив, что никакая пропозициональная переменная не встречается более одного раза в одной конъюнкции (поскольку \(p∧p\) можно заменить на \(p\), и если \(p\) и \(¬p \) оба встречаются в конъюнкции, то значение конъюнкции ложно, и его можно исключить.) Можно также предположить, что одна и та же конъюнкция не встречается дважды в дизъюнкции.
Определение 1.5
Говорят, что составное предложение находится в дизъюнктивной нормальной форме или ДНФ, если оно является дизъюнкцией конъюнкций простых терминов и если, кроме того, каждая пропозициональная переменная встречается не более одного раза в каждой конъюнкции и в каждом конъюнкция встречается не более одного раза в дизъюнкции.
Используя \(p, q, r, s, A,\) и \(B\) в качестве пропозициональных переменных, вот несколько примеров пропозиций, которые находятся в дизъюнктивной нормальной форме:
\((p ∧ q ∧ r) ∨ (p ∧ ¬q ∧ r ∧ s) ∨ (¬p ∧ ¬q)\)
\((p∧¬q)\)
\((A∧¬B)∨(¬A∧B)\)
\(p ∨ (¬p ∧ q) ∨ (¬p ∧ ¬q ∧ r) ∨ (¬p ∧ ¬q ∧ ¬r ∧ w)\)
Рисунок 1.6: Поиск предложения, значение которого вычисляется с помощью комбинаторной логической схемы. Каждый провод в цепи помечен предложением, которое он представляет. Нумерация меток показывает один из порядков, в котором они могут быть связаны с проводами. Схема в целом вычисляет значение \(¬(A ∧ B) ∧ (B ∨ ¬C)\).
Предложения в ДНФ — это как раз то, что нам нужно для работы с таблицами ввода-вывода того типа, который мы обсуждали. Любая такая таблица может быть вычислена предложением в дизъюнктивной нормальной форме. Отсюда следует, что можно построить схему для вычисления этой таблицы, используя только вентили \(\small{И}\), \(\small{ИЛИ}\) и \(\small{НЕ}\).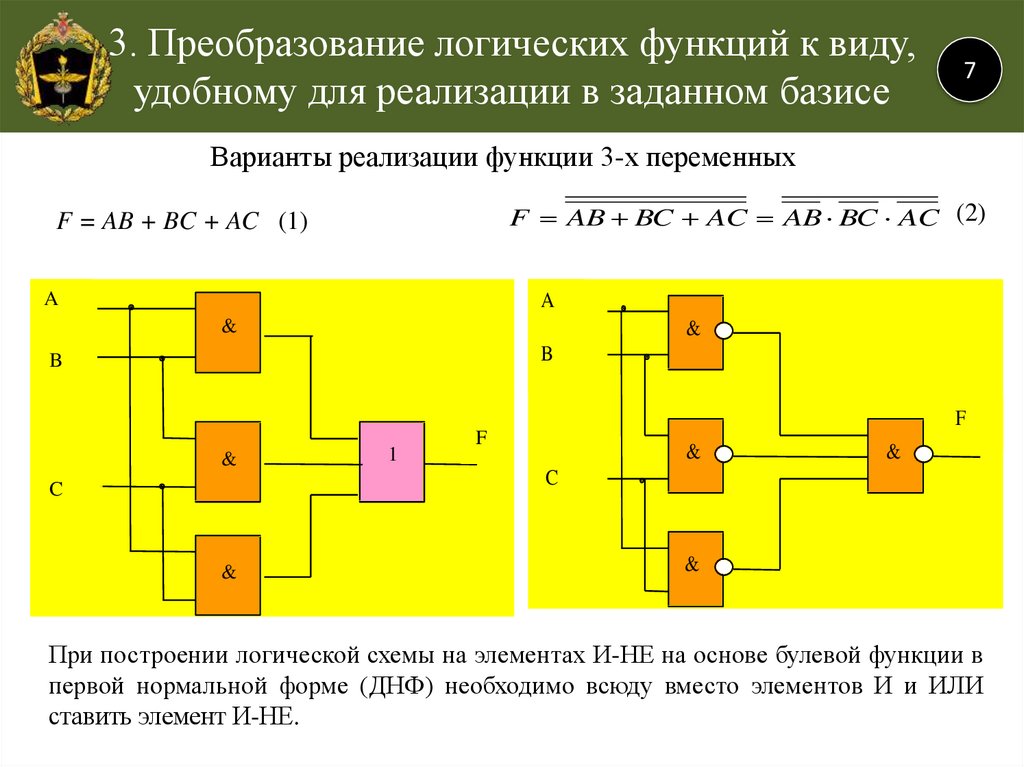
Теорема 1.3
Рассмотрим таблицу, в которой перечислены логические выходные значения для каждой комбинации значений нескольких пропозициональных переменных. Предположим, что хотя бы одно из выходных значений истинно. Тогда существует предложение, содержащее эти переменные, такое, что значение предложения для каждой возможной комбинации значений переменных точно равно значению, указанному в таблице. Предложение можно выбрать в дизъюнктивной нормальной форме.
Доказательство. Рассмотрим любую строку в таблице, для которой выходное значение равно \(\mathbb{T}\). Сформируйте конъюнкцию простых терминов следующим образом: для каждой переменной \(p\), значение которой равно \(mathbb{T}\) в этой строке, включите \(p\) в конъюнкцию; для каждой переменной \(q\), значение которой равно \(mathbb{F}\) в строке, включите \(¬q\) в конъюнкцию. Значение этой конъюнкции равно \(mathbb{T}\) для комбинации значений переменных, заданной в этой строке таблицы, поскольку каждое из условий в конъюнкции истинно для этой комбинации переменных.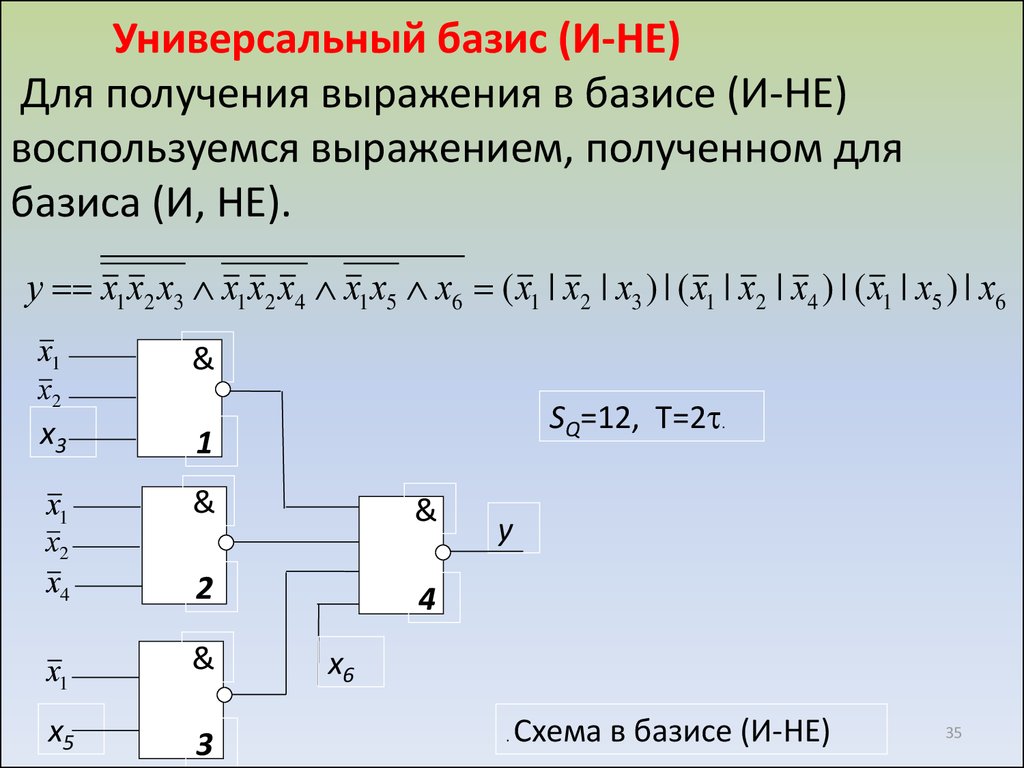 Более того, для любой другой возможной комбинации значений переменных значением конъюнкции будет \(\mathbb{F}\), поскольку по крайней мере одно из простых условий в конъюнкции будет ложным.
Более того, для любой другой возможной комбинации значений переменных значением конъюнкции будет \(\mathbb{F}\), поскольку по крайней мере одно из простых условий в конъюнкции будет ложным.
Возьмем дизъюнкт всех построенных таким образом конъюнкций для каждой строки таблицы, где выходное значение истинно. Эта дизъюнкция имеет значение \(mathbb{T}\) тогда и только тогда, когда одна из составляющих ее конъюнкций имеет значение \(\mathbb{T}\) — и это именно тогда, когда выходное значение, указанное в таблице это \(\mathbb{T}\). Итак, эта дизъюнкция конъюнкций удовлетворяет требованиям теоремы.
В качестве примера рассмотрим таблицу на рис. 1.7. Эта таблица определяет желаемое выходное значение для каждой возможной комбинации значений пропозициональных переменных \(p, q,\) и \(r\). Посмотрите на вторую строку таблицы, где выходное значение истинно. Согласно доказательству теоремы эта строка соответствует конъюнкции \((¬p ∧ ¬q ∧ r)\). Эта конъюнкция истинна, когда \(p\) ложно, \(q\) ложно и \(r\) истинно; во всех остальных случаях оно ложно, так как в любом другом случае хотя бы одно из слагаемых \(¬p, ¬q\) или \(r\) ложно. Две другие строки, в которых результат верен, дают еще две конъюнкции. Три соединения объединяются, чтобы получить предложение ДНФ \((¬p∧¬q∧r)∨(¬p∧q∧r)∨(p∧q∧r)\). Это предложение вычисляет все выходные значения, указанные в таблице. Используя это предложение в качестве схемы, мы получаем логическую схему, выходы которой соответствуют указанным в таблице.
Две другие строки, в которых результат верен, дают еще две конъюнкции. Три соединения объединяются, чтобы получить предложение ДНФ \((¬p∧¬q∧r)∨(¬p∧q∧r)∨(p∧q∧r)\). Это предложение вычисляет все выходные значения, указанные в таблице. Используя это предложение в качестве схемы, мы получаем логическую схему, выходы которой соответствуют указанным в таблице.
Теперь для любой комбинаторной логической схемы существует множество других схем, которые имеют такое же поведение ввода/вывода. Когда две схемы имеют одну и ту же таблицу ввода/вывода, составные предложения, связанные с двумя схемами, логически эквивалентны. Иными словами, предложения, которые логически эквивалентны, создают схемы с одинаковым входным/выходным поведением. С практической точки зрения мы обычно предпочитаем более простую схему. Соответствие между схемами и предложениями позволяет нам применять булеву алгебру к упрощению схем.
Например, рассмотрим предложение ДНФ, соответствующее таблице на рис. 1.7. В \((¬p∧¬q∧r)∨(¬p∧q∧r)∨(p∧q∧r)\) мы можем разложить \((q∧r)\) из двух последних членов, что дает \((¬p∧¬q∧r)∨((¬p∨p)∧(q∧r))\).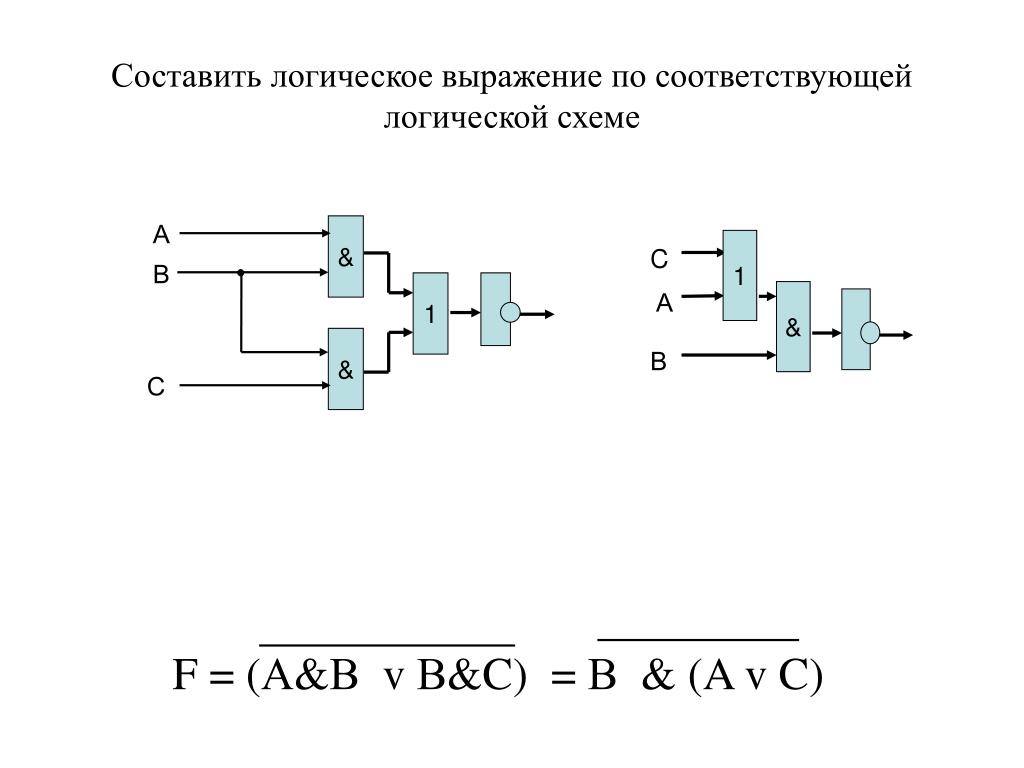 8\) 98\small{Нет, я не ошибся. В исходном выражении есть одиннадцать логических операторов, но вы можете обойтись десятью вентилями в схеме: используйте один вентиль not для вычисления ¬p и соедините выход этого вентиля с двумя разными вентилями и. Повторное использование вывода логического элемента — очевидный способ упростить схемы, которые не соответствуют ни одной операции над предложениями.}\)
8\) 98\small{Нет, я не ошибся. В исходном выражении есть одиннадцать логических операторов, но вы можете обойтись десятью вентилями в схеме: используйте один вентиль not для вычисления ¬p и соедините выход этого вентиля с двумя разными вентилями и. Повторное использование вывода логического элемента — очевидный способ упростить схемы, которые не соответствуют ни одной операции над предложениями.}\)
Рисунок 1.7: Таблица ввода/вывода, определяющая желаемый результат для каждой комбинации значений пропозициональных переменных p, q и r. Каждая строка, в которой выходом является T, соответствует конъюнкции, показанной рядом с этой строкой в таблице. Дизъюнкция этих союзов есть высказывание, выходные значения которого в точности совпадают с указанными в таблице.
Если вы начинаете со схемы вместо предложения, часто можно найти связанное предложение, упростить его с помощью булевой алгебры и использовать упрощенное предложение для построения эквивалентной схемы, которая проще исходной.
Все это прекрасно объясняет взаимосвязь между логикой и схемами, но не объясняет, почему именно логические схемы должны использоваться в компьютерах. Часть объяснения заключается в том, что компьютеры используют двоичные числа. Двоичное число представляет собой строку из нулей и единиц. Двоичные числа легко представить в электронном устройстве, таком как компьютер: каждая позиция в числе соответствует проводу. Когда провод включен, он представляет единицу; когда провод выключен, он представляет ноль. Когда мы думаем с точки зрения логики, одни и те же состояния провода представляют истинное и ложное, но любое представление — это просто интерпретация реальности, которая представляет собой провод, который может быть включен или выключен. Вопрос в том, плодотворна ли интерпретация.
Когда провода представляют собой нули и единицы, мы можем создавать схемы для выполнения вычислений с двоичными числами. Какие вычисления?
Рисунок 1.8: Таблицы ввода/вывода для сложения трех двоичных цифр, \(A, B,\) и \(C\).
Все, что захотим! Если мы знаем, каким должен быть ответ для каждой комбинации входных данных, то по теореме 1.3 мы можем построить схему для вычисления этого ответа. Конечно, процедура, описанная в этой теореме, применима только для небольших схем, но маленькие схемы можно использовать в качестве строительных блоков для создания всех вычислительных схем в компьютере.
Например, давайте посмотрим на двоичное сложение. Чтобы сложить два обычных десятичных числа, вы выстраиваете их одно над другим и добавляете цифры в каждом столбце. В каждом столбце также может быть перенос из предыдущего столбца. Чтобы сложить столбец, вам нужно запомнить лишь небольшое количество правил, таких как \(7+6+1 = 14\) и \(3+5+0 = 8\). Для двоичного сложения еще проще, так как единственные цифры 0 и 1. Правил всего восемь:
\(0 + 0 + 0 = 00\) \(0 + 0 + 1 = 01\) \(0 + 1 + 0 = 01\) \(0 + 1 + 1 = 10\) | \(1 + 0 + 0 = 01\) \(1 + 0 + 1 = 10\) \(1 + 1 + 0 = 10\) \(1 + 1 + 1 = 11\) |
Здесь я записал каждую сумму двумя цифрами.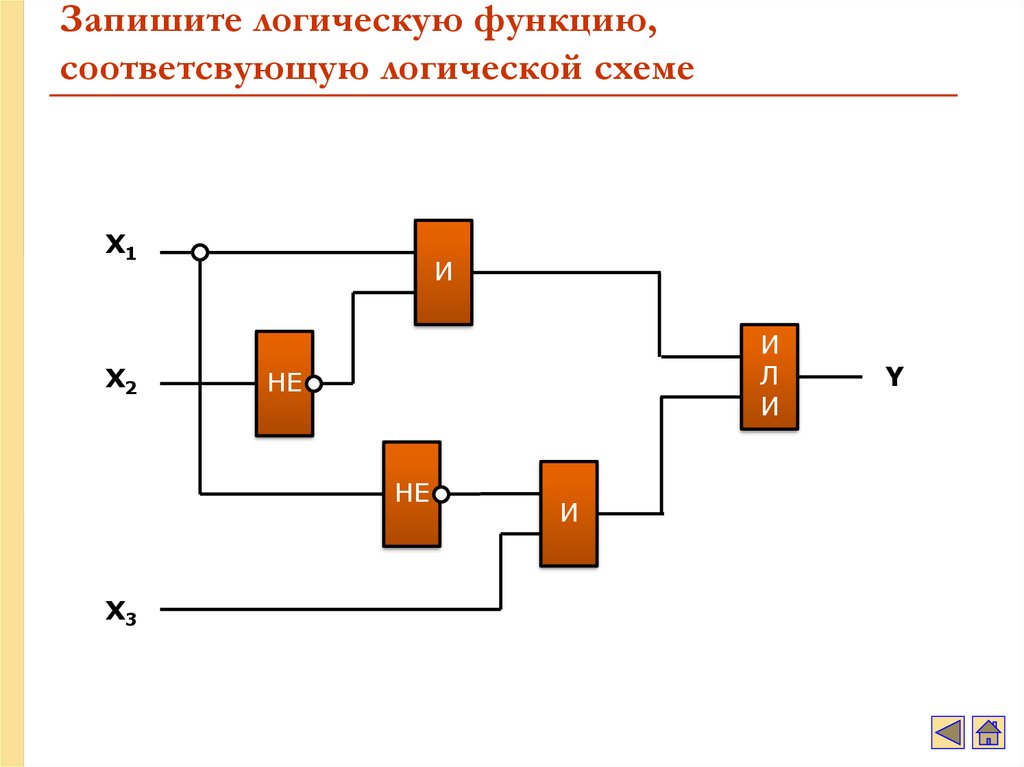 При сложении нескольких столбцов одна из этих цифр переносится в следующий столбец. Здесь у нас есть расчет, который имеет три входа и два выхода. Мы можем сделать таблицу ввода/вывода для каждого из двух выходов. Таблицы показаны на рисунке 1.8. Мы знаем, что эти таблицы могут быть реализованы в виде комбинаторных схем, поэтому мы знаем, что схемы могут складывать двоичные числа. Чтобы складывать многоразрядные двоичные числа, нам просто нужна одна копия базовой схемы сложения для каждого столбца в сумме.
При сложении нескольких столбцов одна из этих цифр переносится в следующий столбец. Здесь у нас есть расчет, который имеет три входа и два выхода. Мы можем сделать таблицу ввода/вывода для каждого из двух выходов. Таблицы показаны на рисунке 1.8. Мы знаем, что эти таблицы могут быть реализованы в виде комбинаторных схем, поэтому мы знаем, что схемы могут складывать двоичные числа. Чтобы складывать многоразрядные двоичные числа, нам просто нужна одна копия базовой схемы сложения для каждого столбца в сумме.
Эта страница под названием 1.3: Application — Logic Circuits распространяется под лицензией CC BY-NC-SA, авторами, ремиксами и/или кураторами являются Кэрол Кричлоу и Дэвид Дж. Эк.

 Этот метод не работает, если вы попытаетесь применить его к схеме, содержащей петлю обратной связи. Что пойдет не так? Приведите пример.
Этот метод не работает, если вы попытаетесь применить его к схеме, содержащей петлю обратной связи. Что пойдет не так? Приведите пример.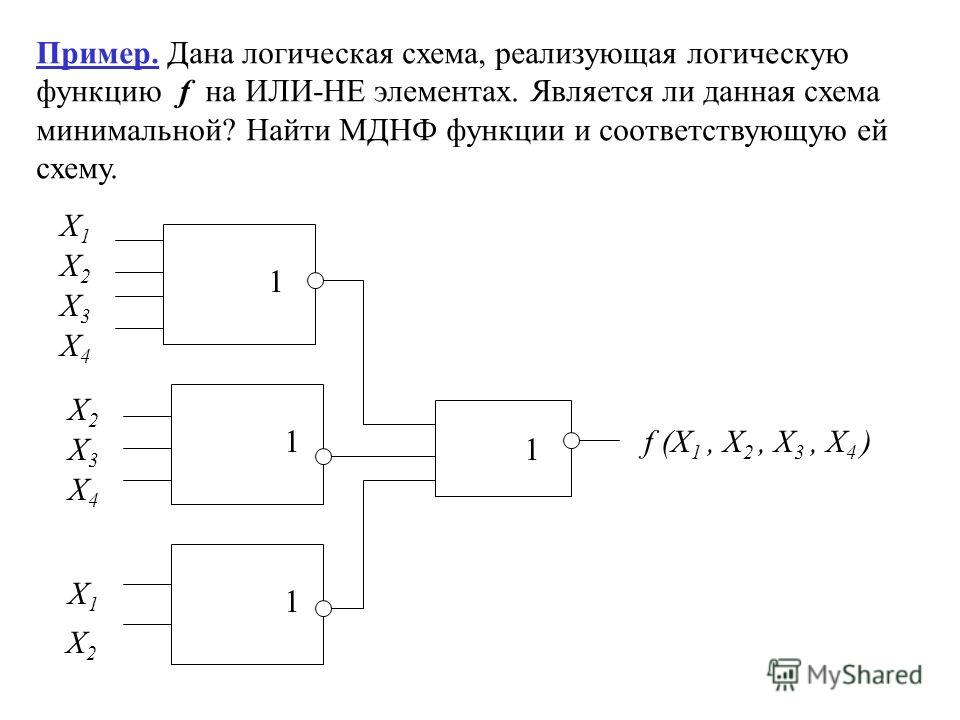 Покажите, что каждое сложное предложение, не являющееся тавтологией, логически эквивалентно сложному предложению в конъюнктивной нормальной форме. (Подсказка: что произойдет, если вы возьмете отрицание предложения ДНФ и примените законы ДеМоргана?)
Покажите, что каждое сложное предложение, не являющееся тавтологией, логически эквивалентно сложному предложению в конъюнктивной нормальной форме. (Подсказка: что произойдет, если вы возьмете отрицание предложения ДНФ и примените законы ДеМоргана?)
Leave A Comment