Графики зависимости кинематических величин от времени при равномерном и равноускоренном движении
Цели урока:
обучающая: рассмотреть и сформировать навыки построения графиков зависимости кинематических величин от времени при равномерном и равноускоренном движении; научить учащихся анализировать эти графики; путем решения задач закрепить полученные знания на практике;
развивающая: развитие умения наблюдать, анализировать конкретные ситуации; выделять определенные признаки;
воспитывающая: воспитание дисциплины и норм поведения, творческого отношения к изучаемому предмету; стимулировать активность учащихся.
Методы:
словесный — беседа;
наглядный — видеоурок, записи на доске;
контролирующий — тестирование или устный (письменный) опрос, решение задач).
Связи:
межпредметные: математика — линейная зависимость, график линейной функции; квадратичная функция и ее график;
внутрипредметные: равномерное и равноускоренное движение.
Ход урока:
1. Организационный этап.
Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.
2. Актуализация знаний.
3. Объяснение нового материала.
Мы с вами знаем, что механическое движение — это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.
В свою очередь механическое движение бывает двух видов — равномерное, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, и неравномерным, при котором тело за любые равные промежутки времени совершает разные перемещения.
Давайте вспомним основные формулы, которые мы выучили для равномерного и неравномерного движения.
Если движение равномерное, то:
1. Скорость тела не меняется с течением времени;
Скорость тела не меняется с течением времени;
2. Что бы найти скорость тела, необходимо путь, который прошло тело за некоторый промежуток времени, разделить на этот промежуток времени;
3. Уравнение перемещения имеет вид:
4. И — кинематическое уравнение равномерного движения.
Для равноускоренного:
1. Ускорение тела не изменяется с течением времени;
2. Ускорение есть величина, равная отношению изменения скорости тела, к промежутку времени, в течении которого это изменение произошло
3. Уравнение скорости для равноускоренного движения имеет вид:
4. — уравнение перемещения для равноускоренного движения;
5. — кинематическое уравнение равноускоренного движения.
Для большей наглядности движение можно описывать с помощью графиков.
Рассмотрим зависимость ускорения, которым может обладать тело вследствие своего движения, от времени.
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения ускорения тела, полученный график будет выражать зависимость ускорения тела от времени.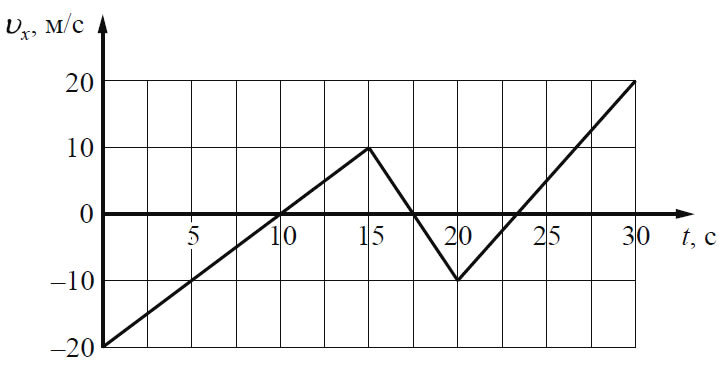
Для равномерного прямолинейного движения график зависимости ускорения от времени имеет вид прямой, которая совпадает с осью времени, т.к. ускорение при равномерном движении равно нулю.
Для равноускоренного движения график ускорения также имеет вид прямой, параллельной оси времени. При этом график располагается над осью времени, если тело движется ускоренно, и под осью времени, если тело движется замедленно.
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, а по вертикальной оси ординат — тоже в соответствующем масштабе — значения скорости тела, то мы получим график скорости.
Для равномерного движения график скорости имеет вид прямой, параллельной оси времени. При этом график скорости располагается над осью времени, если тело движется по оси Х, и под осью времени, если тело движется против оси Х.
Такие графики показывают, как изменяется скорость с течением времени, т. е. как скорость зависит от времени. В случае прямолинейного равномерного движения эта «зависимость» состоит в том, что скорость с течением времени не меняется.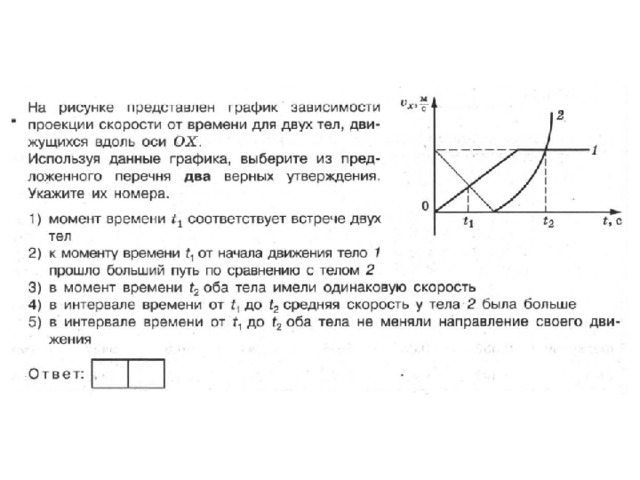 Поэтому график скорости представляет собой прямую, параллельную оси времени.
Поэтому график скорости представляет собой прямую, параллельную оси времени.
По графику скорости тоже можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованного прямоугольника: верхнего, если тело движется в сторону положительного направления, и нижнего — в случае движения тела в отрицательном направлении.
Действительно, площадь прямоугольника равна произведению его сторон: S=ab, где a и b стороны прямоугольника.
Но одна из сторон в определенном масштабе равна времени, а другая — скорости. А их произведение как раз и равно абсолютному значению перемещения тела. При этом перемещение будет положительным, если проекция вектора скорости положительна, и отрицательным, если проекция вектора скорости отрицательна.
При равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле v = v0 + at, т.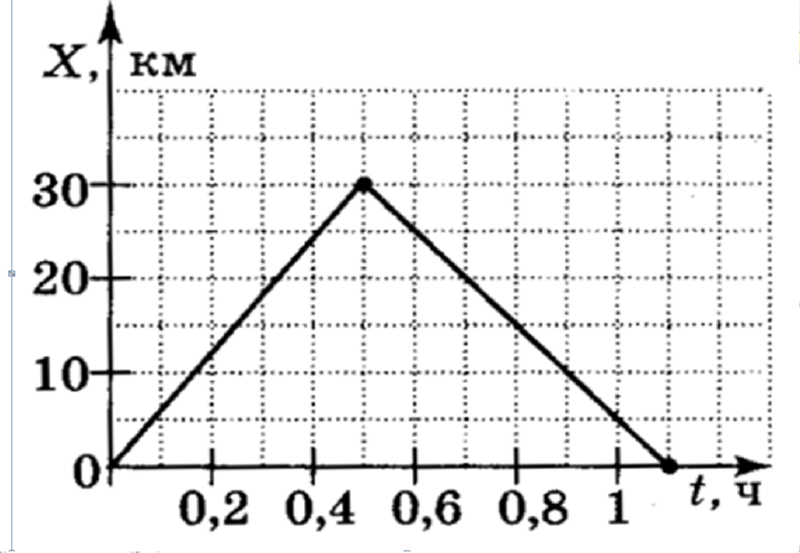 е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой, наклоненную к оси времени. Причем, чем больше угол наклона, те большую скорость имеет тело. На нашем графике прямая 1 соответствует движению с положительным ускорением (скорость увеличивается) и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением (скорость убывает) и начальной скоростью равной нулю.
е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой, наклоненную к оси времени. Причем, чем больше угол наклона, те большую скорость имеет тело. На нашем графике прямая 1 соответствует движению с положительным ускорением (скорость увеличивается) и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением (скорость убывает) и начальной скоростью равной нулю.
По графику скорости при равноускоренном движении также можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованной трапеции для тела 1, и прямоугольного треугольника — в противоположном случае. Действительно, например, площадь трапеции равна произведению полу суммы её оснований на высоту. В нашем случае, в определенном масштабе, высота трапеции равна времени, а основания — начальной и конечной скорости.
При этом проекция перемещения для первого тела будет положительной.
Для второго тела, прямоугольного треугольника — половине произведения его катетов. В нашем случае, катеты — это время и конечная скорость тела.
В нашем случае, катеты — это время и конечная скорость тела.
Проекция перемещения — отрицательна.
Теперь рассмотрим зависимость пройденного пути от времени.
Как и в предыдущих случаях, по оси абсцисс мы будем откладывать время, с момента начала движения, а по оси ординат — путь.
Для равномерного движения график зависимости пути от времени представляет собой прямую линию, т.к. зависимость — линейная.
При этом наклон графика к оси времени зависит от модуля скорости: чем больше скорость, тем больший угол наклона и тем больше скорость движения тела.
При равноускоренном движении графиком будет являться ветка параболы, т.к. зависимость, в этом случае, будет квадратичной. И чем больше ускорение, с которым движется тело, тем сильнее график будет прижиматься к оси ординат.
Теперь перейдем к рассмотрению зависимости перемещения от времени.
Рассмотрим равномерное движение.
Т.к. при равномерном движении перемещение линейно зависит от времени (sx = υxt), то графиком будет являться прямая линия.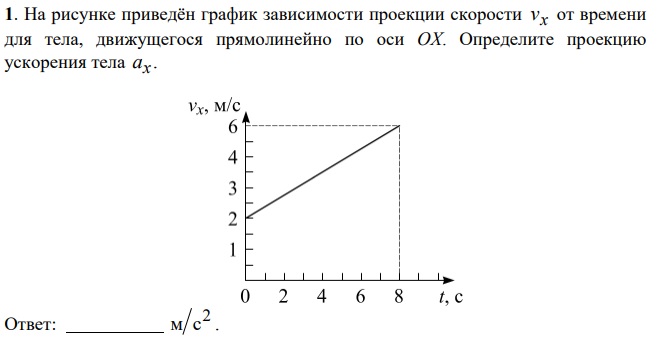 Направление и угол наклона графика к оси времени будет зависеть от проекции вектора скорости на координатную ось.
Направление и угол наклона графика к оси времени будет зависеть от проекции вектора скорости на координатную ось.
Так, в нашем случае, тела 2 и 3 движутся в положительном направлении оси Х, при этом скорость третьего тела больше скорости второго.
А тело 1 — в направлении, противоположном направлению оси Х, поэтому график располагается под осью времени.
Для равноускоренного движения графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения.
Для 1-го тела ускорение меньше нуля, начальная скорость равна нулю.
Для 2-го тела ускорение и начальная скорость тела больше нуля.
Для 3-го тела ускорение больше нуля, начальная скорость меньше нуля.
У 4-го тела начальная скорость и ускорение меньше нуля.
Для 5-го тела ускорение больше нуля, а начальная скорость равна нулю.
И, наконец, 6-ое тело двигается замедленно, но с некоторой начальной скоростью.
И последнее, что мы с вами рассмотрим — это зависимость координаты тела от времени.
Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения координаты тела, полученный график будет выражать зависимость координаты тела от времени (его также называют графиком движения).
Для равноускоренного движения графиком движения, как и в случае перемещения, является парабола, положение вершины которой также зависит от направлений начальной скорости и ускорения.
График равномерного движения представляет собой прямую линию. Это значит, что координата линейно зависит от времени.
В случае прямолинейного движения тела графики движения дают полное решение задачи механики, так как они позволяют найти положение тела в любой момент времени, в том числе и в моменты времени, предшествовавшие начальному моменту (если предположить, что тело двигалось с такой же скоростью и до начала отсчета времени).
С помощью графика движения можно определить:
1.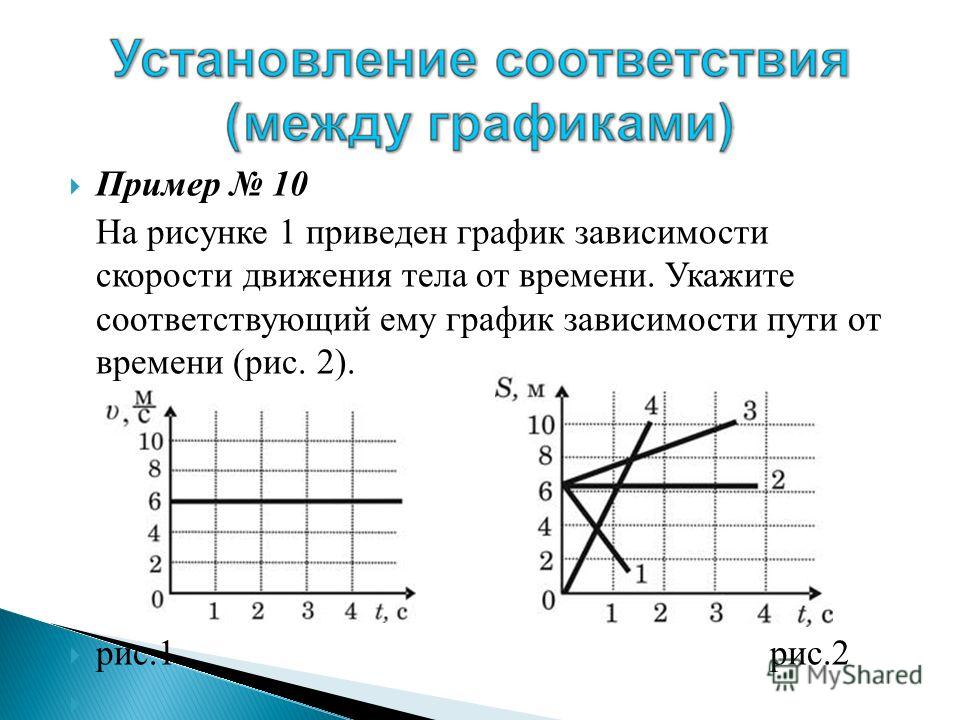 координаты тела в любой момент времени;
координаты тела в любой момент времени;
2. путь, пройденный телом за некоторый промежуток времени;
3. время, за которое пройден какой-то путь;
4. кратчайшее расстояние м/у телами в любой момент времени;
5. момент и место встречи и т. д.
По виду графиков зависимости координаты от времени можно судить и о скорости движения. Ясно, что скорость тем больше, чем круче график, т. е. чем больше угол между ним и осью времени (чем больше этот угол, тем больше изменение координаты за одно и то же время).
При этом надо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.
4. Этап обобщения и закрепления нового материала
И так, сделаем главный вывод.
Механическое движение для большей наглядности можно описывать с помощью графиков:
1) Зависимости скорости от времени;
2) Зависимости ускорения от времени;
3) Зависимость координаты тела от времени;
4) И зависимости перемещения тела от времени, в течении которого это перемещение произошло.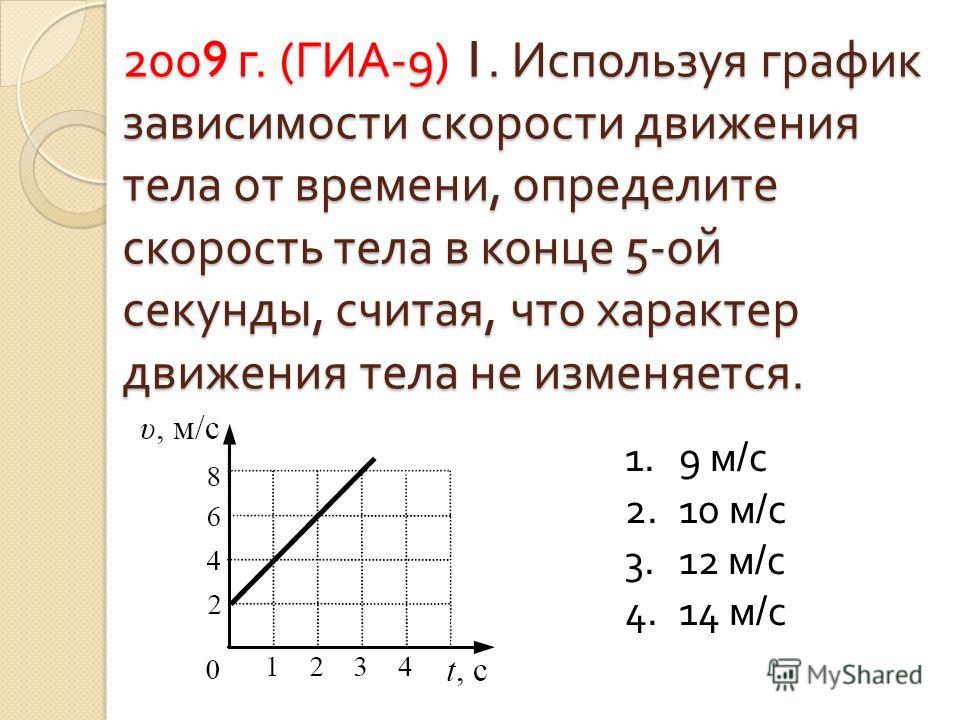
5. Рефлексия
Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.
6. Домашнее задание.
3.6 Определение скорости и смещения по ускорению
Цели обучения
К концу этого раздела вы сможете:
- Выводить кинематические уравнения для постоянного ускорения с помощью интегрального исчисления.
- Использовать интегральную формулировку кинематических уравнений при анализе движения.
- Найдите функциональную форму зависимости скорости от времени по заданной функции ускорения.
- Найдите функциональную форму зависимости положения от времени по заданной функции скорости.
В этом разделе предполагается, что у вас достаточно знаний в области исчисления, чтобы быть знакомым с интеграцией. В разделах «Мгновенная скорость и скорость» и «Среднее и мгновенное ускорение» мы ввели кинематические функции скорости и ускорения с помощью производной. Взяв производную от функции положения, мы нашли функцию скорости, и точно так же, взяв производную от функции скорости, мы нашли функцию ускорения. Используя интегральное исчисление, мы можем работать в обратном направлении и вычислять функцию скорости из функции ускорения, а функцию положения из функции скорости.
Взяв производную от функции положения, мы нашли функцию скорости, и точно так же, взяв производную от функции скорости, мы нашли функцию ускорения. Используя интегральное исчисление, мы можем работать в обратном направлении и вычислять функцию скорости из функции ускорения, а функцию положения из функции скорости.
Кинематические уравнения интегрального исчисления
Начнем с частицы с ускорением a (t) — известная функция времени. Поскольку производная по времени от функции скорости есть ускорение,
[латекс] \фрак{д}{дт}в(т)=а(т), [/латекс]
, мы можем взять неопределенный интеграл от обеих сторон, нахождение
[латекс] \int \frac{d}{dt}v(t)dt=\int a(t)dt+{C}_{1}, [/latex]
где C 1 есть постоянная интегрирования. Поскольку [латекс] \int \frac{d}{dt}v(t)dt=v(t) [/latex], скорость определяется как
[латекс] v(t)=\int a(t)dt+{C}_{1}. [/latex]
Точно так же производная по времени от функции положения является функцией скорости,
[latex] \frac{d}{dt}x(t)=v(t). [/latex]
[/latex]
Таким образом, мы можем использовать те же математические манипуляции, которые мы только что использовали, и найти
[latex] x(t)=\int v(t)dt+{C}_{2}, [/latex]
где C 2 — вторая постоянная интегрирования.
Используя эти интегралы, мы можем вывести кинематические уравнения для постоянного ускорения. С a ( t ) = a константа, и, выполняя интегрирование на (рис.), мы находим
[латекс] v(t)=\int adt+{C}_{1}=at+{C }_{1}. [/latex]
Если начальная скорость равна v (0) = v 0 , тогда
[латекс] {v}_{0}=0+{C}_{1}. [/latex]
Тогда C 1 = v 0 и
[латекс] v(t)={v}_{0}+at, [/latex]
, что (Уравнение). Подстановка этого выражения в (Рисунок) дает 9{2} [/латекс]. а) Какова функция скорости моторной лодки? б) В какой момент времени скорость достигает нуля? в) Какова функция положения моторной лодки? г) Каково водоизмещение моторной лодки с момента начала торможения до момента, когда скорость равна нулю? (e) Нарисуйте график функций скорости и положения.
Стратегия
(a) Чтобы получить функцию скорости, мы должны проинтегрировать и использовать начальные условия, чтобы найти константу интегрирования. (b) Приравняем функцию скорости к нулю и решим для т . (c) Точно так же мы должны проинтегрировать, чтобы найти функцию положения, и использовать начальные условия, чтобы найти константу интегрирования. (d) Поскольку начальная позиция принимается равной нулю, нам нужно только оценить функцию позиции в [латекс] t=0 [/латекс].
Решение
Примем t = 0 за время, когда лодка начинает замедляться.
- Из функциональной формы ускорения мы можем решить (Рисунок), чтобы получить v ( t ):
Показать ответ
Показать ответ
- Решите (Рисунок):
Показать ответ
Показать ответ
Рис.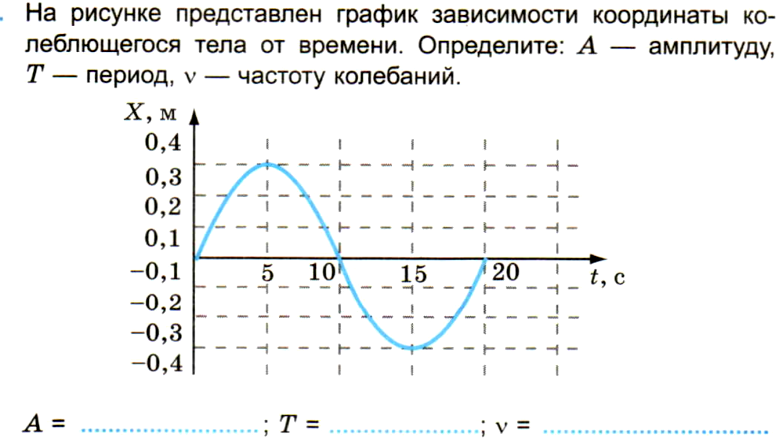
Значение
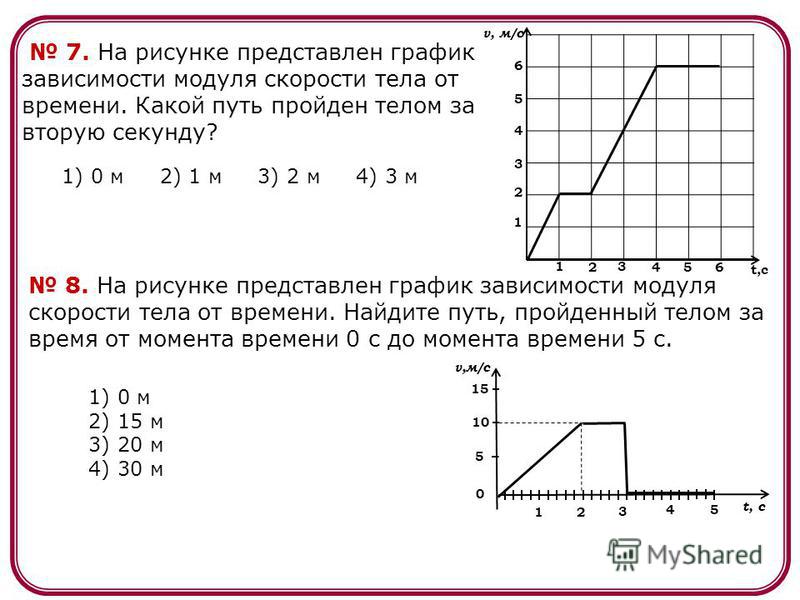 {2} [/латекс]. а) Что такое функция скорости? б) Что такое функция положения? в) Когда скорость равна нулю?
{2} [/латекс]. а) Что такое функция скорости? б) Что такое функция положения? в) Когда скорость равна нулю?Показать решение
Резюме
- Интегральное исчисление дает нам более полную формулировку кинематики.
- Если известно ускорение a ( t ), мы можем использовать интегральное исчисление для получения выражений для скорости v ( t ) и положения x ( t ).
- Если ускорение постоянно, интегральные уравнения сводятся к (Рисунок) и (Рисунок) для движения с постоянным ускорением.
Ключевые уравнения
Концептуальные вопросы
Какая дополнительная информация необходима для определения функции скорости и функции положения при наличии функции ускорения?
Задачи
Ускорение частицы изменяется со временем согласно уравнению [латекс] a(t)=p{t}^{2}-q{t}^{3} [/latex]. Первоначально скорость и положение равны нулю. а) Как зависит скорость от времени? б) Что такое положение как функция времени? 9{1\,\text{/}2} [/latex], где A и B — константы. (a) Если x в метрах, а t в секундах, каковы единицы A и B ? (b) Если ракета стартует из состояния покоя, как изменится скорость между t = 0 и t = t 0 ? в) Если ее начальное положение равно нулю, каково положение ракеты в зависимости от времени в течение этого же интервала времени?
Первоначально скорость и положение равны нулю. а) Как зависит скорость от времени? б) Что такое положение как функция времени? 9{1\,\text{/}2} [/latex], где A и B — константы. (a) Если x в метрах, а t в секундах, каковы единицы A и B ? (b) Если ракета стартует из состояния покоя, как изменится скорость между t = 0 и t = t 0 ? в) Если ее начальное положение равно нулю, каково положение ракеты в зависимости от времени в течение этого же интервала времени?
Показать решение 9{-1} [/латекс], где A = 2 м/с, B = 0,25 м и [латекс] 1,0\,\text{s}\le t\le 8,0\,\text{s } [/латекс]. Определить ускорение и положение частицы при t = 2,0 с и t = 5,0 с. Предположим, что [латекс] x(t=1\,\text{s})=0 [/латекс].
Частица, находящаяся в состоянии покоя, покидает начало координат, и ее скорость увеличивается со временем согласно формуле v ( t ) = 3,2 t м/с.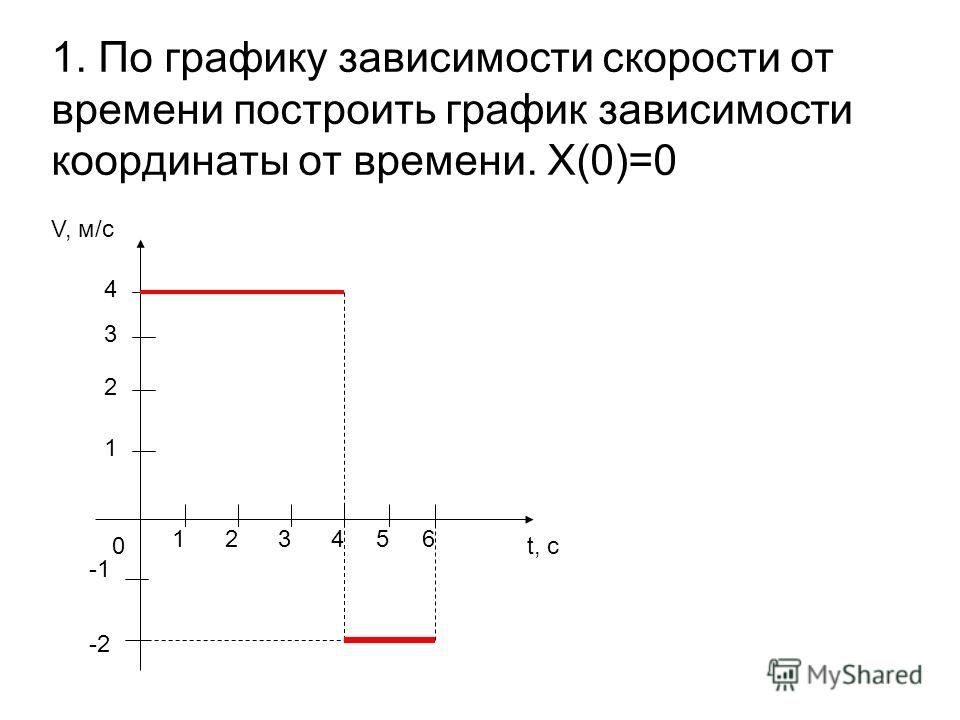 Через 5,0 с скорость частицы начинает уменьшаться согласно [16,0 – 1,5( t – 5,0)] м/с. Это уменьшение продолжается до t = 11,0 с, после чего скорость частицы остается постоянной и равной 7,0 м/с. а) Как зависит ускорение частицы от времени? б) Каково положение частицы на t = 2,0 с, t = 7,0 с и t = 12,0 с?
Через 5,0 с скорость частицы начинает уменьшаться согласно [16,0 – 1,5( t – 5,0)] м/с. Это уменьшение продолжается до t = 11,0 с, после чего скорость частицы остается постоянной и равной 7,0 м/с. а) Как зависит ускорение частицы от времени? б) Каково положение частицы на t = 2,0 с, t = 7,0 с и t = 12,0 с?
Показать решение
Дополнительные задачи
Профессиональный игрок в бейсбол Нолан Райан мог подать бейсбольный мяч со скоростью примерно 160,0 км/ч. При такой средней скорости сколько времени потребовалось мячу, брошенному Райаном, чтобы достичь домашней площадки, которая находится в 18,4 м от насыпи питчера? Сравните это со средним временем реакции человека на зрительный стимул, которое составляет 0,25 с.
Самолет вылетает из Чикаго и совершает 3000-километровый перелет в Лос-Анджелес за 5 часов. Второй самолет вылетает из Чикаго на полчаса позже и прибывает в Лос-Анджелес в то же время. Сравните средние скорости двух самолетов. Не обращайте внимания на кривизну Земли и разницу в высоте между двумя городами.
Сравните средние скорости двух самолетов. Не обращайте внимания на кривизну Земли и разницу в высоте между двумя городами.
Показать решение
Необоснованные результаты Велосипедист проезжает 16,0 км на восток, затем 8,0 км на запад, затем 8,0 км на восток, затем 32,0 км на запад и, наконец, 11,2 км на восток. Если его средняя скорость равна 24 км/ч, то за какое время он проделал путь? Это разумный срок? 9{2} [/латекс] м. Каковы скорость и ускорение при [латексе] t=2,0 [/латекс] с и [латекс] t=5,0 [/латекс] с?
Частица, движущаяся с постоянным ускорением, имеет скорости [латекс] 2,0\,\text{м/с} [/латекс] при [латекс] t=2,0 [/латекс] с и [латекс] -7,6\,\текст {м/с} [/латекс] при [латекс] t=5,2 [/латекс] с. Чему равно ускорение частицы?
Показать решение
Поезд движется вверх по крутому склону с постоянной скоростью (см. следующий рисунок), когда его камбуз отрывается и начинает свободно катиться по рельсам.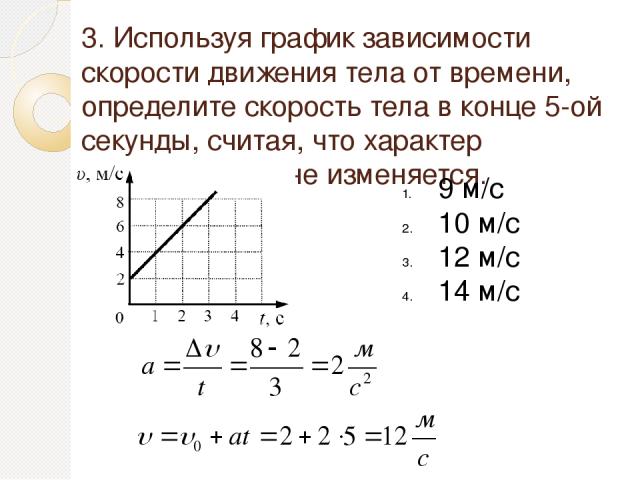 Через 5,0 с камбуз отстает от поезда на 30 м. Каково ускорение камбуза? 9{2} [/latex] по той же прямой. а) Какова скорость электрона, когда он вылетает из этой области? б) Сколько времени требуется электрону, чтобы пересечь область?
Через 5,0 с камбуз отстает от поезда на 30 м. Каково ускорение камбуза? 9{2} [/latex] по той же прямой. а) Какова скорость электрона, когда он вылетает из этой области? б) Сколько времени требуется электрону, чтобы пересечь область?
Показать решение
Водитель скорой помощи везет пациента в больницу. Двигаясь со скоростью 72 км/ч, она замечает, что светофор на предстоящем перекрестке загорелся желтым. Чтобы добраться до перекрестка до того, как загорится красный свет, она должна проехать 50 м за 2,0 с. а) Какое минимальное ускорение должна иметь машина скорой помощи, чтобы добраться до перекрестка до того, как загорится красный сигнал светофора? б) С какой скоростью машина скорой помощи доедет до перекрестка? 9{2} [/латекс]. Затем она движется с постоянной скоростью в течение следующих 5,0 мин. Затем она замедляется с постоянной скоростью так, что через 3,0 мин останавливается в точке B. а) Нарисуйте график зависимости скорости от времени для поездки. б) Чему равно ускорение за последние 3 мин? в) Какое расстояние проехал велосипедист?
б) Чему равно ускорение за последние 3 мин? в) Какое расстояние проехал велосипедист?
Два поезда движутся со скоростью 30 м/с в противоположных направлениях по одному и тому же пути. Инженеры одновременно видят, что они находятся на встречном курсе, и включают тормоза, когда расстояние между ними составляет 1000 м. Предполагая, что оба поезда имеют одинаковое ускорение, каким должно быть это ускорение, чтобы поезда остановились перед столкновением?
Показать решение
Грузовой автомобиль длиной 10,0 м, движущийся с постоянной скоростью 97,0 км/ч, проезжает автомобиль длиной 3,0 м, движущийся с постоянной скоростью 80,0 км/ч. Сколько времени проходит между моментом, когда передняя часть грузовика окажется на одном уровне с задней частью автомобиля, и моментом, когда задняя часть грузовика окажется на одном уровне с передней частью автомобиля?
Полицейская машина спряталась немного в стороне от шоссе. Полицейская машина замечает мчащуюся машину, которая движется со скоростью 40 м/с.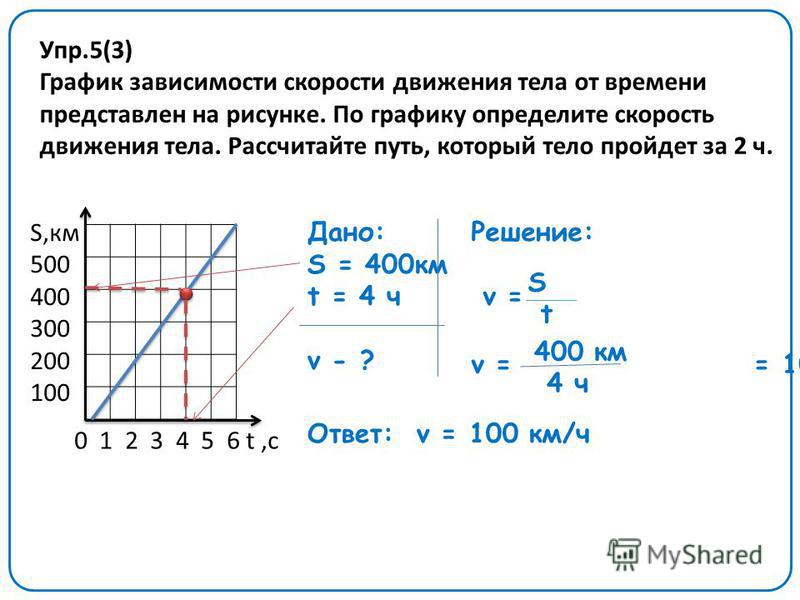 В момент, когда мчащаяся машина проезжает мимо полицейской машины, полицейская машина ускоряется из состояния покоя со скоростью 4 м/с 2 , чтобы поймать мчащуюся машину. Сколько времени потребуется полицейской машине, чтобы догнать мчащуюся машину?
В момент, когда мчащаяся машина проезжает мимо полицейской машины, полицейская машина ускоряется из состояния покоя со скоростью 4 м/с 2 , чтобы поймать мчащуюся машину. Сколько времени потребуется полицейской машине, чтобы догнать мчащуюся машину?
Показать решение
Пабло бежит полумарафон со скоростью 3 м/с. Другой бегун, Джейкоб, с такой же скоростью отстает от Пабло на 50 метров. Джейкоб начинает ускоряться со скоростью 0,05 м/с 2 . а) Сколько времени потребуется Джейкобу, чтобы поймать Пабло? б) Какое расстояние преодолел Иаков? в) Какова конечная скорость Якова?
Необоснованные результаты Бегун приближается к финишу и находится на расстоянии 75 м; ее средняя скорость в этом положении 8 м/с. В этот момент она замедляется со скоростью 0,5 м/с 2 . За какое время она пересечет финишную черту с расстояния 75 м? Это разумно?
Показать решение
Самолет разгоняется до 5,0 м/с 2 за 30,0 с. За это время он преодолевает расстояние 10,0 км. Каковы начальная и конечная скорости самолета?
За это время он преодолевает расстояние 10,0 км. Каковы начальная и конечная скорости самолета?
Сравните расстояние, пройденное объектом, скорость которого изменилась в два раза по сравнению с начальной скоростью, с объектом, скорость которого изменилась в четыре раза по сравнению с начальной скоростью за тот же период времени. Ускорения обоих тел постоянны.
Показать решение
Объект движется на восток с постоянной скоростью и находится в положении [латекс] {x}_{0}\,\text{at}\,\text{time}\,{t}_{0}=0 [/латекс]. а) Какое ускорение должен иметь объект, чтобы его полное перемещение стало равным нулю через t ? (b) Какова физическая интерпретация решения для случая [латекс] t\to \infty [/латекс]?
Мяч брошен прямо вверх. На своем пути вверх он проходит окно высотой 2,00 м на высоте 7,50 м от земли, и ему требуется 1,30 с, чтобы пройти мимо окна. Какова была начальная скорость мяча?
Показать решение
Монета сбрасывается с воздушного шара, находящегося на высоте 300 м над землей и поднимающегося вверх со скоростью 10,0 м/с.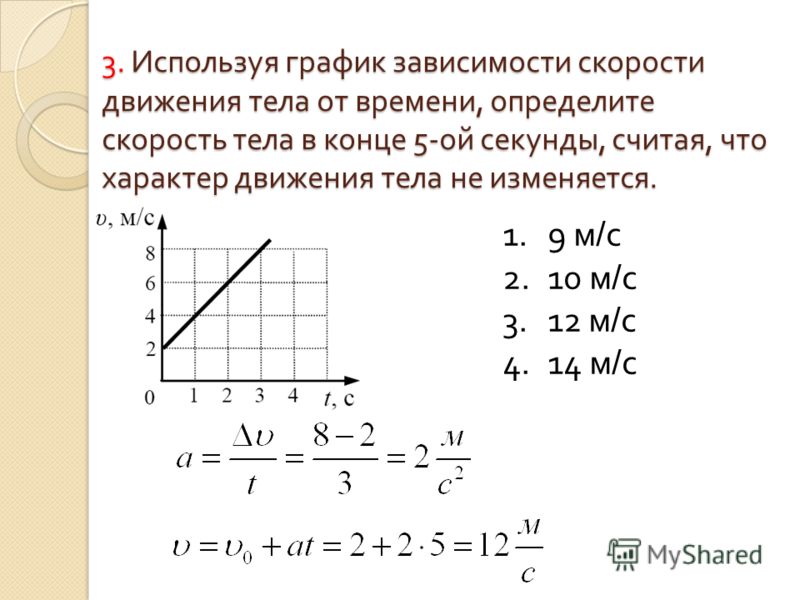 {-3}\,\text{s}) [/латекс] (d) Насколько сильно сжался мяч при ударе о пол, если предположить, что пол абсолютно жесткий?
{-3}\,\text{s}) [/латекс] (d) Насколько сильно сжался мяч при ударе о пол, если предположить, что пол абсолютно жесткий?
Показать решение
Необоснованные результаты . Капля дождя падает из облака на высоте 100 м над землей. Сопротивлением воздуха пренебречь. Какова скорость капли дождя в момент удара о землю? Это разумное число?
Сравните время нахождения в воздухе баскетболиста, прыгнувшего с пола на 1,0 м вертикально, со временем игрока, прыгнувшего на 0,3 м вертикально.
Показать решение
Предположим, что человеку требуется 0,5 с, чтобы среагировать и пошевелить рукой, чтобы поймать предмет, который он уронил. (а) Как далеко объект падает на Землю, где [латекс] g = 9{2}? [/latex] (b) Как далеко падает объект на Луне, где ускорение свободного падения составляет 1/6 от земного?
Воздушный шар поднимается над землей с постоянной скоростью 3,0 м/с. Через минуту после старта с воздушного шара случайно сбрасывается мешок с песком. Вычислите: а) время, за которое мешок с песком достигает земли, и б) скорость мешка с песком в момент удара о землю.
Вычислите: а) время, за которое мешок с песком достигает земли, и б) скорость мешка с песком в момент удара о землю.
Показать решение
(a) Мировой рекорд в беге на 100 м среди мужчин на Олимпийских играх 2008 года в Пекине был установлен Усэйном Болтом с Ямайки. Болт пересек финишную черту со временем 9.0,69 с. Если мы предположим, что Болт ускорялся в течение 3,00 с, чтобы достичь своей максимальной скорости, и поддерживал эту скорость до конца гонки, рассчитайте его максимальную скорость и его ускорение. (b) Во время той же Олимпиады Болт также установил мировой рекорд в беге на 200 м со временем 19,30 с. Используя те же предположения, что и для бега на 100 м, какова была его максимальная скорость в этом забеге?
Предмет падает с высоты 75,0 м над уровнем земли. а) Определите путь, пройденный за первую секунду. б) Определить конечную скорость, с которой тело упадет на землю. в) Определите расстояние, пройденное за последнюю секунду движения до удара о землю. 9{-5}\,\text{s}) [/latex] (d) Насколько сильно сжался мяч при ударе о пол, если предположить, что пол абсолютно жесткий?
9{-5}\,\text{s}) [/latex] (d) Насколько сильно сжался мяч при ударе о пол, если предположить, что пол абсолютно жесткий?
Предмет падает с крыши здания высотой ч . За последнюю секунду своего спуска он преодолел расстояние ч /3. Рассчитайте высоту здания.
Показать решение
Задачи-вызовы
В забеге на 100 м победитель показывает время 11,2 с. Время второго места – 11,6 с. Как далеко занявшая второе место отстаёт от победительницы, когда она пересекает финишную черту? Предположим, что скорость каждого бегуна постоянна на протяжении всего забега. 9{3} [/латекс] м. Найти: а) скорость и ускорение частицы как функции времени, б) скорость и ускорение в t = 2,0 с, в) время, когда положение максимально, г) время скорость которого равна нулю, и (e) максимальное положение.
Показать решение
Велосипедист мчится в конце гонки, чтобы одержать победу. Она имеет начальную скорость 11,5 м/с и ускоряется со скоростью 0,500 м/с 2 за 7,00 с. а) Какова его конечная скорость? (b) Велосипедист продолжает движение с этой скоростью до финиша. Если она находится в 300 м от финиша, когда начинает разгоняться, сколько времени она сэкономила? (c) Победитель, занявший второе место, был на 5,00 м впереди, когда победитель начал ускоряться, но он не смог ускориться и двигался со скоростью 11,8 м/с до финиша. Какая разница во времени финиша в секундах между победителем и призером? Как далеко от финиша финишировал занявший второе место?
а) Какова его конечная скорость? (b) Велосипедист продолжает движение с этой скоростью до финиша. Если она находится в 300 м от финиша, когда начинает разгоняться, сколько времени она сэкономила? (c) Победитель, занявший второе место, был на 5,00 м впереди, когда победитель начал ускоряться, но он не смог ускориться и двигался со скоростью 11,8 м/с до финиша. Какая разница во времени финиша в секундах между победителем и призером? Как далеко от финиша финишировал занявший второе место?
В 1967 году новозеландец Берт Манро установил мировой рекорд для индийского мотоцикла на соляных равнинах Бонневиль в штате Юта, со скоростью 295,38 км/ч. Длина трассы в один конец составила 8,00 км. Темпы ускорения часто описываются временем, которое требуется для достижения 96,0 км/ч из состояния покоя. Если это время составило 4,00 с, и Берт разогнался с такой скоростью, пока не достиг своей максимальной скорости, сколько времени потребовалось Берту, чтобы пройти этот путь?
Показать решение
График u-t движущегося объекта показан на рисунке.
 авеню Турито
авеню ТуритоВы уверены, что хотите выйти?
Вопрос
- 0
- 2,5 мс –1
- 5 мс –1
- 2 мс –1
Правильный ответ: 0
Поскольку полное перемещение равно нулю, значит, средняя скорость также равна нулю0005
физика-
Из следующего графика перемещение-время найдите скорость движущегося тела
- 3 м/с
- м/с
- м/с
Из следующего графика перемещение-время найдите скорость движущегося тела
Общая физика
- 3 м/с
- м/с
- м/с
Общие
Физика-
График ускорения тела во времени показан ниже
Наиболее вероятный график скорости тела во времени
График ускорения тела во времени показан ниже
Наиболее вероятный график скорости тела во времени
Общая физика
Общие
Физика-
Данный график показывает изменение скорости с перемещением.
 Какой из приведенных ниже графиков правильно представляет изменение ускорения при перемещении
Какой из приведенных ниже графиков правильно представляет изменение ускорения при перемещении Данный график показывает изменение скорости с перемещением. Какой из приведенных ниже графиков правильно представляет изменение ускорения при перемещении
Общая физика
Общие
Физика-
Показан график ускорение-время тела. Соответствующий график зависимости скорости от времени того же тела:
Показан график ускорения тела от времени. Соответствующий график зависимости скорости от времени того же тела равен
Общая физика
Общий
Физика-
Поезд идет от одной станции до другой за 2 часа. График его скорости во времени при этом движении показан на рисунке.
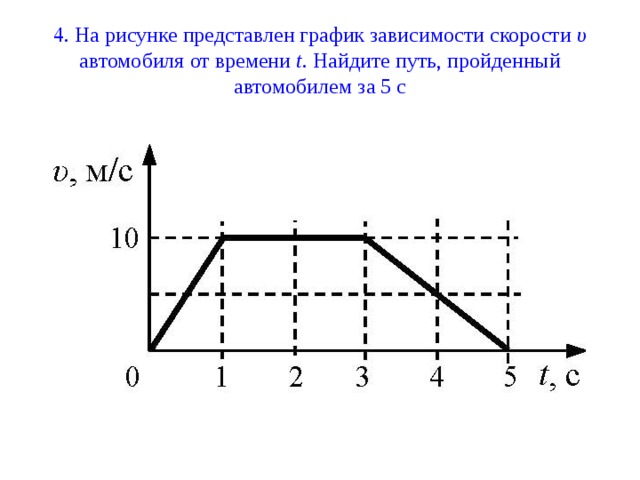 Максимальное ускорение в пути
Максимальное ускорение в пути - 100 км ч –2
- 160 км ч –2
- 120 км ч –2
- 140 км ч –2
Поезд идет с одной станции на другую за 2 часа. График его скорости во времени при этом движении показан на рисунке. Максимальное ускорение в пути
физика-общая
- 100 км ч –2
- 160 км ч –2
- 120 км ч –2
- 140 км ч –2
Общий
Физика-
График зависимости смещения от времени Соответствующий график зависимости скорости от времени будет
График зависимости смещения от времени Соответствующий график зависимости скорости от времени будет
Общие
Физика-
Мяч падает вертикально с высоты над землей.
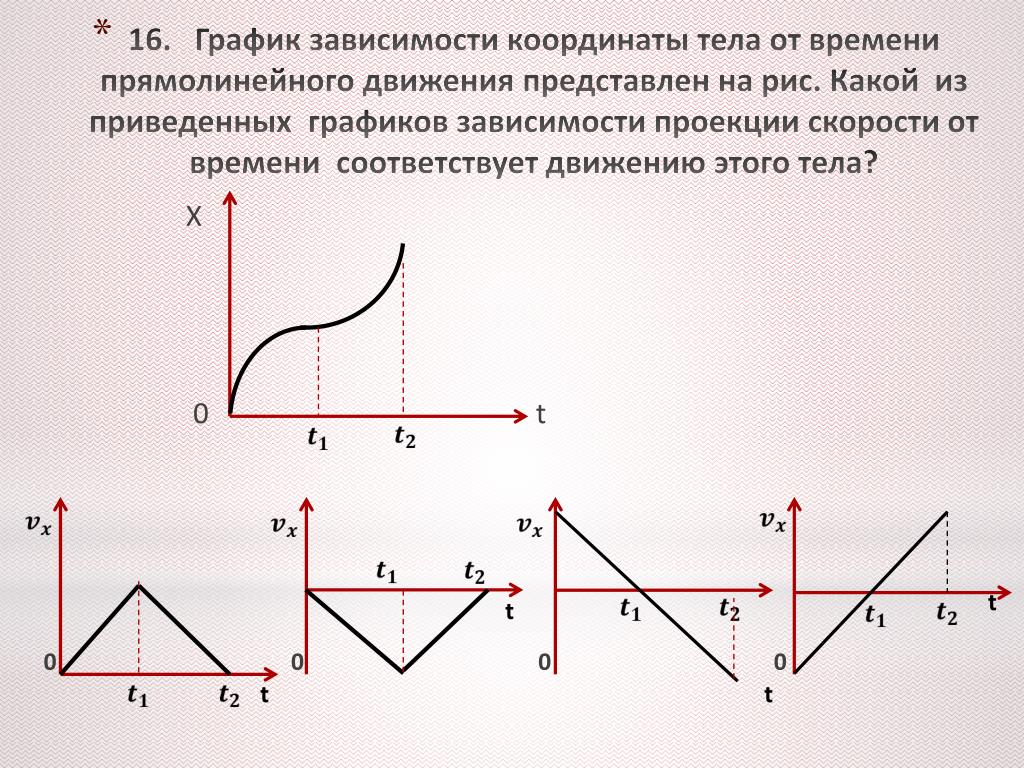 Он ударяется о землю и подпрыгивает вертикально на высоту. Если пренебречь последующим движением и сопротивлением воздуха, его скорость зависит от высоты над землей:
Он ударяется о землю и подпрыгивает вертикально на высоту. Если пренебречь последующим движением и сопротивлением воздуха, его скорость зависит от высоты над землей:- Нет
Мяч падает вертикально с высоты над землей. Он ударяется о землю и подпрыгивает вертикально на высоту. Если пренебречь последующим движением и сопротивлением воздуха, его скорость меняется с высотой над землей на
Общая физика
- Нет
Общие
Физика-
Ниже показан график зависимости перемещения движущейся частицы от времени
Мгновенная скорость частицы в точке отрицательна
- D
- Ф
- Э
- С
График перемещения движущейся частицы от времени показан ниже
Мгновенная скорость частицы в точке отрицательна
Общая физика
- D
- Ф
- Э
- С
Общее
Физика-
На следующем графике расстояние, пройденное телом в метрах, равно
- 250
- 200
- 300
- 400
На следующем графике расстояние, пройденное телом в метрах, равно
Общая физика
- 250
- 200
- 300
- 400
Общий
Физика-
Для графика скорость-время, показанного на рисунке ниже, расстояние, пройденное телом за последние две секунды его движения, представляет собой долю общего расстояния, пройденного им за все семь секунд
Для графика скорость-время, показанного на рисунке ниже, расстояние, пройденное телом за последние две секунды его движения, составляет долю от общего расстояния, пройденного им за все семь секунд
Общая физика
Общий
Физика-
График зависимости скорости от времени (v-t) движущегося объекта показан на рисунке.
 Полное перемещение объекта за интервал времени, когда имеет место ненулевое ускорение и замедление, составляет
Полное перемещение объекта за интервал времени, когда имеет место ненулевое ускорение и замедление, составляет - 60 м.
- 40 м
- 50 м
- 30 м
График зависимости скорости от времени (v-t) для движущегося объекта показан на рисунке. Суммарное перемещение объекта за интервал времени, когда имеются ненулевые ускорения и замедления, равно
физика общая
- 60 м
- 40 м
- 50 м
- 30 м
Общие
Физика-
График зависимости скорости тела, движущегося прямолинейно, показан на рисунке. Перемещение и путь, пройденный телом за 6 с, равны соответственно
- 16 м, 16 м.
- 8 м, 8 м
- 16 м, 8 м
- 8 м, 16 м
График зависимости скорости тела, движущегося прямолинейно, показан на рисунке. Перемещение и путь, пройденный телом за 6 с, составляют соответственно
общая физика
- 16 м, 16 м.

- 8 м, 8 м
- 16 м, 8 м
- 8 м, 16 м
Общий
Физика-
Лифт поднимается. Изменение скорости лифта показано на графике. На какую высоту лифт поднимает пассажиров
- 3,6
- 36,0
- Невозможно рассчитать по приведенному выше графику
- 28,8
Лифт поднимается. Изменение скорости лифта показано на графике. На какую высоту лифт поднимает пассажиров
физика-общая
- 3.6
- 36,0
- Невозможно рассчитать по приведенному выше графику
- 28,8
Общие
Физика-
График, показанный на рисунке, представляет
- Скорость тела непрерывно изменяется
- Тело движется с постоянной скоростью до определенного времени, а затем останавливается
- Мгновенная скорость
- Постоянная скорость
График, показанный на рисунке, представляет
Общая физика
- Скорость тела постоянно меняется
- Тело движется с постоянной скоростью до определенного времени, а затем останавливается
- Мгновенная скорость
- Постоянная скорость
Общие
Физика-
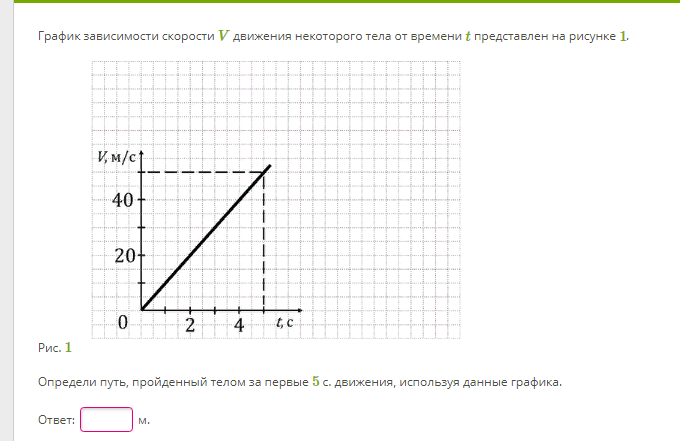
График зависимости смещения от времени для тела, движущегося прямолинейно, показан на рисунке.


Leave A Comment