Грузовик массой м движущийся по прямолинейному горизонтальному участку: EF18051 | СПАДИЛО

Грузовик массой m, движущийся по прямолинейномугоризонтальному участку дороги со скоростью совершаетторможение до полной остановки. Физика 18051

Задание 18051

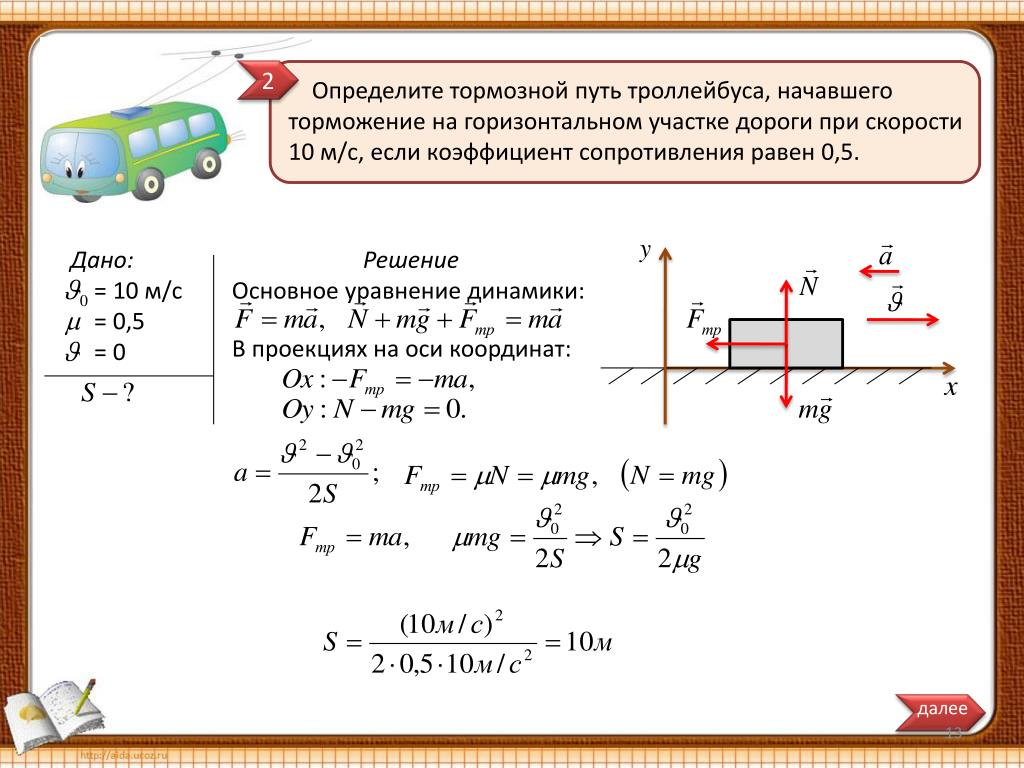
Грузовик массой m, движущийся по прямолинейному горизонтальному участку дороги со скоростью  совершает торможение до полной остановки. При торможении колёса грузовика не вращаются. Коэффициент трения между колёсами и дорогой равен μ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

	ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ		ФОРМУЛЫ
А)	модуль силы трения, действующей на грузовик	1)	μmg
Б)	тормозной путь грузовика	2)	μg
		3)	υμg
		4)	υ22μg

14

Задание 17625 Задание 17647 Задание 18051 Задание 18086 Задание 18204 Задание 18261 Задание 18428 Задание 18447 Задание 18461 Задание 18493

404 Not Found

404 Not Found

О себе Кормаков Н. А. Публикации Методические материалы Статья «Знаю все способы списывания» Статья «Школа этикета» Материал «Первое сентября» Финская школа Классы 7 класс Опорные конспекты Тесты для самоконтроля Тренировочные задания Контрольные работы Итоговые тесты 8 класс Опорные конспекты Тесты для самоконтроля Тренировочные задания Контрольные работы Итоговые тесты 9 класс Опорные конспекты Тесты для самоконтроля Тренировочные задания Контрольные работы Итоговые тесты 10 класс Опорные конспекты Тренировочные задания Итоговые тесты Контрольные работы 11 класс Опорные конспекты Тренировочные задания Итоговые тесты Контрольные работы Порешаем!!! 7 — 9 классы Повышенный уровень

ОГЭ-2021 По номерам заданий Задания по физическим явлениям Тренировочные задания ЕГЭ-2022 Часть — 1 Часть — 2 Часть -3

8.

3 Упругие и неупругие столкновения

Цели обученияУпругие и неупругие столкновенияРешение проблем столкновенийПрактические задачиПроверьте свое понимание

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Различать упругие и неупругие столкновения
• Решите задачи о столкновениях, применив закон сохранения импульса

Основные термины раздела

упругое столкновение	неупругое столкновение	точечных масс
отдача

Упругие и неупругие столкновения

При столкновении объекты могут либо слипаться, либо отскакивать друг от друга, оставаясь отдельными. В этом разделе мы рассмотрим эти два разных типа столкновений, сначала в одном измерении, а затем в двух измерениях.

При упругом столкновении объекты разделяются после удара и не теряют своей кинетической энергии. Кинетическая энергия — это энергия движения, и она подробно описана в другом месте. Здесь очень полезен закон сохранения количества движения, и его можно использовать всякий раз, когда результирующая внешняя сила, действующая на систему, равна нулю. На рис. 8.6 показано упругое столкновение, при котором импульс сохраняется.

Рис. 8.6 На диаграмме показано одномерное упругое столкновение двух объектов.

Анимацию упругого столкновения шаров можно увидеть, посмотрев это видео. Он воспроизводит упругие столкновения между шарами разной массы.

Совершенно упругие столкновения могут происходить только с субатомными частицами. Ежедневно наблюдаемых примеров идеально упругих столкновений не существует — часть кинетической энергии всегда теряется, поскольку она преобразуется в теплопередачу из-за трения. Однако столкновения между повседневными объектами почти идеально эластичны, когда они происходят с объектами и поверхностями, которые почти не имеют трения, например, с двумя стальными блоками на льду.

Теперь для решения задач, связанных с одномерными упругими столкновениями двух объектов, мы можем использовать уравнение сохранения импульса. Во-первых, уравнение сохранения количества движения двух тел при одномерном столкновении имеет вид

.

p1+p2=p′1+p′2 (Fnet=0).p1+p2=p′1+p′2 (Fnet=0).

Подставляя определение импульса p = m v для каждого начального и конечного импульсов, получаем

m1v1+m2v2=m1v′1+m2v′2,m1v1+m2v2=m1v′1+m2v′2,

, где штрихи (‘) обозначают значения после столкновения; В некоторых текстах вы можете увидеть i для начального (до столкновения) и f для конечного (после столкновения). Уравнение предполагает, что масса каждого объекта не меняется во время столкновения.

Watch Physics

Импульс: фигурист бросает мяч

В этом видео рассматривается задача об упругом столкновении, в которой мы находим скорость отдачи фигуриста, бросающего мяч прямо вперед. Чтобы уточнить, Сал использует уравнение

mball Vball + mskater Vskater=mball v′ball + mskater v’skatermball Vball + mskater Vskater=mball v′ball + mskater v’skater.

Щелкните, чтобы просмотреть содержание

Проверка захвата

Результирующий вектор сложения векторов a→ и b→ равен r→. Величины a→, b→ и r→ равны A, B и R соответственно. Какие из следующих утверждений верно?

1. Rx+Ry=0
2. Топор+Ау=А→
3. Ax+By=Bx+Ay
4. Ax+Bx=Rx

Теперь обратимся ко второму типу столкновения. Неупругое столкновение — это столкновение, при котором объекты слипаются после удара, а кинетическая энергия сохраняется , а не . Это отсутствие сохранения означает, что силы между сталкивающимися объектами могут преобразовывать кинетическую энергию в другие формы энергии, такие как потенциальная энергия или тепловая энергия. Понятия энергии обсуждаются более подробно в другом месте. При неупругих столкновениях кинетическая энергия может теряться в виде тепла. На рис. 8.7 показан пример неупругого столкновения. Два объекта с одинаковой массой движутся навстречу друг другу с одинаковой скоростью, а затем слипаются. Два объекта останавливаются после слипания, сохраняя импульс, но не кинетическую энергию после столкновения. Часть энергии движения преобразуется в тепловую энергию или тепло.

Рис. 8.7 Одномерное неупругое столкновение двух объектов. Импульс сохраняется, но кинетическая энергия не сохраняется. а) Два тела одинаковой массы первоначально движутся навстречу друг другу с одинаковой скоростью. (b) Объекты слипаются, создавая совершенно неупругое столкновение. В случае, показанном на этом рисунке, объединенные объекты останавливаются; Это верно не для всех неупругих столкновений.

Поскольку два объекта слипаются после столкновения, они движутся вместе с одинаковой скоростью. Это позволяет упростить уравнение сохранения импульса из

m1v1+m2v2=m1v′1+m2v′2m1v1+m2v2=m1v′1+m2v′2

от

до

m1v1+m2v2= (m1+m2)v’m1v1+m2v2= (m1+m2)v’

для неупругих столкновений, где v ′ — конечная скорость обоих объектов, когда они слипаются, либо в движении, либо в состоянии покоя.

Watch Physics

Введение в импульс

В этом видео рассматриваются определения импульса и импульса. Также рассматривается пример использования закона сохранения импульса для решения задачи о неупругом столкновении автомобиля с постоянной скоростью и неподвижного грузовика. Обратите внимание, что Сал случайно называет единицей измерения импульса джоули; на самом деле это N⋅⋅с или к⋅⋅г/с.

Щелкните, чтобы просмотреть содержание

Проверка сцепления

Как изменится конечная скорость системы легковой автомобиль-грузовик, если бы грузовик имел некоторую начальную скорость, движущуюся в том же направлении, что и автомобиль? Что, если бы грузовик изначально двигался в направлении, противоположном легковому? Почему?

1. Если бы грузовик изначально двигался в том же направлении, что и автомобиль, конечная скорость была бы больше. Если бы грузовик изначально двигался в направлении, противоположном легковому, конечная скорость была бы меньше.
2. Если бы грузовик изначально двигался в том же направлении, что и автомобиль, конечная скорость была бы меньше. Если бы грузовик изначально двигался в направлении, противоположном легковому, конечная скорость была бы больше.
3. Направление, в котором изначально двигался грузовик, значения не имеет. Если бы грузовик изначально двигался в любом направлении, конечная скорость была бы меньше.
4. Направление, в котором изначально двигался грузовик, значения не имеет. Если бы грузовик изначально двигался в любом направлении, конечная скорость была бы больше.

Snap Lab

Кубики льда и упругие столкновения

В этом упражнении вы будете наблюдать за упругим столкновением, вставляя кубик льда в другой кубик льда на гладкой поверхности, так что незначительное количество энергии преобразуется в тепло.

Материалы:

• Несколько кубиков льда (Лед должен быть в форме кубиков. )
• Гладкая поверхность

Процедура:

1. Найдите несколько кубиков льда примерно одинакового размера и гладкую кухонную столешницу или стол со стеклянной столешницей.
2. Положите кубики льда на поверхность на расстоянии нескольких сантиметров друг от друга.
3. Подбросьте один кубик льда к неподвижному кубику льда и наблюдайте траекторию и скорость кубиков льда после столкновения. Старайтесь избегать боковых столкновений и столкновений с вращающимися кубиками льда.
4. Объясните скорости и направления кубиков льда, используя импульс.

Проверка захвата

Было ли столкновение упругим или неупругим?

1. идеально эластичный
2. абсолютно неэластичный
3. Почти идеальная эластичность
4. Почти идеальная неэластичность

Советы по достижению успеха

Вот уловка, позволяющая запомнить, какие столкновения являются упругими, а какие неупругими: Эластичный материал — это упругий материал, поэтому когда объекты отскакивают друг от друга при столкновении и разделяются, это упругое столкновение. Когда их нет, столкновение неупругое.

Решение проблем столкновений

Видео Академии Хана, упомянутые в этом разделе, показывают примеры упругих и неупругих столкновений в одном измерении. В одномерных столкновениях входящая и исходящая скорости лежат на одной линии. А как насчет столкновений, например, между бильярдными шарами, при которых предметы разлетаются в стороны? Это двумерные столкновения, и так же, как мы делали это с двумерными силами, мы решим эти проблемы, выбрав сначала систему координат и разделив движение на его 9 частей.Компоненты 0053 x и y .

Одна из сложностей с двумерными столкновениями заключается в том, что объекты могут вращаться до или после столкновения. Например, если два фигуриста берутся за руки, проходя мимо друг друга, они будут вращаться по кругу. Такой поворот мы будем рассматривать позже, а пока устроим так, что поворот невозможен. Чтобы избежать вращения, мы рассматриваем только рассеяние точечных масс, то есть бесструктурных частиц, которые не могут вращаться или вращаться.

Начнем с предположения, что F _net = 0, так что импульс p сохраняется. Простейшим столкновением является такое, при котором одна из частиц изначально покоится. Наилучший выбор системы координат — с осью, параллельной скорости приближающейся частицы, как показано на рис. 8.8. Поскольку импульс сохраняется, компоненты импульса вдоль осей x и y отображаются как p _x и p _y , также будут сохранены. В выбранной системе координат p _y изначально равно нулю, а p _x является импульсом налетающей частицы.

Рис. 8.8 Двумерное столкновение с системой координат, выбранной так, что м ₂ изначально покоятся, а v ₁ параллельны оси x .

Теперь возьмем уравнение сохранения импульса, P ₁ + P ₂ = P ′ ₁ + P ′ ₂ и разбейте его на x и 4434444444444444444444444444444444444444444444444444444444444444444444444444444444443.

Вдоль оси x уравнение сохранения импульса имеет вид

p1x+p2x=p’1x+p’2x.p1x+p2x=p’1x+p’2x.

В терминах масс и скоростей это уравнение равно

8.3 m1v1x+m2v2x=m1v′1x+m2v′2x.m1v1x+m2v2x=m1v′1x+m2v′2x.

Но поскольку частица 2 изначально покоится, это уравнение принимает вид

8.4 m1v1x=m1v′1x+m2v′2x.m1v1x=m1v′1x+m2v′2x.

Компоненты скоростей вдоль оси x имеют вид v cos θ . Поскольку частица 1 изначально движется вдоль оси x , мы находим v _{1 x} = v ₁ . Сохранение импульса вдоль оси x дает уравнение

m1v1=m1v′1cos θ1+m2v′2cos θ2,m1v1=m1v′1cos θ1+m2v′2cos θ2,

, где  θ1  θ1  и  θ2  θ2  такие, как показано на рисунке 8.8.

Вдоль оси y уравнение сохранения импульса имеет вид

8.5p1y+p2y=p’1y+p’2y,p1y+p2y=p’1y+p’2y,

или

8.6m1v1y+m2v2y=m1v′1y+m2v′2y.m1v1y+m2v2y=m1v′1y+m2v′2y.

Но v ₁ y равно нулю, потому что частица 1 изначально движется вдоль оси x . Поскольку частица 2 изначально покоится, v ₂ y тоже ноль. Уравнение сохранения импульса вдоль оси y принимает вид

8,70 =m1v′1y+m2v′2y.0 =m1v′1y+m2v′2y.

Компоненты скоростей вдоль оси y имеют вид v sin θθ. Таким образом, сохранение импульса вдоль оси y дает следующее уравнение:

0=m1v′1sinθ1+m2v′2sinθ20=m1v′1sinθ1+m2v′2sinθ2

Виртуальная физика

Лаборатория столкновений

В этой симуляции вы будете исследовать столкновения на столе для аэрохоккея. Поставьте галочки рядом с параметрами векторов импульсов и диаграмм моментов. Поэкспериментируйте с изменением массы шаров и начальной скорости шара 1. Как это повлияет на импульс каждого шара? А общий импульс? Далее поэкспериментируйте с изменением упругости столкновения. Вы заметите, что столкновения имеют разную степень упругости, от абсолютно упругой до совершенно неупругой.

Рисунок 8.9 Щелкните здесь для моделирования

Проверка захвата

Если вы хотите максимизировать скорость мяча 2 после удара, как бы вы изменили настройки для масс мячей, начальной скорости мяча 1 и упругости параметр? Почему? Подсказка. Установка галочки рядом с векторами скорости и удаление векторов импульса поможет вам визуализировать скорость мяча 2, а нажатие кнопки «Дополнительные данные» позволит вам снять показания.

1. Максимизируйте массу шара 1 и начальную скорость шара 1; минимизировать массу шара 2; и установите эластичность на 50 процентов.
2. Максимизируйте массу шара 2 и начальную скорость шара 1; минимизировать массу шара 1; и установите эластичность на 100 процентов.
3. Максимизируйте массу шара 1 и начальную скорость шара 1; минимизировать массу шара 2; и установите эластичность на 100 процентов.
4. Максимизируйте массу шара 2 и начальную скорость шара 1; минимизировать массу шара 1; и установите эластичность на 50 процентов.

Рабочий пример

Расчет скорости: неупругое столкновение шайбы и вратаря

Найдите скорость отдачи хоккейного вратаря массой 70 кг, который ловит брошенную в него хоккейную шайбу массой 0,150 кг со скоростью 35 м/с. Предположим, что вратарь находится в состоянии покоя перед тем, как поймать шайбу, а трение между льдом и системой шайба-вратарь пренебрежимо мало (см. рис. 8.10).

Рис. 8.10. Хоккеист-вратарь ловит хоккейную шайбу и отскакивает назад при неупругом столкновении.

Стратегия

Импульс сохраняется, поскольку результирующая внешняя сила, действующая на систему «шайба-вратарь», равна нулю. Следовательно, мы можем использовать закон сохранения импульса, чтобы найти конечную скорость системы шайбы и вратаря. Обратите внимание, что начальная скорость вратаря равна нулю, а конечная скорость шайбы и вратаря одинакова.

Решение

Для неупругого столкновения сохранение импульса равно скорости вратаря и шайбы после удара. Поскольку вратарь изначально находится в состоянии покоя, мы знаем, что v ₂ = 0. Это упрощает уравнение до

8,9m1v1= (m1+m2)v′.m1v1= (m1+m2)v′.

Решение для v ′ дает

8,10v′=(m1m1+m2)v1.v′=(m1m1+m2)v1.

Подставляя в это уравнение известные значения, получаем 0,150 кг)(35 м/с)=7,48 × 10-2м/с.

Обсуждение

Эта скорость отдачи мала и направлена ​​в том же направлении, что и первоначальная скорость шайбы.

Рабочий пример

Расчет конечной скорости: упругое столкновение двух тележек

Две твердые стальные тележки сталкиваются лоб в лоб, а затем рикошетят друг от друга в противоположных направлениях на поверхности без трения (см.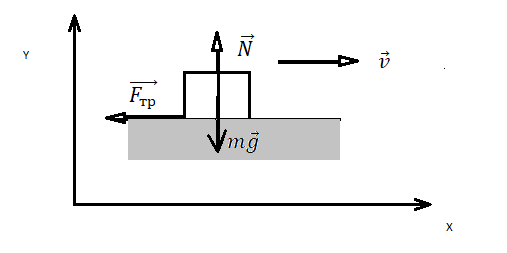 рис. 8.11). Тележка 1 имеет массу 0,350 кг и начальную скорость 2 м/с. Тележка 2 имеет массу 0,500 кг и начальную скорость -0,500 м/с. После столкновения тележка 1 отскакивает со скоростью -4 м/с. Какова конечная скорость тележки 2?

Рис. 8.11 Две тележки сталкиваются друг с другом при упругом столкновении.

Стратегия

Поскольку на пути нет трения, F _сеть = 0, и мы можем использовать закон сохранения импульса, чтобы найти конечную скорость тележки 2.

Решение

Как и прежде, уравнение сохранения импульса для одномерное упругое столкновение в системе из двух объектов равно

8,12m1v1+m2v2=m1v′1+m2v′2.m1v1+m2v2=m1v′1+m2v′2.

Единственным неизвестным в этом уравнении является v ′ ₂ . Решение для v ′ ₂ и подстановка известных значений в предыдущее уравнение дает 0,500 м/с)-(0,350 кг)(-4,00 м/с)0,500 кг=3,70 м/с.v′2=m1v1+m2v2−m1v′1m2=(0,350 кг)(2,00 м/с)+(0,500 кг) (-0,500 м/с)-(0,350 кг)(-4,00 м/с)0,500 кг=3,70 м/с.

Обсуждение

Конечная скорость тележки 2 большая и положительная, что означает, что после столкновения она движется вправо.

Рабочий пример

Расчет конечной скорости при двумерном столкновении

Предположим, проводится следующий эксперимент (рис. 8.12). Предмет массой 0,250 кг ( м ₁ ) скользит по гладкой поверхности в темную комнату, где он сталкивается с изначально неподвижным предметом массой 0,400 кг ( м ₂ ). Объект массой 0,250 кг выходит из комнаты под углом 45º к направлению входа. Скорость объекта массой 0,250 кг изначально равна 2 м/с, а после столкновения — 1,50 м/с. Вычислите модуль и направление скорости ( v ′ ₂ и θ2θ2) объекта массой 0,400 кг после столкновения.

Рис. 8.12 Влетающий объект массой м ₁ рассеивается изначально неподвижным объектом.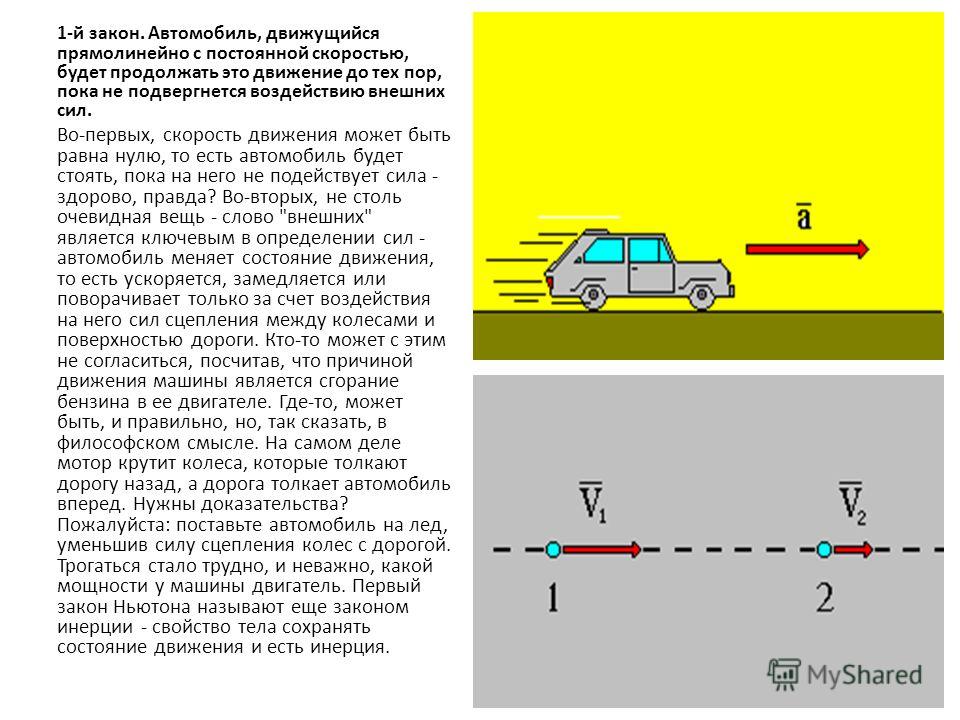 Известна только масса стационарного объекта м ₂ . Измеряя угол и скорость, с которой объект массой м ₁ выходит из комнаты, можно вычислить величину и направление скорости первоначально стационарного объекта после столкновения.

Стратегия

Импульс сохраняется, поскольку на поверхности нет трения. Мы выбрали систему координат так, чтобы начальная скорость была параллельна оси х , и сохранялся импульс вдоль осей х и и .

В этих уравнениях известно все, кроме v ′ ₂ и θ ₂ , которые нам нужно найти. Мы можем найти два неизвестных, потому что у нас есть два независимых уравнения — уравнения, описывающие сохранение импульса в x и y направлений.

Решение

Сначала решим оба уравнения сохранения импульса θ2 0=m1v′1sin θ1+m2v′2sin θ2) для v ′ ₂ sin  θ2 θ2.

Для сохранения импульса вдоль оси x заменим cos θ2θ2 на sin θ2θ2/tan θ2θ2, чтобы позже члены могли сокращаться. Это происходит из-за изменения определения тригонометрического тождества tan θθ = sin θθ/cos θθ. Это дает нам

8.14m1v1=m1v′1cos θ1+m2v′2sin θ2tan θ2.m1v1=m1v′1cos θ1+m2v′2sin θ2tan θ2.

Нахождение v ′ ₂ sinθ2θ2 дает θ2)м2.

Для сохранения импульса вдоль оси y решение для v ′ ₂ sin θ2θ2 дает ′1sin θ1)m2.

Так как оба уравнения равны v ′ ₂ sin θ2θ2, мы можем положить их равными друг другу, что даст θ1)(tan θ2)m2=−(m1v′1sin θ1)m2.

Решая это уравнение относительно тангенса θ2θ2, получаем

Подстановка известных значений в предыдущее уравнение дает 2,00=-1,129.

Следовательно,

8,20θ2=tan−1(−1,129)=3120,θ2=tan−1(−1,129)=3120.

Поскольку углы определяются как положительные в направлении против часовой стрелки, м ₂ рассеивается вправо.

Воспользуемся уравнением сохранения импульса по оси Y, чтобы найти v ′ ₂ . Ввод известных значений в это уравнение дает −0,7485).v′2=−(0,250)(0,400)(1,50)(0,7071−0,7485).

Следовательно,

8,23v′2= 0,886 м/с.v′2= 0,886 м/с.

Обсуждение

Любое уравнение для оси x — или y можно было бы использовать для решения для v ′ ₂ , но уравнение для оси y проще, потому что оно имеет меньше условия.

Практические задачи

При упругом столкновении объект с импульсом 25 кг⋅м/с сталкивается с другим объектом, движущимся вправо, с импульсом 35 кг⋅м/с. После столкновения оба объекта продолжают двигаться вправо, но импульс первого объекта меняется на 10 кг⋅м/с. Чему равен конечный импульс второго объекта?

1. 10кг⋅м/с
2. 20кг⋅м/с
3. 35кг⋅м/с
4. 50кг⋅м/с

При упругом столкновении тело с импульсом 25 кг ⋅ м/с сталкивается с другим телом с импульсом 35 кг ⋅ м/с. Импульс первого объекта изменится на 10 кг ⋅ м/с. Чему равен конечный импульс второго объекта?

1. 10 кг ⋅ м/с
2. 20 кг ⋅ м/с
3. 35 кг ⋅ м/с
4. 50 кг ⋅ м/с

Проверьте свое понимание

Упражнение 8

Что такое упругое столкновение?

1. Упругое столкновение — это столкновение, при котором объекты после удара необратимо деформируются.
2. Упругое столкновение — это столкновение, при котором объекты после удара теряют часть своей внутренней кинетической энергии.
3. Упругое столкновение — это столкновение, при котором объекты после удара не теряют своей внутренней кинетической энергии.
4. Упругое столкновение — это столкновение, при котором объекты после удара слипаются и движутся с общей скоростью.

Упражнение 9

Возможны ли абсолютно упругие столкновения?

1. Совершенно упругие столкновения невозможны.
2. Совершенно упругие столкновения возможны только с субатомными частицами.
3. Совершенно упругие столкновения возможны только тогда, когда объекты слипаются после удара.
4. Совершенно упругие столкновения возможны, если объекты и поверхности почти не имеют трения.

Упражнение 10

Какое уравнение сохранения количества движения двух тел при одномерном столкновении?

1. р ₁ + р ₁ ′ = р ₂ + р 1 _{2 2 9 0}
2. р ₁ + р ₂ = р ₁ ′ + р ₂ ′
3. р ₁ − р ₂ = р ₁ ′ − р ₂ ′
4. р ₁ + р ₂ + р ₁ ′ + р ₂ 0 = 1 0 90 90

• Печать
• Поделиться

Легковой автомобиль массой 2000 кг сталкивается с грузовым автомобилем массой 10^(4) кг, движущимся со скоростью 48 кмcт ч^(-1).

(-1). Какова была скорость автомобиля перед столкновением?

CHHAYA ПУБЛИКАЦИЯ-ЗАКОНЫ ДВИЖЕНИЯ НЬЮТОНА-CBSE СКАНЕР

21 видео

РЕКЛАМА

Ab Padhai каро бина объявления ке

Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!

Обновлено: 27-06-2022

লিখিত জবাব

Решение

После столкновения тело массой m, движущееся со скоростью u, сталкивается с телом массой v по прямой линии и массой v. массы соединяются и движутся со скоростью V. Применяя закон сохранения количества движения.
mu + Mv = (m + M) V
или mu = (m + M) V — Mv
или u=m+MmV−Mmv=(1+Mm)V−Mmv.
Здесь m = 2000 кг, v = 48 км⋅ч-1, M = 10000 кг,
V = 15 км⋅ч-1.
∴ Mm=100002000=5
u = (1 + 5)×15−5×48=90−240=−150км⋅ч−1
Знак минус означает, что до столкновения автомобиль двигался в направлении, противоположном этому грузовика.

Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.

---

সংশ্লিষ্ট ভিডিও

Тяжелый автомобиль A массой 2000 кг, движущийся со скоростью 10 м/с, столкнулся лоб в лоб со спортивным автомобилем B массой 500 кг. Если обе машины остановились при столкновении, какова была скорость машины B?

28396470

एक 100 किग Вивра द्रवNन की क क क क क क क क क क क क क मीट सेकण सेकण के वेग से आक आक 4 मीट सेकण सेकण के वेग से उसी दिश दिश में ज हे किग द्ड के वेग से उसी दिश दिश में में हे किग द दvцин द के के वेग से से उसी दिश दिश में में में ज में. टक्कर के पश्चात् कार 8 मीटर/सेकण्ड के से पीछे लौटती है | टक्कर के पश्चात् ट्रक का वेग कितना होगा ?

94982656

Автомобиль массой 400 кг, движущийся со скоростью 72 км/ч, сталкивается с грузовиком массой 4000 кг, движущимся со скоростью 9 км/ч в том же направлении. Автомобиль отскакивает назад со скоростью 18 км/ч. Какова скорость грузовика после удара?

175528551

एक कार जिसका द्रव्यमान 1000 किगैहडखा खथ पीछे से वेग 10 मी/से से आकर द्रव्यमान 7000 किग्रा का एक ट्रक, कार से टकराता है | यदि टक्कर के पश्चात दोनों गाड़ियाँ एक — दूसरे से जुड़क चलती हैं हैं तो इनक इनक वेग वेग क्या होगा? 9(-1) . Скорость грузовика после удара

642899955

Текст Решение

грузовик движется со скоростью 15 м/с. Автомобиль, преследующий этот грузовик со скоростью 10 м/с, выпускает пулю по грузовику с начальной скоростью 90 км/ч. Скорость, с которой пуля попала в грузовик, равна

644381487

Автомобиль массой 400 кг, движущийся со скоростью 72 км/ч, врезается в грузовик массой 4000 кг, движущийся со скоростью 9 км/ч в том же направлении. Автомобиль отскакивает назад со скоростью 18 км/ч. Скорость грузовика после удара равна

645748026

Текст Решение

Автомобиль движется с равномерной скоростью 54 км/ч. Какова КЭ мальчика массой 40 кг, сидящего в своей машине?

646413576

1000 кг. वह 1200 кг द्रव्यमान की दूस выполнительный टकराने के बाद पहले कार का वेग 15 м/с टक्कर के बाद दूसरे कार का वेग ज्ञात करें।

6465

Текстовое решение

Большой грузовик и легковой автомобиль, движущиеся со скоростью V, столкнулись лоб в лоб, после чего оба остановились.