Отличия перемещения и пути
☰
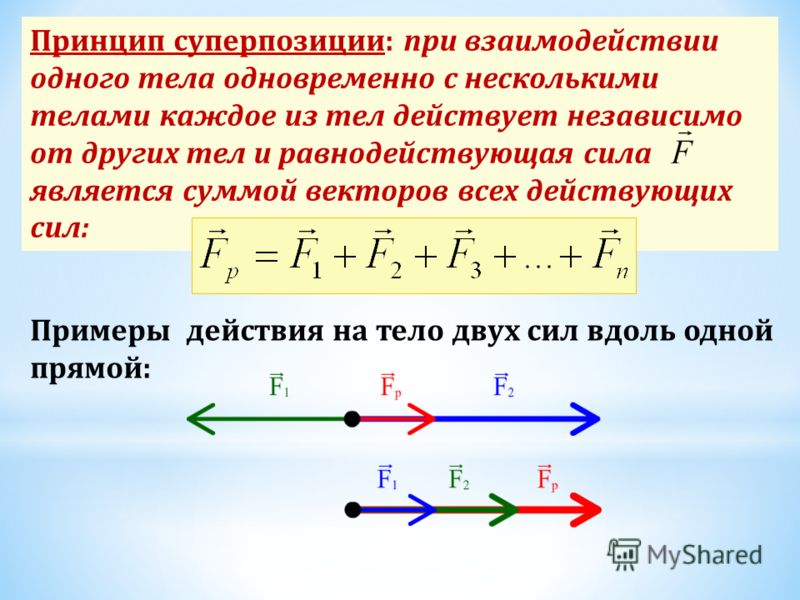
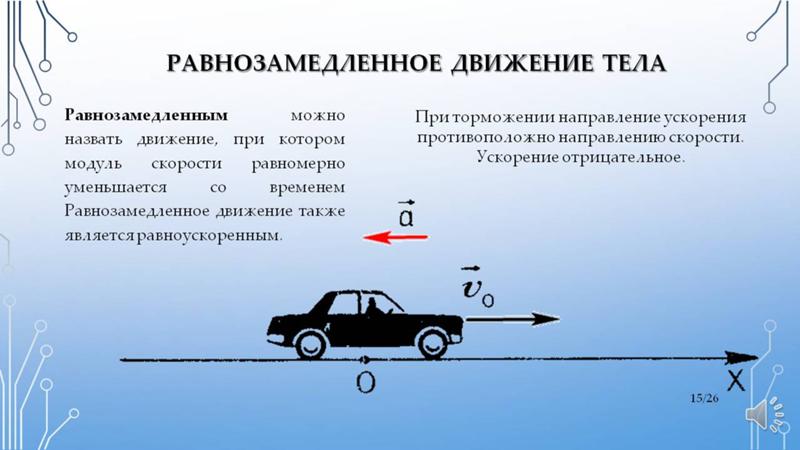
На первый взгляд перемещение и путь — близкие по смыслу понятия. Однако в физике между перемещением и путем есть ключевые отличия, хотя оба понятия связаны с изменением положения тела в пространстве и нередко (обычно при прямолинейном движении) численно равны друг другу.
Чтобы понять отличия перемещения и пути, дадим сначала им определения, которыми их наделяет физика.
Перемещение тела — это направленный отрезок прямой (вектор), начало которого совпадает с начальным положением тела, а конец совпадает с конечным положением тела.
Путь тела — это расстояние, которое прошло тело за определенный промежуток времени.
Представим себе, что вы стали у своего подъезда в определенную точку. Обошли дом и вернулись в исходную точку. Так вот: ваше перемещение будет равно нулю, а путь — не будет. Путь будет равен длине кривой (например, 150 м), по которой вы шли вокруг дома.
Однако вернемся к системе координат. Пусть точечное тело двигается прямолинейно из точки A с координатой x0 = 0 м в точку B с координатой x1 = 10 м. Перемещение тела в данном случае составит 10 м. Так как движение было прямолинейным, то 10-ти метрам будет равен и проделанный телом путь.
Если же тело прямолинейно двигалось из начальной (A) точки с координатой x0 = 5 м, в конечную (B) точку с координатой x1 = 0, то его перемещение составит -5 м, а путь 5 м.
Перемещение находится как разность, где из конечной координаты вычитают начальную. Если конечная координата меньше начальной, т. е. тело двигалось в обратном направлении по отношению к положительному направлению оси X, то перемещение будет отрицательной величиной.
Так как перемещение может иметь как положительное, так и отрицательное значение, то перемещение является векторной величиной. В отличие от него, путь — всегда положительная или равная нулю величина (путь — скалярная величина), так как расстояние не может быть отрицательным в принципе.
Рассмотрим еще один пример. Тело прямолинейно двигалось из точки A (x0 = 2 м) в точку B (x1 = 8 м), далее также прямолинейно из B переместилось в точку C с координатой x2 = 5 м. Чему равны и отличаются ли общий путь (A→B→C) проделанный данным телом и его суммарное перемещение?
Изначально тело было в точке с координатой 2 м, в конце своего движения оказалось в точке, имеющей координату 5 м. Таким образом, перемещение тела составило 5 — 2 = 3 (м). Также можно вычислить общее перемещение как сумму двух перемещений (векторов). Перемещение из A в B составило 8 — 2 = 6 (м). Перемещение из точки B в C составило 5 — 8 = -3 (м). Сложив оба перемещения получим 6 + (-3) = 3 (м).
Общий путь вычисляется путем сложения двух расстояний, прошедших телом. Расстояние от точки A до B составляет 6 м, а от B до C тело проделало путь в 3 м. Итого получаем 9 м.
Таким образом, в данной задаче путь и перемещение тела отличаются между собой.
Рассмотренная задача не совсем корректна, так как необходимо указывать моменты времени, в которые тело находится в определенных точках.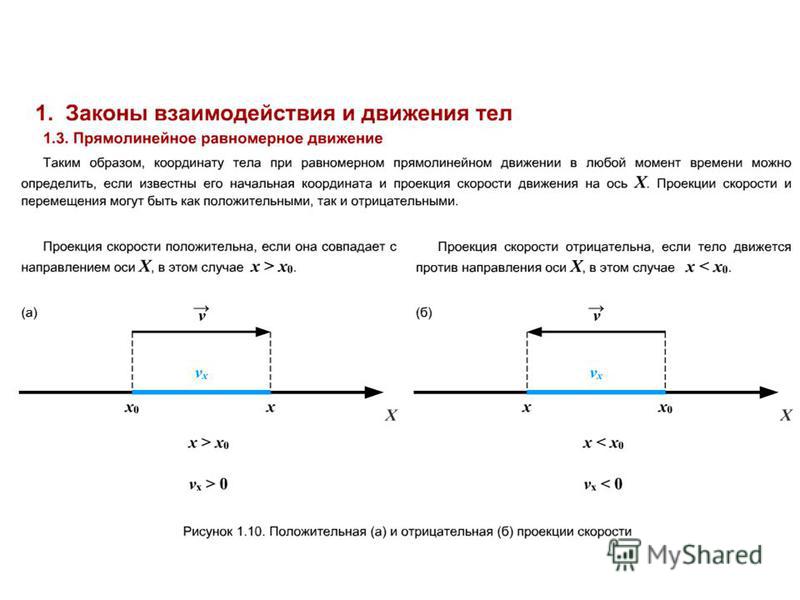 Если x0 соответствует момент времени t0 = 0 (момент начала наблюдений), то пусть например x1 соответствует t1 = 3 c, а x2 соответствует t2 = 5 c. То есть промежуток времени между t0 и t1 составляет 3 с, а между t0 и t2 составляет 5 с. В этом случае получается, что путь тела за промежуток времени в 3 секунды составил 6 метров, а за промежуток в 5 секунд — 9 метров.
Если x0 соответствует момент времени t0 = 0 (момент начала наблюдений), то пусть например x1 соответствует t1 = 3 c, а x2 соответствует t2 = 5 c. То есть промежуток времени между t0 и t1 составляет 3 с, а между t0 и t2 составляет 5 с. В этом случае получается, что путь тела за промежуток времени в 3 секунды составил 6 метров, а за промежуток в 5 секунд — 9 метров.
В определении пути фигурирует время. В отличие от него для перемещения время не имеет особого значения.
11 Facts (Read This First) —
В этой статье мы обсудим 11 фактов, связанных с тем, может ли смещение быть отрицательным или нет.
Ответ на вопрос, может ли смещение быть отрицательным или нет, — да. Мы уточним, как смещение отрицательно. Кратчайшее расстояние между начальным и конечным положением тела можно определить как его перемещение. Перемещение — это всегда прямой путь. Поскольку перемещение является векторной величиной, оно имеет определенное направление.
Перемещение — это всегда прямой путь. Поскольку перемещение является векторной величиной, оно имеет определенное направление.
По этой причине смещение может быть отрицательным. Перемещение любого движущегося тела всегда зависит от его начального и конечного положения, а не от пути, по которому оно шло. На примере покажем, как смещение становится отрицательным. Частица движется вдоль отрицательной оси x, скажем, она переместилась на 50 м вдоль отрицательной оси x. Величина расстояния в данном случае – 50 м. Теперь возникает вопрос, как это было возможно?
Первоначально частица находилась в начале координат. Это означает, что хi = 0, но, в конце концов, он переместился на 50 м по отрицательной оси x. Это означает, что хf = – 50 м т.е., хf< 0. Следовательно, по определению смещение = конечная позиция(xf) – начальное положение(xi) = хf — Иксi = -50 – 0 = – 50 м. В некоторых случаях смещение может быть отрицательным – такой вывод сделан на примере, приведенном выше.
Если тело выбрало движение в отрицательном направлении, то есть оно движется либо вдоль отрицательной оси x, отрицательной оси y, либо отрицательной оси z в трехмерной плоскости, то его перемещение можно назвать отрицательным. Точно так же, если начальное положение тела находится в гораздо более положительном направлении, чем конечное положение, тогда мы также можем сказать, что смещение отрицательно. Теперь опишем это отрицательное смещение на простом математическом примере.
Гусеница идет по стене вниз. Если вначале она была на высоте 57 см, а пройдя расстояние до 20 см, остановилась, то какова будет величина водоизмещения этой гусеницы?
Ответ :
xi = начальное положение гусеницы
xf = конечное положение гусеницы
Итак, изначально гусеница была 57 см. Это означает, что хi = 57 см, а гусеница остановилась на 20 см. Следовательно, хf = 20 см
Мы знаем, что перемещение Δ x = xf — Иксi = 20 см – 57 см = – 37 см
Как мы знаем, когда результат отрицательный, это означает отрицательное смещение. Следовательно, это случай отрицательного смещения.
Следовательно, это случай отрицательного смещения.
Есть несколько условий, когда смещение становится отрицательным. Прежде всего, нам нужно понять одну вещь: когда тело опускается ниже точки, из которой оно изначально начало свое путешествие, тогда такой тип смещения называется отрицательным смещением этого тела.
Теперь еще одну вещь, которую мы должны прояснить здесь. Когда тело движется влево от начала координат, это отрицательное смещение, и если тело падает вниз, пересекая начальную точку в направлении вниз, то это смещение также отрицательно. Как мы знаем, смещение является произведением скорости и времени, следовательно, скорость и ускорение являются факторами смещения. Здесь мы поговорим еще о нескольких условиях, когда смещение отрицательно.
- Когда скорость = 0 и ускорение = – ve
В этом случае сначала тело остается в покое. После этого было выбрано отрицательное направление движения. Итак, это случай отрицательного смещения.
Итак, это случай отрицательного смещения.
- 2. Скорость = – ve и ускорение = +ve
Здесь скорость уменьшается. Таким образом, тело будет двигаться в отрицательном направлении после отрицательного смещения.
- 3. Скорость = – ve и ускорение = 0
В этом случае отрицательного смещения скорость продолжает уменьшаться, и тело движется в отрицательном направлении.
- 4.Скорость = – ve и ускорение = – ve
В этом случае тело также движется в отрицательном направлении после отрицательного смещения.
Как смещение отрицательное?Давайте возьмем простой пример, чтобы понять, как смещение является отрицательным. Допустим, автомобиль находится в состоянии покоя в точке P. Теперь он начинает двигаться в правую сторону до точки Q, которая находится в 10 м справа от точки P, после чего снова начинает двигаться в обратном направлении, то есть в сторону точки P. и достигает точки P. В этом случае автомобиль имеет нулевое водоизмещение. Потому что сначала он переместился на 10 м в правую сторону, а потом снова на 10 м в левую. Отсюда перемещение автомобиля = PQ = 10 – 10 = 0 м.
и достигает точки P. В этом случае автомобиль имеет нулевое водоизмещение. Потому что сначала он переместился на 10 м в правую сторону, а потом снова на 10 м в левую. Отсюда перемещение автомобиля = PQ = 10 – 10 = 0 м.
Теперь, если автомобиль начнет двигаться влево к R, то смещение будет отрицательным. Наверняка возникает вопрос, а почему? Поскольку мы приняли смещение в правой части точки P как положительное смещение, следовательно, смещение вдоль левой стороны точки P должно быть отрицательным. Допустим, R находится в 5 м от P с левой стороны. Отсюда PR = -5 – 0 = – 5 м
Когда смещение не отрицательно?Возможны два случая, когда смещение не является отрицательным. Первый случай имеет нулевое смещение, а второй случай — положительное смещение. Теперь давайте обсудим эти два случая:
- Нулевое смещение
- Положительное смещение
1.
Нулевое смещениеЭто тот случай, когда начальное положение и конечное положение тела накладываются друг на друга.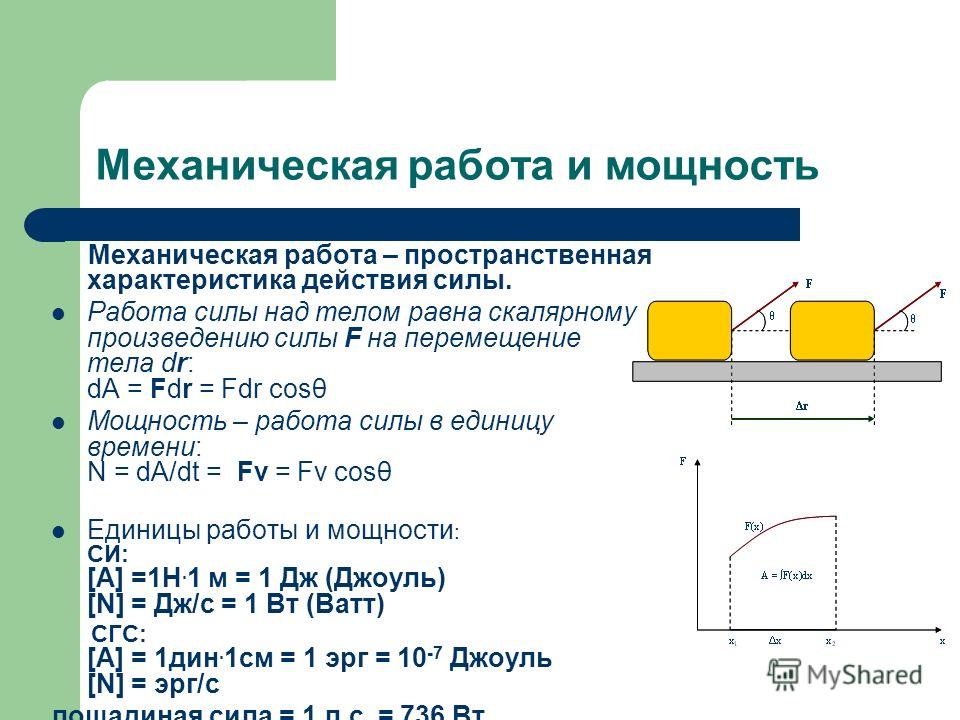 Если xi обозначает начальное положение тела, а xf обозначает конечное положение тела, то перемещение будет = Δ x = xf — Иксi
Если xi обозначает начальное положение тела, а xf обозначает конечное положение тела, то перемещение будет = Δ x = xf — Иксi
В этом случае хi = хf следовательно, Δ х = хf — Иксi = 0
Пример нулевого смещения: если человек начинает двигаться из положения на круглом парке и через некоторое время возвращается в то же положение, то его начальное и конечное положение совпадают. Поэтому ее водоизмещение равно нулю.
2.
Положительное смещениеВ положительном направлении, если конечное положение тела далеко от начального положения, этот случай будет рассматриваться как случай положительного смещения. В этом случае хf> 0 и хi = 0 или xi <0 или xi >0 (но должно иметь меньшее положительное значение, чем xf). В качестве примера положительного перемещения можно рассматривать тело, продолжающее движение вдоль положительной оси x.
- Положительное смещение
В положительном направлении, если конечное положение тела далеко от начального положения, этот случай будет рассматриваться как случай положительного смещения. В этом случае xf> 0 и хi = 0 или хi < 0 или хi >0 (но должно иметь меньшее положительное значение, чем xf). В качестве примера положительного перемещения можно рассматривать тело, продолжающее движение вдоль положительной оси x.
- Отрицательное смещение
Первый случай
Это тот случай, когда начальное положение тела далеко от конечного положения в положительном направлении. Иксi>0 и хf> 0
Δ х = хf — Иксi <0
Второй случай
Может быть и другой случай отрицательного смещения, когда начальное положение тела находится в положительном направлении (положительная ось x), а конечное положение находится в начальной точке (начало координат). Иксi> 0,хf = 0, Δ х = хf — Иксi <0
Иксi> 0,хf = 0, Δ х = хf — Иксi <0
Третий случай
Когда начальное положение тела находится в начале координат, а конечное положение — вдоль отрицательной оси x системы координат. Иксi = 0,хf < 0, Δ х = хf — Иксi <0
Четвертый случай
Когда начальное положение тела находится вдоль положительной оси x, а конечное положение — вдоль отрицательной оси x. Иксi>0,хf<0,
Δ х = хf — Иксi <0
Может ли смещение быть положительным?Это тот случай, когда конечное положение тела далеко от начального положения в положительном направлении. Должен быть другой случай. если тело падает, но не может пересечь исходную точку в направлении вниз, то это перемещение также положительно. В этом случае хf> 0 и хi = 0 или хi < 0 или хi >0 (но должно иметь меньшее положительное значение, чем xf). Пример: частица движется вдоль положительной оси x.
Пример: частица движется вдоль положительной оси x.
Есть несколько условий, когда смещение может быть положительным.
- Когда конечное положение тела далеко от начального положения тела в положительном направлении, то это смещение является положительным смещением.
xi> 0, xf> 0 ∆ x = xf – xi > 0
- Когда конечное положение тела далеко от начального положения в положительном направлении, а начальное положение тела находится в начальной точке, то это случай положительного смещения. Иксi = 0, хf > 0, Δ х = хf — Иксi > 0
- Когда конечное положение тела находится в положительном направлении, тогда как начальное положение тела находится в отрицательном направлении. Иксi< 0, хf > 0
Δ х = хf — Иксi > 0
- Когда конечное положение тела находится в начальной точке, а начальное положение тела находится в отрицательном направлении.
 Иксi < 0, хf = 0
Иксi < 0, хf = 0
Δ х = хf — Иксi > 0
Примеры отрицательного смещенияЕсть несколько примеров отрицательного смещения.
- Частица движется вдоль отрицательной оси x, отрицательной оси y или отрицательной оси z. Смещение этой частицы является примером отрицательного смещения.
- Нили бросила камень вверх. Камень поднялся на 20 м вверх и начал падать на землю. Если он достиг земли, находящейся в 30 м от точки броска вниз, то каково будет его перемещение? Здесь хi = 20 м > 0 и хf = -30 м < 0
Δ х = хf — Иксi = – 30 – 20 = -50 м < 0. Следовательно, смещение камня можно назвать отрицательным смещением.
Примеры положительного смещения- Частица движется вдоль любой из ортогональных осей в положительном направлении, т. е. по положительной оси x, или положительной оси y, или положительной оси z.
 Смещение этой частицы является примером положительного смещения.
Смещение этой частицы является примером положительного смещения. - Возьмем автомобиль, который решил двигаться вдоль отрицательной оси x. Сначала он продвинулся на 10 м, затем снова начал двигаться вправо и достиг 30 м по положительной оси абсцисс. Каким будет его водоизмещение?
Начальное положение автомобиля xi = – 10 м < 0
Конечная позиция автомобиля хf = 30 м > 0
Следовательно, водоизмещение автомобиля равно Δ x = xf — Иксi
= 30 – (-10) м
= (30 + 10) м
= 40 м
Постановка задачи с решением- 1. Частица решила двигаться вдоль вертикальной оси, которая является осью у системы координат.
 Он начал двигаться из точки A вдоль отрицательной оси y. Точка A находится на расстоянии 5 м по отрицательной оси y. После этого эта частица достигла точки, лежащей вдоль положительной оси у на расстоянии 5 м. затем снова частица переместилась в точку С, расположенную по отрицательной оси у на расстоянии 5 м, а оттуда частица переместилась в точку D, расположенную по положительной оси у на расстоянии 5 м. затем снова эта частица переместилась в точку E вдоль отрицательной оси y на расстояние 5 м и, наконец, достигла точки F. каково будет ее полное перемещение?
Он начал двигаться из точки A вдоль отрицательной оси y. Точка A находится на расстоянии 5 м по отрицательной оси y. После этого эта частица достигла точки, лежащей вдоль положительной оси у на расстоянии 5 м. затем снова частица переместилась в точку С, расположенную по отрицательной оси у на расстоянии 5 м, а оттуда частица переместилась в точку D, расположенную по положительной оси у на расстоянии 5 м. затем снова эта частица переместилась в точку E вдоль отрицательной оси y на расстояние 5 м и, наконец, достигла точки F. каково будет ее полное перемещение?
Ответ :
Первоначально частица находилась в точке A вдоль отрицательной оси y. Отсюда его водоизмещение – 5 м. После этого он переместился в точку B вдоль положительной оси y. Теперь его перемещение равно + 5 м, значит, оно достигло точки С по отрицательной оси ординат, значит, его перемещение равно – 5 м.
Начав из точки C, он переместился в точку D вдоль положительной оси y, поэтому перемещение равно + 5 м. Затем он переместился в точку Е по отрицательной оси у, следовательно, перемещение равно – 5 м. наконец она переместилась в точку F. Следовательно, перемещение частицы = (-5 + 5 – 5 + 5 – 5) м = -5 м
Затем он переместился в точку Е по отрицательной оси у, следовательно, перемещение равно – 5 м. наконец она переместилась в точку F. Следовательно, перемещение частицы = (-5 + 5 – 5 + 5 – 5) м = -5 м
Здесь, в этой статье, мы подробно обсудили, может ли смещение быть отрицательным или нет. Помимо этого, мы объяснили отрицательное и положительное смещение с помощью подходящих примеров и математических задач.
Может ли смещение быть отрицательным? (Что это значит и 3 ключевые идеи) — JDM Educational
Смещение используется в математике и физике для описания положения объекта относительно «нулевой» (начальной) точки. Тем не менее, может быть немного сложно ориентироваться в знаках (положительных и отрицательных) смещения, поскольку оно связано с положением.
Итак, может ли смещение быть отрицательным? Смещение объекта может быть отрицательным, например, когда объект падает ниже своей «нулевой» (начальной) высоты. Объект, который начинается с нуля с отрицательной скоростью, будет иметь отрицательное смещение. Отрицательная скорость означает, что смещение объекта уменьшается (движется в отрицательном направлении).
Объект, который начинается с нуля с отрицательной скоростью, будет иметь отрицательное смещение. Отрицательная скорость означает, что смещение объекта уменьшается (движется в отрицательном направлении).
Конечно, отрицательное смещение не является теоретическим, поскольку оно возникает, когда объект падает ниже начальной высоты.
В этой статье мы поговорим об отрицательном смещении и о том, когда оно может произойти. Мы также рассмотрим несколько примеров, чтобы прояснить концепцию.
Начнем.
Может ли смещение быть отрицательным?
Смещение может быть отрицательным в физике или исчислении, например, когда объект падает ниже своей начальной высоты (из-за действия гравитации).
Скорость отрицательна, когда положение уменьшается. В этом случае смещение объекта уменьшается, то есть становится ближе к нулю, если оно положительное, или становится более отрицательным, если оно уже отрицательное.
Важно отметить, что отрицательная скорость (или отрицательное ускорение) не всегда означает отрицательное перемещение. Однако по прошествии достаточного времени отрицательная скорость в конечном итоге приведет к отрицательному смещению.
Однако по прошествии достаточного времени отрицательная скорость в конечном итоге приведет к отрицательному смещению.
В таблице ниже показано, что происходит с ускорением, скоростью и скоростью, когда они имеют разные знаки.
| Velocity | Acceleration | Meaning |
|---|---|---|
| Positive | Positive | Speed is increasing, object goes in positive direction |
| Positive | Zero | Speed is константа, объект движется в положительном направлении |
| положительный | отрицательный | Скорость уменьшается, объект движется in positive direction |
| Zero | Positive | Object at rest about to move in positive direction |
| Zero | Zero | Object at rest |
| Zero | Negative | Объект в состоянии покоя около двигаться в отрицательном направлении |
| отрицательном | положительном | Скорость уменьшается, объект движется in negative direction |
| Negative | Zero | Speed is constant, object goes in negative direction |
| Negative | Negative | Speed is increasing, object goes in negative направление |
ускорением, скоростью и скоростью
, когда они имеют разные знаки.
Что означает отрицательное смещение?
Отрицательное смещение означает, что объект находится ниже своей начальной высоты (или позади или «слева» от своей начальной позиции). Отрицательное смещение указывает на одно из следующего:
- Объект сместился ниже своей начальной высоты (или левее своей начальной позиции на числовой прямой).
- Объект перемещался вверх и вниз (вперед и назад), но сместился вниз на большее расстояние, чем вверх (или назад, чем вперед).
Обратите внимание, что объект с отрицательным смещением может находиться в состоянии покоя (нулевая скорость) или двигаться в положительном направлении (положительная скорость) или в отрицательном направлении (отрицательная скорость).
Отрицательное смещение просто означает, что кумулятивный эффект движения объекта помещает его ниже его начальной высоты (или позади его начального положения).
Объект с отрицательным смещением также может иметь как положительное, так и отрицательное ускорение.
Помните:
- Смещение сообщает нам, где находится объект относительно его «нулевой» (начальной) позиции.
- Скорость говорит нам, как быстро движется объект и в каком направлении.
- Ускорение говорит нам, как быстро объект меняет скорость.
В чем разница между положительным и отрицательным смещением?
Разница между положительным и отрицательным смещением — это положение объекта относительно нулевой или начальной точки:
- Положительное смещение означает, что объект находится выше своей начальной высоты или впереди своего начального положения.
- Отрицательное смещение означает, что объект находится ниже своей начальной высоты или позади своего начального положения.
Смещение не говорит нам, где был объект. Вместо этого он сообщает нам, где находится объект сейчас, в определенное время, относительно того, откуда он начал (нулевое положение).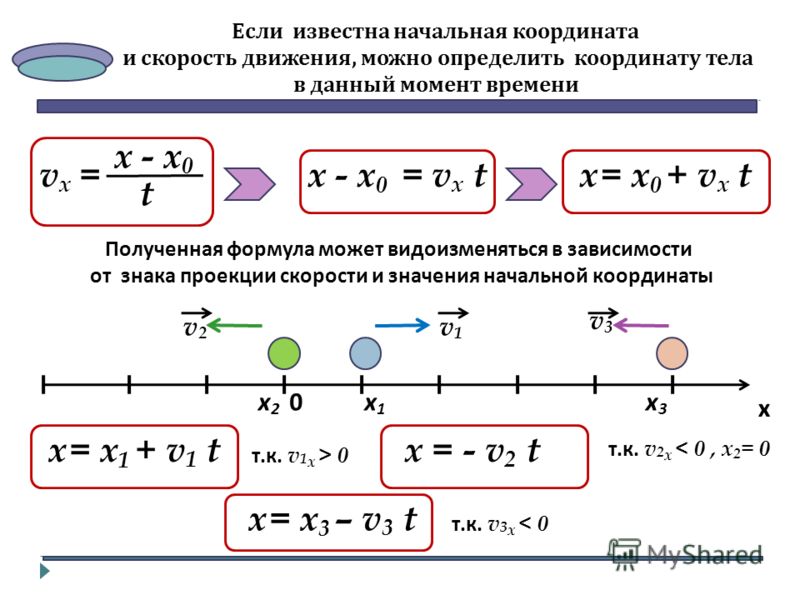
График отрицательного смещения
График ниже показывает смещение объекта во времени:
Смещение (по оси y) положительно от t = 0 до t = 2 (по вертикальной оси). Смещение отрицательно от t = 2 до t = 5. Смещение равно нулю при t = 0 и t = 2.Когда график находится над осью X, смещение положительно, что означает, что объект находится выше начальной высоты. Например, с момента времени t = 0 до момента времени t = 2 объект находится выше своей начальной высоты.
Обратите внимание, что пик графика (в момент времени t = 1) отмечает максимальное расстояние над начальной точкой, которое объект достигает за первые 5 секунд (на 1 единицу выше начальной точки).
Когда график находится ниже оси X, смещение отрицательное, что означает, что объект находится выше начальной высоты. Например, с момента времени t = 2 до момента времени t = 5 объект находится ниже своей начальной высоты.
Обратите внимание, что нижняя часть графика (в момент времени t = 5) отмечает максимальное расстояние ниже начальной точки, которое объект достигает в течение первых 5 секунд (на 3 единицы ниже начальной точки).
Когда график касается оси X, объект находится на нулевой высоте (такой же, как его начальная высота). Это происходит в моменты времени t = 0 и t = 2,9.0003
Пример отрицательного смещения
Одним из наиболее распространенных примеров отрицательного смещения является падение объекта под действием силы тяжести.
Если вы уроните предмет из состояния покоя, он упадет на землю под действием силы тяжести. Если начальное положение — «нулевая» высота, то по мере падения высота объекта становится более отрицательной.
Это приводит к отрицательному смещению.
Ниже вы можете увидеть график отрицательного смещения падающего объекта.
Смещение падающего объекта под действием силы тяжести начинается с нуля и становится более отрицательным с течением времени. Обратите внимание, что с течением времени объект падает быстрее, поскольку ускорение силы тяжести имеет кумулятивный эффект на скорость.Заключение
Теперь вы знаете больше об отрицательном смещении, что оно означает и как оно может происходить. Вы также знаете, как скорость связана с перемещением.
Вы также знаете, как скорость связана с перемещением.
Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.
Вы также можете узнать об отрицательной скорости в моей статье здесь и об отрицательном ускорении в моей статье здесь.
Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!
Подпишитесь на наш канал на YouTube!
~Джонатон
Лекция 5: Перемещения
Дельта-обозначение
Когда я спрашиваю вас, который час, я действительно прошу вас дать мне показания часов. Однако, когда я спрашиваю, сколько времени занимает какое-то событие, я хочу знать интервал времени. Это два значения, в которых мы используем время. В физике обычно имеется в виду временной интервал вместо показаний часов. На самом деле время на часах действительно интервал времени от полуночи прошлой ночи. Чтобы математически различать интервал и показания часов мы используем так называемую «дельта-обозначение».Давайте рассмотрим два показания часов, например показания в начале и в конце гонки. Использовать буква t с нижними индексами 1 и 2 для обозначения первого и второго чтения соответственно. Интервал времени обозначается большой греческой дельтой, Δ, перед t , например это: Δ t = t 2 − t 1 Δ не означает «умножить на Δ». Это просто префикс, указывающий на изменение в количестве т . Для мирских событий, которые мы будем обсуждать, время всегда идет вперед и Δ t всегда положительно.Дельта-обозначение может использоваться для любой изменяющейся величины. В частности, положение может изменять. И, в отличие от времени, оно может изменяться в обе стороны, поэтому Δ
x может быть либо положительное или отрицательное. Система координат
Чтобы иметь возможность говорить о положении чего-либо, мы должны установить система координат, она же система отсчета. Ограничимся описанием что-то движется взад и вперед по одной линии.У нас будет достаточно проблем в одном измерение, прежде чем мы перейдем к двух- и трехмерному движению.
Рабочий объем
Позиция объекта определяется его положением на числовой прямой. Когда объект перемещается в другая позиция, его смещения — это вторая позиция минус первая позиция. Δ x = x 2 − x 1 Слово перемещение означает, что мы отслеживаем, каким образом происходит движение. В одной размер направление обозначается знаком: отрицательное, если влево, и положительное, если в право. Слово расстояние означает, как далеко перемещается объект независимо от направления. Это всегда положительна и равна абсолютному значению или величине смещения.Если следовать правилу всегда вычитать первую позицию из второй, знак всегда получается положительным, если смещение вправо, и отрицательным, если смещение происходит влево. (Это предполагает систему отсчета с положительной стороной ось справа).
Когда мы иллюстрируем смещение, рисуя стрелку с его хвост в первой позиции и кончик стрелы во второй, он будет указывать вправо для положительного смещения и влево для отрицательного смещения. Когда смещения происходят на отрицательной стороне оси, легко сделать ошибку с двойным знаком минус. Когда вы вычисляете смещения, вы следует сначала нарисовать стрелку, затем вычислить значение и, наконец, проверить, что знак совпадает с направлением стрелки.
Перемещение и расстояние, в чем разница?
Мы очень точно определили смещение. В этом определении знак очень важно. Путешествие из положения +3 в -3 представляет собой перемещение на −6 м. Обратный путь от −3 до +3 имеет водоизмещение +6 м. Полное водоизмещение для этой поездки можно добавить два смещения: (-6 м) + (+6 м) = 0 м. Общее расстояние, пройденное за все поездка не нулевая, это 12 м.Таким образом, слова расстояние и перемещение имеют очень разные значения, поскольку мы используем их в физике.
Небольшие прогулки
Вот несколько примеров смещения:Здесь у нас есть положительное смещение, происходящее на положительной стороне оси. начало и конец находятся на положительной стороне оси, начальное положение меньше, чем финиш. Следовательно, смещение положительное.
Когда конец ближе к началу координат и оба находятся на положительной стороне оси, тогда смещение отрицательное. Стрелка указывает влево, смещение отрицательное и все в порядке с миром.
Смещение к началу координат на отрицательной стороне оси положительно. Вычитание -4 от -1 дает положительный +3. Стрелка указывает вправо, поэтому знак правильный.
Движение влево должно давать отрицательное смещение даже на отрицательной стороне источник. Вычитание -2,5 из -4 дает -1,5. Хороший!
Вычисление перемещений, которые пересекают начало координат, может оказаться сложной задачей.Но направление г. стрелка всегда дает правильный знак. Вот два последних примера.
Знак смещения не зависит от того, где происходит смещение, но только по своему направлению. В самом деле, если бы числовая линия была смещена влево или вправо, все измерения положения были бы другими, но смещения не изменились бы.
Движение, происходящее вперед и назад по числовой прямой, можно представить график положение-время. Горизонтальное измерение графика представляет время, со временем течет слева направо. Числовая линия представлена вертикальным размером график с положительными позициями над осью времени и отрицательными позициями под ней.Совершите небольшое путешествие…
Давайте отправимся в путешествие и покажем, как это будет выглядеть на графике положение-время. я катаюсь наNinja Kawasaki Power-Wheels с двумя скоростями вперед и одной назад. я начинаю из положения −5 в высокий, затем переключиться в низкий и через несколько секунд с визгом остановиться. Включив задний ход, я возвращаюсь к началу, останавливаюсь и выхожу. Вот что может выглядеть графическое представление этой поездки.
В течение первых двух секунд я разгоняюсь до высокой скорости. Скорость определяется как изменение положения, деленное на интервал времени, в течение которого произошло это изменение:Судя по графику, скорость довольно постоянна от второй до четвертой второй. Между 2,5 и 3,5 с Δ x составляет около 2,57 м. Δ t составляет 1 с. Таким образом, v = 2,57 м/1с. = 2,57 м/с в области высоких скоростей. Слово скорость обычно используется для обозначения абсолютного значения скорости. Скорость может быть отрицательным, когда он движется к отрицательной стороне оси. Скорость будет положительный в таком случае. Другими словами, скорость равна пройденному пути, деленному на время интервал.
[ Различие между скоростью и скоростью, расстоянием и смещение полезно, но используемые слова произвольны.я попробую используйте эти слова последовательно, как я определил их в этих лекциях. Ты однако следует отметить, что иногда другие авторы могут быть не совсем такими последовательный. В частности, первое издание PSSC Physics в нашей библиотеке использует скорость в одномерном случае означает смещение, деленное на время интервал, то есть наша скорость. Во втором и более поздних изданиях используется термин так же, как и мы.]
После нажатия кнопки низкой скорости тележка замедляется или замедляется. Мы используем слово «ускорение» для этого замедления тоже. Когда тележка движется в плюс направлении, замедление будет технически называться ускорением, которое является отрицательным. Между t = 5,5 с и t = 8,5 с скорость относительно постоянна. Как видите, в течение 1 с интервалом в этом районе тележка прошла 0,85 с. Таким образом, скорость здесь равна 0,85 м/с.При остановке тележка снова ускоряется отрицательно. Другими словами, тележка теряет часть своей положительной скорости, пока не достигнет нуля.

 Иксi < 0, хf = 0
Иксi < 0, хf = 0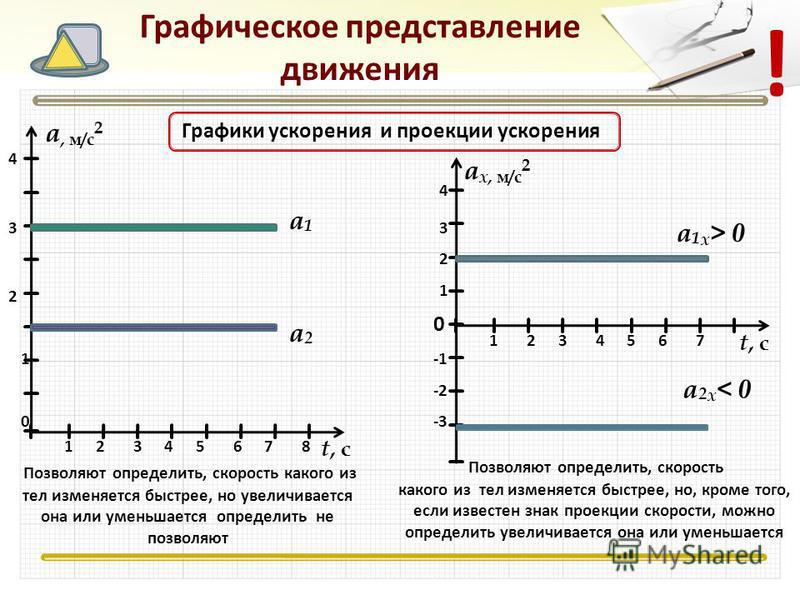 Смещение этой частицы является примером положительного смещения.
Смещение этой частицы является примером положительного смещения. Он начал двигаться из точки A вдоль отрицательной оси y. Точка A находится на расстоянии 5 м по отрицательной оси y. После этого эта частица достигла точки, лежащей вдоль положительной оси у на расстоянии 5 м. затем снова частица переместилась в точку С, расположенную по отрицательной оси у на расстоянии 5 м, а оттуда частица переместилась в точку D, расположенную по положительной оси у на расстоянии 5 м. затем снова эта частица переместилась в точку E вдоль отрицательной оси y на расстояние 5 м и, наконец, достигла точки F. каково будет ее полное перемещение?
Он начал двигаться из точки A вдоль отрицательной оси y. Точка A находится на расстоянии 5 м по отрицательной оси y. После этого эта частица достигла точки, лежащей вдоль положительной оси у на расстоянии 5 м. затем снова частица переместилась в точку С, расположенную по отрицательной оси у на расстоянии 5 м, а оттуда частица переместилась в точку D, расположенную по положительной оси у на расстоянии 5 м. затем снова эта частица переместилась в точку E вдоль отрицательной оси y на расстояние 5 м и, наконец, достигла точки F. каково будет ее полное перемещение?
 У нас будет достаточно проблем в одном
измерение, прежде чем мы перейдем к двух- и трехмерному движению.
У нас будет достаточно проблем в одном
измерение, прежде чем мы перейдем к двух- и трехмерному движению.

 Но направление г.
стрелка всегда дает правильный знак. Вот два последних примера.
Но направление г.
стрелка всегда дает правильный знак. Вот два последних примера.  Включив задний ход, я возвращаюсь к началу, останавливаюсь и выхожу. Вот что
может выглядеть графическое представление этой поездки.
Включив задний ход, я возвращаюсь к началу, останавливаюсь и выхожу. Вот что
может выглядеть графическое представление этой поездки.  я попробую
используйте эти слова последовательно, как я определил их в этих лекциях. Ты
однако следует отметить, что иногда другие авторы могут быть не совсем такими
последовательный. В частности, первое издание PSSC Physics в нашей библиотеке использует
скорость в одномерном случае означает смещение, деленное на время
интервал, то есть наша скорость. Во втором и более поздних изданиях используется термин
так же, как и мы.]
я попробую
используйте эти слова последовательно, как я определил их в этих лекциях. Ты
однако следует отметить, что иногда другие авторы могут быть не совсем такими
последовательный. В частности, первое издание PSSC Physics в нашей библиотеке использует
скорость в одномерном случае означает смещение, деленное на время
интервал, то есть наша скорость. Во втором и более поздних изданиях используется термин
так же, как и мы.]
Leave A Comment