Подготовка к ГИА. Реальная математика. Часы
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Подготовка к ГИА. Реальная математика.
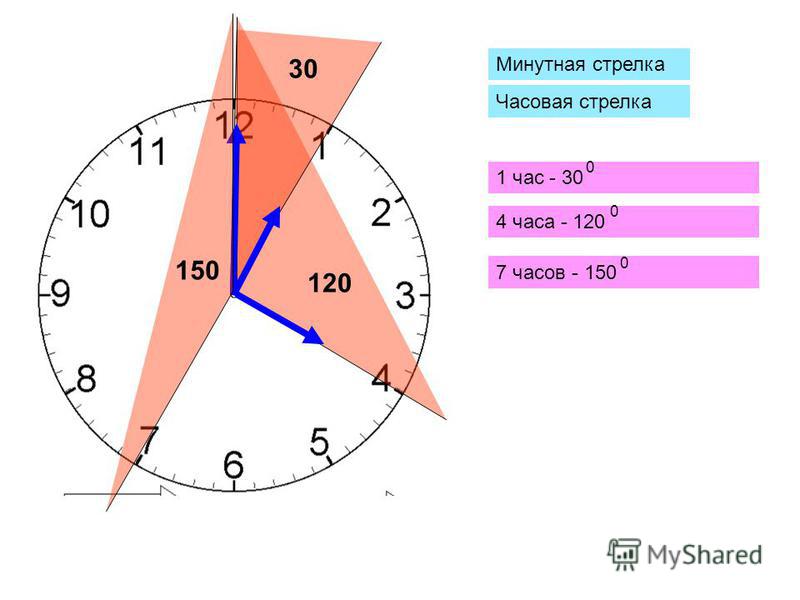
ЧАСЫ.30
Минутная стрелка
Часовая стрелка
1 час — 30
0
4 часа — 120
150
120
0
7 часов — 150
0
3. Какой угол образуют минутная и часовая стрелки в 2 часа?
1260
15
120
4. Какой угол образуют минутная и часовая стрелки в 10 часов?
120340
60
240
5.
Какой угол образуют минутная и часовая стрелки в 6 часов?36090
36
180
6. Какой угол образуют минутная и часовая стрелки в 16 часов 30 минут?
9015
45
120
7. Какой угол образуют минутная и часовая стрелки в 11 часов 30 минут?
185165
15
120
6
Минутная стрелка
30
60
за один час делает полный
0
оборот — 360
за одну минуту делает 1/60
0
часть оборота — 6
за 5 минут — 6*5 = 300
за 10 минут — 6*10 = 600
0
за n минут — 6*n = 6n
9. Какой угол описывает минутная стрелка за 30 минут?
18090
60
5
10. Какой угол описывает минутная стрелка за 11 минут?
3366
11
55
11. Какой угол описывает минутная стрелка за 3 минуты?
2115
18
12
12. Какой угол описывает минутная стрелка за 40 минут?
60240
40
220
13. Какой угол описывает минутная стрелка за 1 час 7 минут?
42678
367
402
Часовая стрелка
30
0
за один час — 30
60
за 2 часа — 30*2 = 60 0
за 5 часов — 30*5 = 1500
0
за n часов — 30*n = 30n
150
за одну минуту — 1/60 от
0
часа, т.
е. от 30 30 : 60 = 0,50
за 5 минут 0,5*5=2,5 0
за 20 минут 0,5*20=10 0
за n минут 0,5*n=0,5n 0
Какой угол описывает часовая
стрелка за 4 часа?
120
24
2
140
Какой угол описывает часовая
стрелка за 8 часов?
40
120
4
240
17. Какой угол описывает часовая стрелка за 4 часа?
Какой угол описывает часоваястрелка за 7 часов?
42
3,5
210
120
18. Какой угол описывает часовая стрелка за 8 часов?
Какой угол описывает часоваястрелка за 15 минут?
90
450
7,5
75
19. Какой угол описывает часовая стрелка за 7 часов?
Какой угол описывает часоваястрелка за 42 минуты?
84
252
42
21
20. Какой угол описывает часовая стрелка за 15 минут?
Комбинированныезадачи
21. Какой угол описывает часовая стрелка за 42 минуты?
Какой угол описывает часоваястрелка за 5 часов 52 минуты?
176
552
146
76
Какой угол описывает часовая
стрелка за 3 часа 6 минут?
36
93
96
186
23.
Какой угол описывает часовая стрелка за 5 часов 52 минуты?Какой угол описывает часоваястрелка за 1 час 50 минут?
176
55
146
76
24. Какой угол описывает часовая стрелка за 3 часа 6 минут?
Какой угол описывает часоваястрелка за 10 часов 10 минуты?
305
185
315
365
25. Какой угол описывает часовая стрелка за 1 час 50 минут?
Какой угол описывает часоваястрелка за 8 часов 20 минуты?
140
260
250
130
26. Какой угол описывает часовая стрелка за 10 часов 10 минуты?
Совсемкомбинированные
задачи
27. Какой угол описывает часовая стрелка за 8 часов 20 минуты?
На какой угол поворачиваетсяминутная стрелка, пока часовая
проходит 0,5 градусов?
2
6
4
30
На какой угол поворачивается
минутная стрелка, пока часовая
проходит 10 градусов?
120
4
20
240
29. На какой угол поворачивается минутная стрелка, пока часовая проходит 0,5 градусов?
На какой угол поворачиваетсяминутная стрелка, пока часовая
проходит 18 градусов?
6
18
216
36
30.
На какой угол поворачивается минутная стрелка, пока часовая проходит 10 градусов?На какой угол поворачиваетсячасовая стрелка, пока минутная
проходит 30 градусов?
2,5
5
360
7,5
31. На какой угол поворачивается минутная стрелка, пока часовая проходит 18 градусов?
На какой угол поворачиваетсячасовая стрелка, пока минутная
проходит 240 градусов?
120
160
20
40
English Русский Правила
Задачи со стрелками исправных часов
Попробуйте решить самостоятельно!
Если что-то не получается, не отчаивайтесь, ответ и решение расположены ниже.
1. Сколько раз в сутки показания часов обладают тем свойством, что, меняя местами минутную и часовую стрелки, мы придем к имеющему смысл показанию часов?
2.
Сколько раз в сутки часовая и минутная стрелки образуют прямой угол?
3.
Через сколько минут стрелки часов (нормальных) после совмещения наложатся снова?
4.
5.
Сколько раз часовые стрелки будут находится одна над другой в течение 12 часов?
6.
Некоторая работа была начата в пятом часу, а закончена в восьмом часу, причем показания часов в начале и в конце работы переводятся друг в друга, если поменять местами часовую и минутную стрелки. Определить продолжительность работы и показать, что в начале и в конце работы стрелки были одинаково отклонены от вертикального направления.
7.
Сколько раз в сутки минутная стрелка обгоняет часовую? А секундная?
8.
Часы пробили полночь. Сколько раз и в какие моменты времени до следующей полуночи часовая и минутная стрелки будут совмещены?
9.
Между какими цифрами находится секундная стрелка в момент первого совмещения часовой стрелки с минутной после полудня?
10.
Почему на часах стрелки ходят слева направо (по часовой стрелке), а не наоборот?
11. На часах с тремя стрелками — часовой, минутной и секундной — в 12 часов все три стрелки совпадают. Существуют ли еще другие моменты времени, когда все три стрелки совпадают?
12.
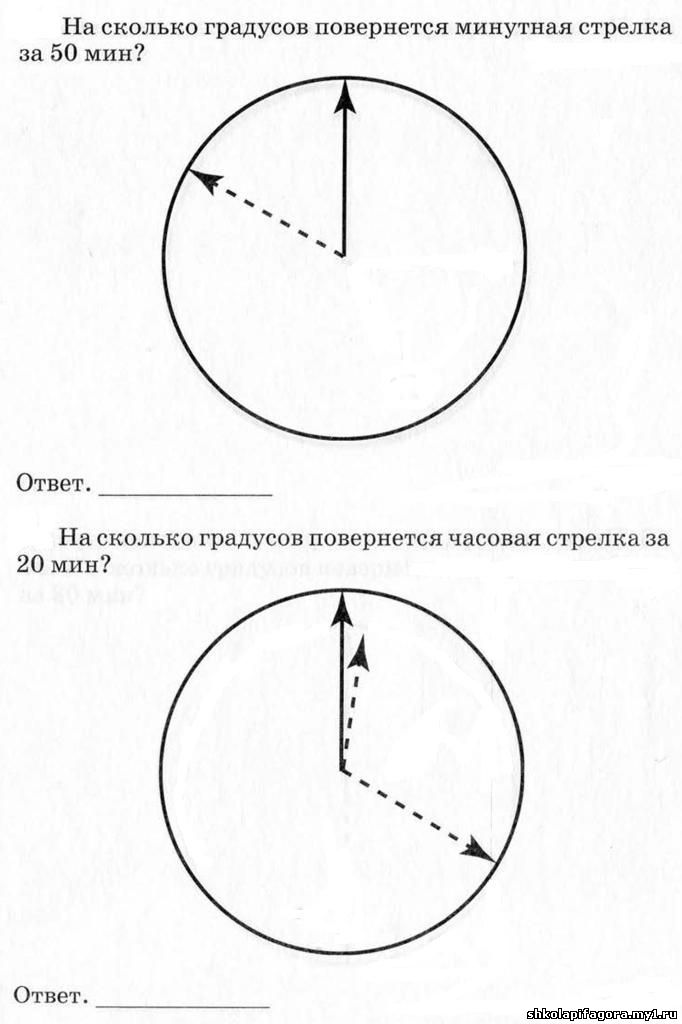
13. На сколько градусов поворачивается за минуту минутная стрелка? Часовая стрелка?
14.
Определите величину угла между часовой и минутной стрелками часов, показывающими 1 час 10 минут при условии, что обе стрелки движутся с постоянными скоростями.
15. Стрелки часов только что сошлись. Через сколько минут они будут «смотреть» в противоположные стороны?
17.
Когда
же произойдет следующая встреча?
18.
В 6 часов, наоборот, обе стрелки направлены в противоположные стороны. Но только ли в 6 часов это бывает или же есть и другие моменты, когда стрелки так расположены?
19.
Я взглянул на часы и заметил, что обе стрелки отстоят от цифры 6, по обе ее стороны, одинаково. В котором часу это было?
20.
В котором часу минутная стрелка опережает часовую ровно на столько же, на сколько часовая находится впереди числа 12 на циферблате? А может быть, таких моментов бывает в день несколько или же вовсе не бывает?
21. Какой угол образуют стрелки часов в 12 часов 20 минут?
22. Найдите угол между часовой и минутной стрелками а) в 9 часов 15 минут; б) в 14 часов 12 минут?
23.
Когда
угол между часовой и минутной стрелками часов больше а) в 13:45 или в
22:15; б) в 13:43 или в 22:17; в) через t минут после полудня
или за t минут до полуночи?
24. Стрелки часов только что сошлись. Через сколько минут они будут «смотреть» в противоположные стороны?
25. Как можно объяснить, что в исправных часах за одну секунду минутная стрелка прошла 6 минут.
27. В
Италии выпускают часы, в которых часовая стрелка делает в сутки один оборот, а
минутная – 24 оборота, причём, как обычно, минутная стрелка длиннее
часовой (в обычных часах часовая стрелка делает в сутки два оборота, а
минутная – 24).
Рассмотрим все положения двух стрелок и нулевого деления,
которые встречаются и на итальянских часах, и на обычных. Сколько существует
таких положений? (Нулевое деление отмечает 24 часа в итальянских часах и 12
часов в обычных часах).
28. Вася измерил транспортиром и записал в тетрадку углы между часовой и минутной стрелками сначала в 8:20, а потом в 9:25. После этого Петя забрал свой транспортир. Помогите Васе найти углы между стрелками в 10:30 и 11:35.
29. Сколько раз с 12:00 до 23:59 совпадают минутная и часовая стрелки часов?
30. На часах полдень. Когда часовая и минутная стрелки совпадут в следующий раз?
32.
Когда
Петя начал решать эту задачу, он заметил, что часовая и минутная стрелки его
часов образуют прямой угол. Пока он решал ее, угол все время был тупым, а в тот
момент, когда Петя закончил решение, угол снова стал прямым. Сколько времени
Петя решал эту задачу?
33. Петя проснулся в восьмом часу утра и заметил, что часовая стрелка его будильника делит пополам угол между минутной стрелкой и стрелкой звонка, показывающей на цифру 8. Через какое время должен прозвенеть будильник?
34. Коля отправился за грибами между восемью и девятью часами утра в момент, когда часовая и минутная стрелки его часов были совмещены. Домой он вернулся между двумя и тремя часами дня, при этом стрелки его часов были направлены в противоположные стороны. Сколько продолжалась Колина прогулка?
35. Ученик
начал решать задачу между 9 и 10 часами и закончил между 12 и 13 часами.
Сколько времени он решал задачу, если за это время часовая и минутная стрелки
часов поменялись местами?
36. Сколько раз в течение суток часовая и минутная стрелки правильно идущих часов образуют угол в 30 градусов?
37. Перед вами часы. Сколько существует положений стрелок, по которым нельзя определить время, если не знать, какая стрелка часовая, а какая минутная? (Считается, что положение каждой из стрелок можно определить точно, но следить за тем, как стрелки двигаются, нельзя.)
38. В мире антиподов минутная стрелка часов идет с нормальной скоростью, но в противоположную сторону. Сколько раз за сутки стрелки антиподных часов а) совпадают; б) противоположны?
39. Сколько раз в сутки антиподные часы невозможно отличить от нормальных (если не знать, который час на самом деле)?
40.
Муха в полдень села на секундную стрелку часов и
поехала, придерживаясь следующих правил: если она обгоняет какую-то стрелку или
ее обгоняет какая-то стрелка (кроме секундной у часов есть часовая и минутная
стрелки), то муха переползает на эту стрелку. Сколько кругов проедет муха
в течение часа?
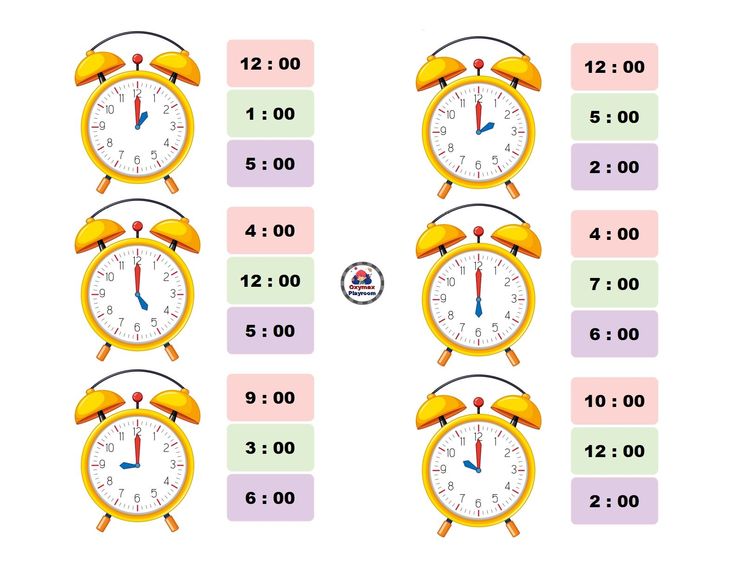
Выяснить закономерность в изменении времени на часах и определить, что должны показывать часы под номером пять.
Ответ
Закономерность: На втором циферблате к первому плюс 2 часа 10 минут, На третьем циферблате ко второму минус 3 часа 20 минута, на четвертом циферблате к третьему плюс 4 часа 30 минут. Следовательно, разница между показаниями циферблата 5 и 4 будет минус 5 часов 40 минут.
Задания с ОГЭ
1. Какой угол (в градусах) образуют минутная и часовая
стрелки часов в 4 ч?
2.
Какой угол (в градусах) описывает
минутная стрелка за 6 минут?
Задания ЕГЭ
1. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
Эта задача ничуть не сложнее, чем задача на движение по кругу. У нас по кругу движутся часовая и минутная стрелки. Минутная стрелка за час проходит полный круг, то есть 360°. Значит, ее скорость равна 360° в час. Часовая стрелка за час проходит угол 30° ( это угол между двумя соседними числами на циферблате). Значит, ее скорость 30° в час.
В 8 часов 00 минут расстояние между стрелками составляет 240°:
Пусть минутная стрелка в первый раз встретится с часовой через t часов. За это время минутная стрелка пройдет 360°t, а часовая 30°t, причем минутная пройдет на 240° больше, чем часовая. Получим уравнение:
360°t-30°t=240°
t=240°/330°=8/11
То есть через 8/11 часа стрелки первый раз встретятся.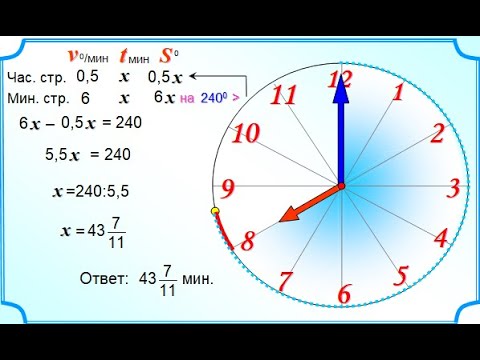
Теперь до следующей встречи минутная стрелка пройдет на 360° больше, чем часовая. Пусть это произойдет через х часов.
Получим уравнение:
360°х-30°х=360°. Отсюда х=12/11. И так еще два раза.
Получаем, что минутная стрелка в четвертый раз поравняется с часовой через 8/11+12/11+12/11+12/11= 4 часа= 240 мин.
Ответ: 240 мин.
2. Часы со стрелками показывают 1 час 35 минут. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?
В этой задаче скорость движения стрелок будем выражать в градусах/минуту.
Скорость минутной стрелки равна 360˚/60=6˚ в минуту.
Скорость часовой стрелки равна 30˚/60=0,5˚ в минуту.
В 0 часов положение часовой и минутной стрелок совпадало. 1 час 35 минут — это 95 минут. За это время минутная стрелка прошла 95х6=570˚=360˚+210˚, а часовая прошла 95×0,5˚=47,5˚. И у нас такая картинка:
Первый раз стрелки встретятся через время , когда часовая стрелка повернется на , а минутная на 150˚+47,5˚ больше.
Получаем уравнение для :
Отсюда
Следующий раз стрелки встретятся, когда минутная пройдет на круг больше часовой:
И так 9 раз.
Минутная стрелка в десятый раз поравняется с часовой через минут
Ответ: 625
Ответы:
1. за 12 часов 132, за 24 часа 264 момента плюс 22 наложения, итого 286
2. В сутки часовая стрелка делает 2 оборота , а минутная — 24 . Отсюда минутная стрелка обгоняет часовую 22 раза и каждый раз с часовой стрелкой образуется по два прямых угла, т.е. ответ — 44.
3.Нетрудно сообразить, что это случится спустя 1 час 5
5/11 минуты, то есть в 2 часа 10 10/11минуты. Следующая — спустя еще 1 час 5
5/11 минуты, то есть в 3 часа 16 4/11 минуты, и т.
д. Всех встреч, как легко
видеть, будет 11; 11-я наступит через 1 1/11 —12 часов после первой, то есть в
12 часов; другими словами, она совпадает с первой встречей, и дальнейшие
встречи повторятся снова в прежние моменты.
Вот все моменты встреч:
1-я встреча — в 1 час 5 5/11 минуты
2-я « — «2 часа 10 10/11 «
3-я « — «3 часа 16 4/11 «
4-я « — «4 часа 21 9/11 «
5-я « — «5 часов 27 3/11 «
6-я « — «6 часов 32 8/11 «
7-я « — «7 часов 38 2/11 «
8-я « — «8 часов 43 7/11 «
9-я « — «9 часов 49 1/11 «
10-я « — «10 часов 54 6/11 «
11-я « — «12 часов
через 65,(45) мин=65 9/11 мин.
4. в 5 раз
6. начало в 4 часа 36, 923 мин, конец в 7 часов 23, 076 мин, длительность 2 часа 46, 153 мин.
7. В сутки часовая стрелка делает 2 оборота, а минутная — 24 . Отсюда минутная стрелка обгоняет часовую 22 раза.
9. 4 и 5
10. Именно так движется тень в самых первых часах — солнечных. А затем уже механические часы скопировали направление движения стрелок. Кстати, в Южном полушарии все наоборот — тень в солнечных часах движется против часовой стрелки.
11. Не существует.
12. Кэрролл считал, что точными являются
стоящие часы. Вот как он это обосновывал. Часы, отстающие на минуту в сутки,
показывают точное время один раз в два года, в то время как стоящие часы
показывают точное время два раза в сутки.
13. За час минутная стрелка делает полный оборот. Значит, за минуту она поворачивается на1/60часть угла в 360°, то есть на 6°. Часовая стрелка за час проходит1/12часть круга, то есть движется в 12 раз медленнее минутной. За минуту она поворачивается на 0,5°.
14. В 1:00 минутная стрелка «отставала» от часовой на 30°. За 10 минут, прошедших после этого момента, часовая стрелка «пройдёт» 5°, а минутная – 60°, поэтому угол между ними равен 60° – 30° – 5° = 25°.
15. Пусть х − промежуток времени в минутах, который
должен пройти, прежде чем стрелки разместятся на одной прямой и будут
направлены в разные стороны. Минутная стрелка успеет пройти за это время х
минутных делений циферблата, а часовая — х/12 минутных делений. Когда
стрелки разместятся на одной прямой и будут направлены в разные стороны, их
будут разделять 30 минутных делений циферблата. А значит, в это время x –
x/12 = 30, откуда х = 32 (8/11).
Через 32 (8/11) минут стрелки будут
«смотреть» в противоположные стороны.
16. Начнем
наблюдать за движением стрелок в 12 часов. В этот момент обе стрелки друг друга
покрывают. Так как часовая стрелка движется в 12 раз медленнее, чем минутная
(она описывает полный круг в 12 часов, а минутная в 1 час), то в течение
ближайшего часа стрелки, конечно, встретиться не могут. Но вот прошел час;
часовая стрелка стоит у цифры 1, сделав 1/12 долю полного оборота; минутная же
сделала полный оборот и стоит снова у 12 — на 1/12 долю круга позади часовой.
Теперь условия состязания иные, чем раньше: часовая стрелка движется медленнее
минутной, но она впереди, и минутная должна ее догнать. Если бы состязание
длилось целый час, то за это время минутная стрелка прошла бы полный круг, а
часовая 1/12 круга, то есть минутная сделала бы на 11/12 круга больше. Но,
чтобы догнать часовую стрелку, минутной нужно пройти больше, чем часовой,
только на ту 1/12 долю круга, которая их отделяет.
Для этого потребуется
времени не целый час, а меньше во столько раз, во сколько раз 1/12 меньше
11/12, то есть в 11 раз. Значит, стрелки встретятся через 1/11 часа, то есть
через 60/11 = 5 5/11 минуты. Итак, встреча стрелок случится спустя 5 5/11
минуты после того, как пройдет 1 час, то есть в 5 5/11 минуты второго.
21. Ответ: Нетрудно сообразить, что это случится спустя 1 час 5 5/11 минуты, то есть в 2 часа 10 10/11минуты. Следующая — спустя еще 1 час 5 5/11 минуты, то есть в 3 часа 16 4/11 минуты, и т. д. Всех встреч, как легко видеть, будет 11; 11-я наступит через 1 1/11 —12 часов после первой, то есть в 12 часов; другими словами, она совпадает с первой встречей, и дальнейшие встречи повторятся снова в прежние моменты.Вот все моменты встреч:
24. Пусть обе стрелки стояли у 12, и затем часовая
отошла от 12 на некоторую часть полного оборота, которую мы обозначим буквой х.
Минутная стрелка за то же время успела повернуться на 12х. Если времени
прошло не больше одного часа, то для удовлетворения требования нашей задачи
необходимо, чтобы минутная стрелка отстояла от конца целого круга на столько
же, на сколько часовая стрелка успела отойти от начала; другими словами: 1 — 12
• х = х Отсюда 1 = 13 • х. Следовательно, х = 1/13 доле целого оборота. Такую
долю оборота часовая стрелка проходит в 12/13 часа, то есть показывает 55 5/13
минуты первого. Минутная стрелка в то же время прошла в 12 раз больше, то есть
12/13 полного оборота; обе стрелки, как видите, отстоят от 12 одинаково, а
следовательно, одинаково отодвинуты и от 6 по разные стороны. Мы нашли
одно положение стрелок — именно то, которое наступает в течение первого часа. В
течение второго часа подобное положение наступит еще раз; мы найдем его,
рассуждая по предыдущему, из равенства 1— (12х — 1) = х, или 2— 12х = х, откуда
2 = 13х, и , следовательно, х = 2/13 полного оборота. В таком положении стрелки
будут в 1 11/13 часа, то есть в 50 10/13 минуты второго.
В третий раз стрелки
займут требуемое положение, когда часовая стрелка отойдет от 12 на 3/13 полного
круга, то есть 2 10/13 часа, и т. д. Всех положений 11, причем после 6 часов
стрелки меняются местами: часовая стрелка занимает те места, в которых была
раньше минутная, а минутная становится на места часовой.Если вы внимательно
наблюдаете за часами, то, быть может, вам случалось наблюдать и как раз
обратное расположение стрелок, чем сейчас описано: часовая стрелка опережает
минутную на столько же, на сколько минутная продвинулась вперед от числа 12.
Когда же это бывает? Ответ: В первый раз требуемое расположение стрелок будет в
тот момент, который определяется равенством:12х — 1 = х/2, откуда 1 = 11 ½ х,
или х = 2/23 целого оборота, то есть через 1 1/23 часа после 12. Значит, в 1
час 21 4/23 минуты стрелки будут расположены требуемым образом. Действительно,
минутная стрелка должна стоять посередине между 12 и 1 1/23 часами, то есть на
12/23 часа, что как раз и составляет 1/23 полного оборота (часовая стрелка
пройдет 2/23 целого оборота).
Второй раз стрелки расположатся
требуемым образом в момент, который определится из равенства: 12х —
2= х/2, откуда 2 = 11 1/2 х и х = 4/23; искомый момент — 2 часа 5 5/23
минуты.Третий искомый момент — 3 часа 7 19/23 минуты, и т. д.
40. 21 круг
Калькулятор угла часов | Найдите угол между стрелками часов. Математическая задача с часами
Калькулятор угла часов поможет вам решить некоторые распространенные математические задачи часов, например, ‘ Как найти угол часовых стрелок, зная время? ‘ Это то время, когда вы начинаете изучать углы в школе? Или, может быть, вам нравится решать математические задачи для развлечения, и вы не уверены, есть ли у вас правильный ответ? ⏰
Продолжайте читать, чтобы узнать:
- Сколько двигаются стрелки аналоговых часов каждый час и минуту;
- Как найти угол между стрелками часов, руководствуясь только здравым смыслом;
- Как найти угол по формулам угла часов; и
- Почему вы всегда должны визуализировать математические задачи с часами.
Наш блестящий калькулятор угла часов поможет вам со всеми вашими потребностями угла часов. Итак, приступим! Нет свободного времени.
Углы часов 🕓 — угол между стрелками часов
Посмотрите на аналоговые часы. Более короткая часовая стрелка делает полный оборот за 12 часов. Это означает, что каждый час он перемещается на 30 градусов .
360° / 12 = 30°
Но часовая стрелка не движется каждый час! Каждую минуту он перемещается на полградуса .
30° / 60 = 0,5°
Минутная стрелка делает полный оборот за 60 минут. Итак, каждую минуту перемещается на 6 градусов.
360° / 60 = 6°
Чтобы найти углы, создаваемые стрелками часов, вы можете использовать два метода :
Первый способ для тех, кто предпочитает приходить к решению логически и без всяких формул.
Второй способ для тех, кто любит пользоваться формулами.
Как вы знаете, у компьютеров нет здравого смысла, поэтому наш калькулятор часового угла работает благодаря формулам. Поскольку вы, вероятно, не компьютер, не стесняйтесь использовать метод, который вам более удобен.
Метод 1 – простая математическая задача с часами
Найти угол между часовой и минутной стрелками легко, когда на часах есть полный час . Минутная стрелка нацелена на число 12, поэтому угол равен часу, умноженному на 30 градусов !
🙋 Первое, что вы должны сделать после прочтения математической задачи с часами, это визуализировать! Создайте простой рисунок с заданным временем. ⏰
Итак, давайте попробуем это на примере:
Пример 1. Какой угол между стрелками часов в 4 часа?
Угол между стрелками часов = 30° * 4 = 120°
Искомый угол составляет 120 градусов. Но знаете ли вы, что есть два угла между стрелками аналоговых часов? Второй заполняет пространство по другую сторону часовой и минутной стрелок.
Вы можете найти его, вычитая один угол из полного оборота (360°):
360° - 120° = 240°
Наш калькулятор часового угла даст вам два угла, расширенных по часовой стрелке:
- Угол от часовая минутная стрелка , в данном примере –
240°; и - Угол между минутной и часовой стрелками , здесь –
120°.
🔎 Вы также можете рассчитать длину дуги, которую создают стрелки часов. Узнайте, как это сделать, в калькуляторе длины дуги.
Метод 1 – более сложная математическая задача с часами
Теперь давайте посмотрим, как найти угол между стрелками часов без использования каких-либо формул в более сложной математической задаче с часами:
Пример 2. Время на аналоговых часах показывает 10 :14. Какой угол между стрелками часов?
Сначала нарисуйте часы и отметьте характерные части ракурса.
Мы начали с обозначения угла b , так как проще всего найти его размер.
Он содержит 3 полных часа (от числа 11 до числа 2), поэтому он равен:
b = 3 * 30° = 90°
Затем мы отметили два оставшихся места с a (рядом с часовой стрелкой). ) и c (рядом с минутной стрелкой).
Сначала найдем . Мы видим на изображении, что он меньше 30°. Самый простой способ найти a , чтобы увидеть, как далеко часовая стрелка находится от числа 10. Угол между часовой стрелкой и числом 10 на часах составляет 14 минут, умноженных на 0,5°.
14 * 0,5° = 7°
Итак, как далеко часовая стрелка от цифры 11?
a = 30° - 14 * 0,5° = 30° - 7° = 23°
Наконец, мы должны найти угол c . Минутная стрелка перемещается между цифрой два туда, где она сейчас находится через четыре минуты. Мы уже знаем, что он также перемещается на 6° каждую минуту. Итак, c равно:
c = 4 * 6° = 24°
Угол между часовой и минутной стрелками равен:
Угол между стрелками часов = 90° + 23° + 24° = 137°
Помните — есть два угла часов! Другой:
360° - 137° = 223°
Способ 2 – используйте формулу угла часов
Как найти угол часовых стрелок в более сложном примере?
Снова начните с рисования часов.
Отметьте угол между минутной стрелкой и 12 часами. Мы уже знаем, что минутная стрелка перемещается на 6° каждую минуту. Таким образом, чтобы вычислить угол между минутной стрелкой и 12 часами , умножьте количество минут на 6 градусов.
Угол мин = 6° x количество минут
Теперь отметьте угол между часовой стрелкой и 12 часами. Помните, что часовая стрелка движется каждую минуту. Итак, чтобы найти правильный угол, мы также должны учитывать количество минут. Итак, Формула угла часов для часовой стрелки :
Угол часа = 30° x количество часов + 0,5° x количество минут ,
, потому что часовая стрелка перемещается на 30° каждый полный час, а затем на 0,5° каждую минуту.
Наконец, найдите два угла часов. Чтобы найти первый, вычтите меньший угол из большего. Другими словами, найдите абсолютное значение разности двух углов:
Первый угол между стрелками часов = |Угол 902:02 часов — Угол минут |
Воспользуемся этими инструкциями и решим математическую задачу с часами:
Пример 3.
Найдите угол между стрелками часов в 8:23.
Наконец, вычтите значения:
Угол часовой стрелки больше угла минутной стрелки, поэтому:
Угол ч — Угол мин = 251,5° — 138° = 113,5° .
Первый угол между стрелками часов равен 113,5°.
Если нужно, найдите второй угол:
360° — Первый угол между стрелками часов = 360° — 113,5° = 246,5°
Теперь выберите свой любимый метод и решите все математические задачи с часами! И помните — вы всегда можете проверить свой ответ в нашем калькуляторе угла часов ! Прежде чем вы пойдете, в калькуляторе преобразования углов вы можете узнать, как конвертировать между различными единицами для описания углов.
Юлия Жулавиньская
Введите время с аналоговых часов:
Минуты
Угол от часовой до минутной стрелки
Угол от минутной до часовой стрелки
Посмотрите 6 подобных калькуляторов углов 🕑
Угол между двумя векторами Центральный угол Дополнительные углы…
Часы сломаны.
Но его часовая, минутная и секундная стрелки по-прежнему движутся с постоянной скоростью в нормальном направлении. Секундная стрелка проходит через часовую каждые 10 секунд (m ) РЕШЕНИЕ: Часы сломаны. Но их часовая, минутная и секундная стрелки все еще движутся.
с постоянными скоростями в нормальном направлении. Секундная стрелка проходит часовую стрелку
каждые 10 секунд (мАлгебра -> Настраиваемые средства решения задач Word -> Разное -> РЕШЕНИЕ: Часы сломаны. Но его часовая стрелка, минутная стрелка и секундная стрелка все еще движутся с постоянными скоростями в нормальном направлении. Секундная стрелка проходит часовую стрелку каждые 10 секунд (м Войти
|
Но его часовая, минутная и секундная стрелки по-прежнему движутся на 90 297 с постоянной скоростью в нормальном направлении. Секундная стрелка проходит часовую стрелку 
Leave A Comment