3. Площади
1. Найдите площадь ромба, стороны которого равны 5, а высота равна 4.
2. Найдите сторону квадрата, площадь которого равна сумме площадей квадратов со сторонами 5 и 12.
3. Даны два квадрата, стороны которых равны 10 и 8. Найдите сторону квадрата, площадь которого равна разности площадей данных квадратов.
4. Найдите площадь параллелограмма, если его стороны равны 2 и 4, а один из углов равен 150°.
5. Найдите площадь параллелограмма, если две его стороны равны 8 и 10, а угол между ними равен 30°.
6. Найдите площадь параллелограмма, если две его стороны равны 4 и 6, а угол между ними равен 60°.
7. Найдите площадь ромба, если его высота равна 2, а острый угол равен 45о.
8.
Стороны параллелограмма равны 9 и 15.
Высота, опущенная на меньшую сторону,
равна 10. Найдите высоту, опущенную на
большую сторону параллелограмма.
9. Найдите площадь прямоугольника, если его периметр равен 18 и одна сторона на 3 больше другой.
10. Площадь прямоугольника равна 18. Найдите его большую сторону, если она в два раза больше меньшей стороны.
11. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту параллелограмма.
12. Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь треугольника.
13. Найдите площадь прямоугольника, сторона которого равна 6, а диагональ равна 10.
14. Найдите площадь квадрата, если его диагональ равна 8.
15. Найдите площадь ромба, если его диагонали равны 4 и 12.
16. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
17. Площадь ромба
равна 6. Одна из его диагоналей в 3 раза
больше другой. Найдите меньшую диагональ.
18. Площадь ромба равна 16. Одна из его диагоналей в 2 раза меньше другой. Найдите большую диагональ.
19. Площадь квадрата равна 12. Найдите площадь квадрата, вершинами которого являются середины сторон данного квадрата.
21. Площадь параллелограмма ABCD равна 10. Найдите площадь параллелограмма A’B’C’D’, вершинами которого являются середины сторон данного параллелограмма.
22. Площадь квадрата ABCD, описанного около окружности, равна 36. Найдите площадь квадрата, вписанного в эту окружность.
23. Площадь прямоугольника равна 12. Найдите площадь ромба, вершинами которого являются середины сторон данного прямоугольника.
25. Стороны ромба равны 6, а его площадь равна 24. Найдите радиус вписанной окружности.
26. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.
27. Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь треугольника.
28. Площадь равнобедренного треугольника равна 48, а основание равно 16. Найдите боковую сторону треугольника.
29. Найдите площадь треугольника, две стороны которого равны 3 и 4, а угол между ними равен 60°.
30. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 10. Найдите площадь треугольника.
31. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150°. Найдите боковую сторону треугольника, если его площадь равна 100.
32.
Площадь треугольника ABC равна 4.
ТочкиD, E – середины сторон
соответственноBC иAC. Найдите площадь
треугольника
Найдите площадь
треугольника
33. Площадь треугольника равна 12. Найдите площадь треугольника, вершинами которого являются середины сторон данного треугольника.
34. В треугольнике ABC точкиD, E – середины сторон соответственноBC иAC. Найдите площадь этого треугольника, если площадь треугольникаCDE равна 5.
35. Периметр треугольника равен 14, а радиус вписанной окружности равен 1. Найдите площадь треугольника.
36. Площадь треугольника равна 10, а его периметр равен 20. Найдите радиус вписанной окружности.
37. Площадь треугольника равна 20, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.
38. Площадь трапеции равна 12, высота равна 3, одно из оснований равно 5. Найдите другое основание.
39. Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
40.
Высота трапеции равна 10, площадь равна
150. Найдите среднюю линию трапеции.
Найдите среднюю линию трапеции.
41. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
42. Основания трапеции равны 6 и 2, боковая сторона, равная 4, образует с одним из оснований трапеции угол 30°. Найдите площадь трапеции.
43.
Найдите площадь прямоугольной трапеции,
основания которой равны 6 и 2, большая
боковая сторона составляет с основанием
угол 45
44. Найдите площадь трапеции, если ее средняя линия равна 5, а радиус вписанной окружности равен 2.
45. Найдите радиус окружности, вписанной в трапецию, если средняя линия трапеции равна 5, а площадь трапеции равна 40.
46. Площадь треугольника ABC равна 12, точки D и E – середины сторон соответственно BC и AC. Найдите площадь трапеции ABDE.
47.
Площадь параллелограмма ABCD равна 16.
48. Найдите площадь круга, диаметр которого равен 12.
49. Найдите радиус круга, площадь которого равна .
50. Найдите площадь круга, длина окружности которого равна 1.
51. Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны 3 и 4.
52. Площадь круга равна . Найдите длину его окружности.
53.
Найдите площадь сектора круга радиуса
6, центральный угол которого равен 60
54. Найдите площадь сектора круга радиуса 2, центральный угол которого равен 90о.
55. Найдите площадь сектора круга радиуса 3, центральный угол которого равен 120о.
56. Найдите площадь
круга, описанного около квадрата со
стороной, равной 1.
57. Найдите площадь круга, вписанного в квадрат со стороной 2.
58. Площадь круга, вписанного в квадрат, равна 1. Найдите площадь круга, описанного около этого квадрата.
59. Найдите площадь фигуры, изображенной на рисунке, ограниченной четырьмя дугами окружностей с центрами в вершинах единичного квадрата.
60. Найдите площадь фигуры, изображенной на рисунке, ограниченной двумя полуокружностями с центрами в серединах противоположных сторон единичного квадрата.
61. Найдите площадь фигуры, покрываемой четырьмя единичными кругами, изображенными на рисунке.
62. Найдите площадь фигуры, изображенной на рисунке, ограниченной тремя дугами окружностей с центрами в вершинах правильного треугольника со стороной, равной 2.
63. Найдите
площадь четырехугольника на координатной
плоскости, вершины которого имеют
координаты (-1, -2), (4, -2), (4, 2), (-1, 2).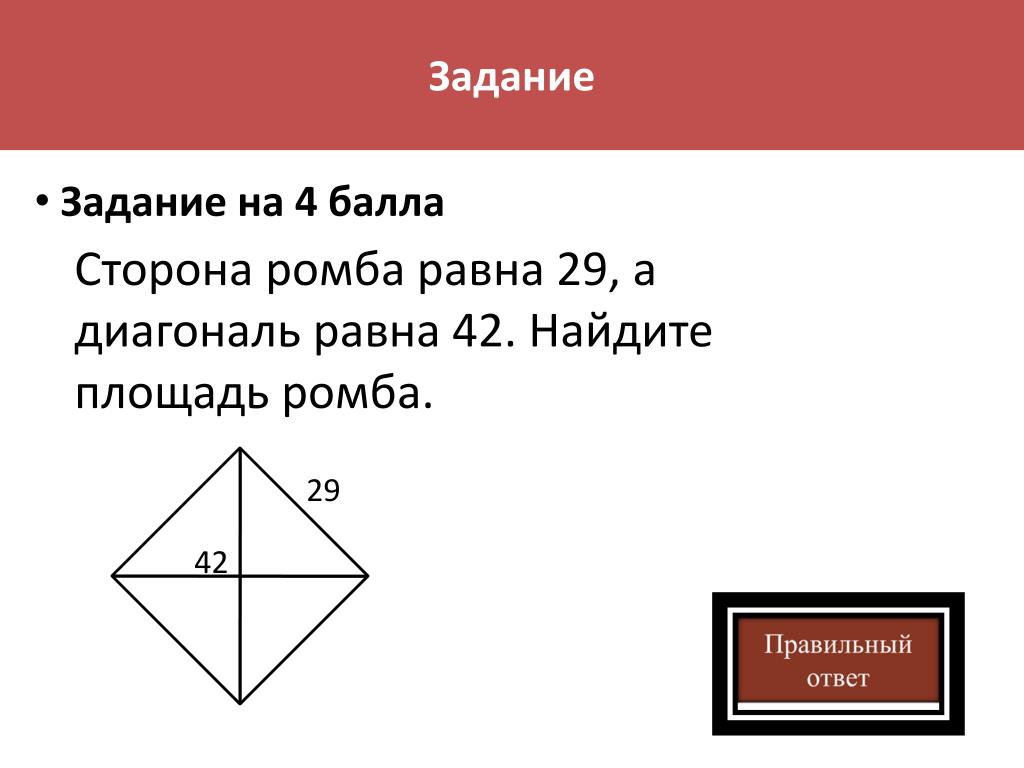
64. Найдите площадь четырехугольника на координатной плоскости, вершины которого имеют координаты (-2, 1), (3, 1), (3, 3), (-2, 3).
65. Найдите площадь четырехугольника на координатной плоскости, вершины которого имеют координаты (3, 0), (0, 2), (-3, 0), (0, -2).
66. Найдите площадь четырехугольника на координатной плоскости, вершины которого имеют координаты (0, 0), (3, 1), (4, 4), (1, 3).
67. Найдите площадь треугольника на координатной плоскости, вершины которого имеют координаты (-1, 0), (3, 0), (3, 4).
68. Найдите площадь треугольника на координатной плоскости, вершины которого имеют координаты (0, -2), (3, 3), (0, 3).
69. Найдите площадь трапеции на координатной плоскости, вершины которой имеют координаты (3, 0), (3, 1), (0, 3), (0, -1).
70. Найдите площадь
трапеции на координатной плоскости,
вершины которой имеют координаты (3,
-1), (3, 1), (0, 2), (0, -1).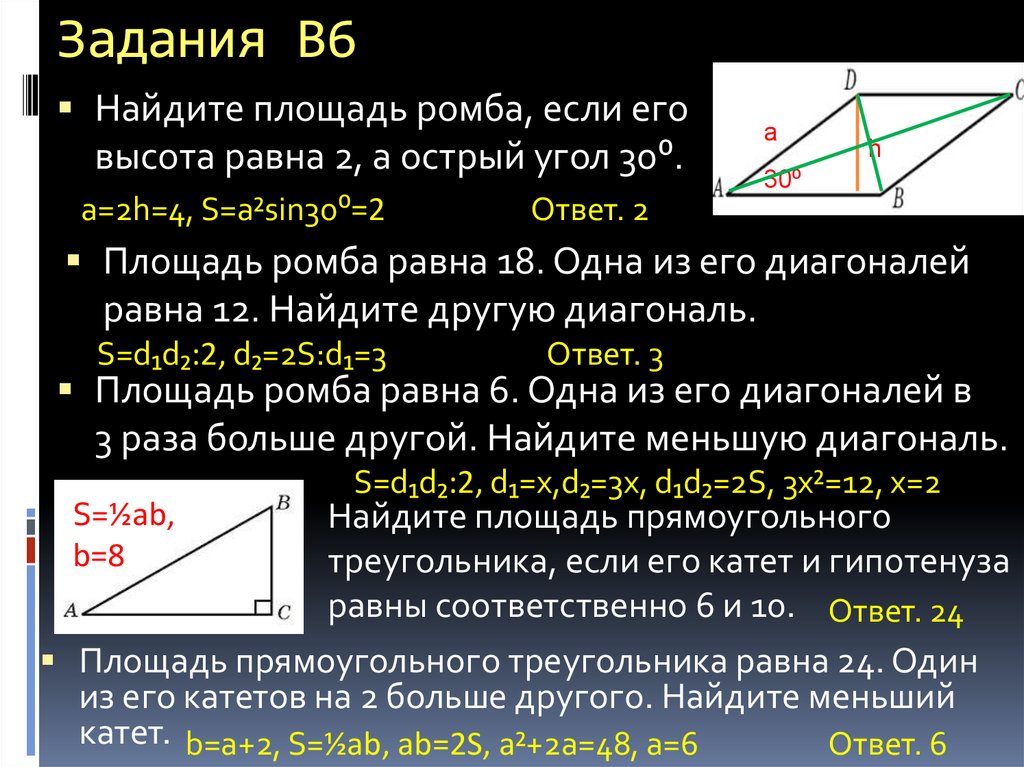
71. Найдите площадь круга на координатной плоскости с центром в точке A(2, 3), окружность которого проходит через начало координат.
72. Найдите площадь круга на координатной плоскости с центром в точке A(-2, -2), окружность которого касается оси ординат.
ЕГЭ Профиль №1. Квадрат, прямоугольник, параллелограмм, ромб — math200.ru
Skip to contentЕГЭ Профиль №1. Квадрат, прямоугольник, параллелограмм, ромбadmin2022-08-28T09:28:26+03:00
Скачать файл в формате pdf.
ЕГЭ Профиль №1. Квадрат, прямоугольник, параллелограмм, ромб
| Задача 1. В параллелограмме ABCD \(AB = 3,\;\;AD = 21,\;\;\sin A = \frac{6}{7}.\) Найдите большую высоту параллелограмма. Ответ ОТВЕТ: 18. |
Задача 2. Найдите площадь квадрата, если его диагональ равна 1. Ответ ОТВЕТ: 0,5. |
| Задача 3. Найдите диагональ квадрата, если его площадь равна 2. Ответ ОТВЕТ: 2. |
| Задача 4. Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой. Ответ ОТВЕТ: 18. |
| Задача 5. Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны. Ответ ОТВЕТ: 6. |
| Задача 6. Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2. Ответ ОТВЕТ: 18. |
| Задача 7. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2. Ответ ОТВЕТ: 18. |
| Задача 8. Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника. Ответ ОТВЕТ: 14. |
| Задача 9. Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника. Ответ ОТВЕТ: 48. |
| Задача 10. Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника. Ответ ОТВЕТ: 13. |
| Задача 11. Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника. Ответ ОТВЕТ: 48. |
| Задача 12. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность? Ответ ОТВЕТ: 2. |
| Задача 13. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах. Ответ ОТВЕТ: 30. |
Задача 14. \circ }\). \circ }\).Ответ ОТВЕТ: 1,5. |
| Задача 26. Найдите больший угол параллелограмма, если два его угла относятся как 3:7. Ответ дайте в градусах. Ответ ОТВЕТ: 126. |
| Задача 27. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах. Ответ ОТВЕТ: 90. |
| Задача 28. Две стороны параллелограмма относятся как 3:4, а периметр его равен 70. Найдите большую сторону параллелограмма. Ответ ОТВЕТ:20 . |
| Задача 29. Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма. Ответ ОТВЕТ: 20. |
Задача 30. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4:3, считая от вершины острого угла. \circ }\). Найдите угол ABC. Ответ дайте в градусах. \circ }\). Найдите угол ABC. Ответ дайте в градусах.Ответ ОТВЕТ: 94. |
| Задача 36. Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB. Ответ ОТВЕТ: 141,75. |
| Задача 37. Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A’B’C’D’, вершинами которого являются середины сторон данного параллелограмма. Ответ ОТВЕТ: 76,5. |
| Задача 38. Площадь параллелограмма ABCD равна 176. Точка E — середина стороны CD. Найдите площадь треугольника ADE. Ответ ОТВЕТ: 44. |
| Задача 39. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника. Ответ ОТВЕТ: 9. |
Реклама
Поддержать нас
Площадь ромба — Формула, Как найти площадь ромба
Площадь ромба — это количество пространства, заключенного или охваченного ромбом в двумерной плоскости. Ромб — это особый вид параллелограмма, у которого все стороны равны. Форму можно отличить от квадрата по величине внутреннего угла. Внутренний угол ромба не обязательно должен быть прямоугольным. Площадь ромба можно вычислить по-разному, в зависимости от известных нам параметров.
Ромб — это особый вид параллелограмма, у которого все стороны равны. Форму можно отличить от квадрата по величине внутреннего угла. Внутренний угол ромба не обязательно должен быть прямоугольным. Площадь ромба можно вычислить по-разному, в зависимости от известных нам параметров.
| 1. | Что такое площадь ромба? |
| 2. | Площадь ромба Формула |
| 3. | Как вычислить площадь ромба? |
| 4. | Часто задаваемые вопросы по области ромба |
Что такое площадь ромба?
Площадь ромба можно определить как количество пространства, ограниченного ромбом в двумерном пространстве. Он изображает общее количество единичных квадратов, которые могут в него поместиться, и измеряется в квадратных единицах (например, см 2 , м 2 , в 2 и т.д.). Ромб — параллелограмм, у которого противоположные стороны параллельны, противолежащие углы равны, а прилежащие углы смежны. Ниже приведены свойства формы.
Ниже приведены свойства формы.
- Ромб является равносторонним четырехугольником, потому что все стороны имеют одинаковую длину.
- Диагонали ромба пересекаются под прямым углом пополам.
- Диагонали являются биссектрисами угла.
- Площадь ромба можно найти разными способами: по основанию и высоте, по диагоналям и по тригонометрии.
Площадь ромба Формула
Для вычисления площади ромба можно использовать разные формулы в зависимости от известных нам параметров. Для вычисления площади ромба используются следующие формулы:
- Используя основание и высоту
- Использование диагоналей
- Использование тригонометрии
Формула площади ромба, если известны основание и высота
Ромб является параллелограммом. Мы знаем, что площадь параллелограмма получается путем умножения основания и высоты на квадратные единицы. То же самое относится и к ромбу.
Площадь ромба = основание × высота кв. единицы
единицы
Пример: Найдите площадь ромба, длина стороны которого 7 дюймов, а высота ромба 10 дюймов.
Решение: Как мы знаем, площадь = основание × единицы высоты 2
⇒ Площадь = 7 × 10 дюймов 2
⇒ Площадь = 70 дюймов 2
Формула площади ромба при известных диагоналях
Площадь ромба равна половине произведения длин диагоналей. Формула для вычисления площади ромба с использованием диагоналей дается как,
Площадь = (d 1 × d 2 )/2 кв. ед., где d 1 и d 2 — диагонали ромба.
Рассмотрим ромб ABCD. Пусть Е — точка пересечения двух диагоналей. Мы делаем следующие наблюдения:
- Четыре стороны конгруэнтны.
- Диагонали делятся пополам.
- Четыре внутренних угла с равными противоположными углами. ⇒ ∠ А = ∠ С и ∠ В = ∠ D
- Две диагонали AC и BD.
Площадь ромба ABCD = площадь ∆ ADC + площадь ∆ ABC
Площадь ромба = 2 × площадь ∆ ABC —(1) (∵ ∆ ABC конгруэнтна ∆ ADC)
Площадь ∆ ABC
= 1/2 × основание × высота
= 1/2 × АС × ВЕ
= 1/2 × AC × 1/2 × BD (∵BE = BD/2)
= 1/4 (AC × BD) — (2)
Площадь ромба ABCD
Площадь = 2 × 1/4 × AC × BD = 1/2 × AC × BD (Из (1) и ( 2))
⇒ Площадь = 1/2 × диагональ 1 × диагональ 2
∴ Площадь ромба = 1/2 × диагонали 1 × диагонали 2 единицы 2
Формула площади ромба, когда известны стороны и углы
Мы применяем концепцию тригонометрии при вычислении площади, когда стороны и углы известны. Мы можем использовать любой угол, потому что либо углы равны, либо они являются дополнительными, а дополнительные углы имеют один и тот же синус. Площадь ромба с учетом стороны и угла определяется как
Мы можем использовать любой угол, потому что либо углы равны, либо они являются дополнительными, а дополнительные углы имеют один и тот же синус. Площадь ромба с учетом стороны и угла определяется как
Площадь ромба = сторона 2 × sin(A) кв. единиц, где A — внутренний угол.
Пример: Какова площадь ромба, если длина его стороны 4 м, а один из углов А равен 30º.
Решение: Как известно, площадь ромба = s 2 × sin(30º)
Площадь ромба = s 2 × sin(30º) = 4 2 × 1/2
⇒ Площадь ромба = 16 × 1/2 = 8 кв. ярдов
Как вычислить площадь ромба?
Ниже описаны различные методы вычисления площади ромба. Существует три метода вычисления площади ромба, представленные как:
- Метод 1: Использование базы и высоты
- Метод 2: использование диагоналей
- Метод 3: использование тригонометрии
Площадь ромба с учетом основания и высоты
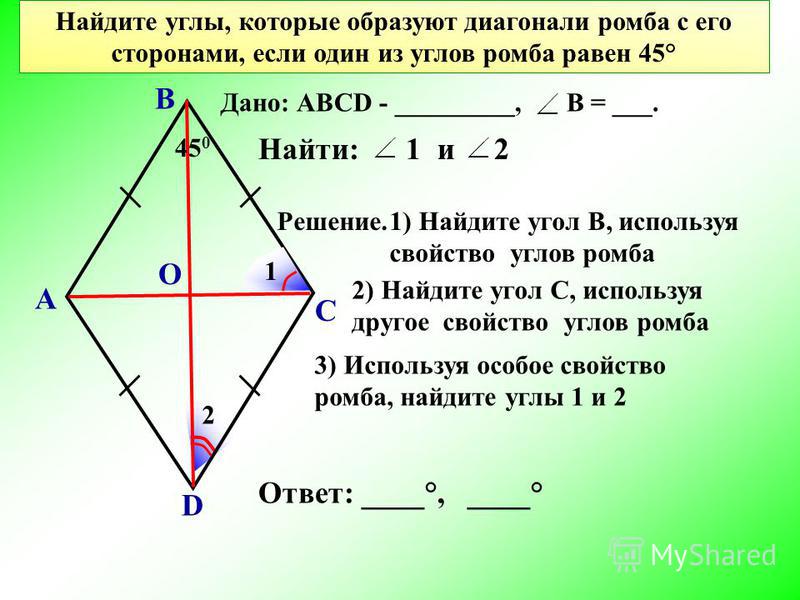
- Шаг 1: Найдите и запишите основание и высоту заданного ромба.
 Основание — одна из сторон ромба, а высота — расстояние по перпендикуляру от выбранного основания до противоположной стороны.
Основание — одна из сторон ромба, а высота — расстояние по перпендикуляру от выбранного основания до противоположной стороны. - Шаг 2: Умножьте основание и высоту.
Полученное значение даст площадь ромба.
Площадь ромба по диагоналям
Рассмотрим ромб ABCD, имеющий две диагонали, т. е. AC и BD.
- Шаг 1: Найдите длину обеих диагоналей, диагонали 1 и диагонали 2.
- Шаг 2: Умножьте обе длины, d1 и d2.
- Шаг 3: Разделите результат на 2.
Полученное значение даст площадь ромба ABCD.
Площадь ромба с помощью тригонометрии
- Шаг 1: Возведите в квадрат длину любой из сторон.
- Шаг 2: Умножьте его на синус любого из углов.
Полученное значение даст площадь ромба.
Пример: Рассмотрим ромб ABCD. AB, BC, CD, DA — конгруэнтные (равные) стороны. AC и BD — диагонали, и они пересекаются в E. Даны CD = 17 футов и AE = 8 футов. Найдите площадь ABCD.
AB, BC, CD, DA — конгруэнтные (равные) стороны. AC и BD — диагонали, и они пересекаются в E. Даны CD = 17 футов и AE = 8 футов. Найдите площадь ABCD.
Теперь мы знаем диагональ 1, AC = 16 футов.
Далее нам нужно рассчитать BD.
BD = BE + ED = 2 × BE
У нас все еще есть неизвестное, BE.
Теорема Пифагора утверждает, что
до н.э. 2 = BE 2 + EC 2
BC = 17 футов (∵ CD = BC, так как все стороны равны)
EC = 8 футов (∵ AE = EC, поскольку диагонали делятся пополам)
17 2 = ВЕ 2 + 8 2
⇒ БЭ 2 = 289 — 64
= 225
∴ BE = 15 футов и BD = 30 футов
Подставим все значения в области формулы ромба.
Площадь ромба = 1/2 × d 1 × d 2 квадратных единиц
= 1/2 × BD × AC кв. фут
= 1/2 × 30 × 16 кв. футов
⇒ Площадь ромба = 240 квадратных футов
Полезные советы:
- Помните, что высота не равна длине стороны ромба.

- Площадь ромба можно найти тремя способами: по диагоналям, по углу и стороне, по углу и высоте.
- Используйте теорему Пифагора, чтобы найти вторую диагональ, если известны меры одной диагонали и стороны.
Примеры на площади ромба
Пример 1: Используя формулу площади ромба, найдите площадь ромба, изображенного на рисунке ниже.
Решение:
Площадь ромба = 1/2 × BD × AC
BD = 2 × BE
= 2 × 8
= 16 ярдовAC = 2 × AE = 2 × 10 = 2 ярда
⇒ Площадь = 1/2 × 16 × 20
= 8 × 20
= 160 ярдов 2Ответ: Площадь ромба = 160 ярдов 2
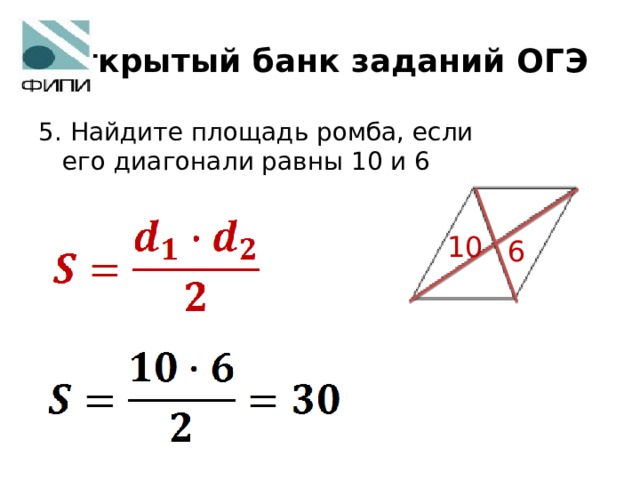
Пример 2: Стороны ромба ABCD равны 5 дюймов, а длина его одной диагонали АС равна 8 дюймам. Вычислите его площадь.
Решение:
Зная сторону и диагональ, найдем другую диагональ.
 Пусть О — точка пересечения диагоналей.
Пусть О — точка пересечения диагоналей.Площадь = (AC × BD)/2 кв. дюйма
⇒ АС = 8 в
. ⇒ AO = 4 дюйма (∵ AO = 1/2 AC)Чтобы найти другую диагональ BD, рассмотрим AOD.
По теореме Пифагора, AD 2 = AO 2 + OD 2
⇒ 25 2 = 4 2 + ОД 2
⇒ ОД 2 = 25 −16
⇒ ОД 2 = 9
⇒ ОД = 3 в
⇒ BD = 6 дюймов (∵BD = 2 × внешний диаметр)
Площадь = (8 × 6) ÷ 2 квадратных дюйма
Площадь = 24 квадратных дюймаОтвет: Площадь ромба = 24 квадратных дюйма
Пример 3: Площадь ромба равна 256 квадратных единиц. Если длина одной из диагоналей равна 8 единицам, найдите длину другой ее диагонали.
Решение:
Мы знаем, что площадь ромба можно вычислить с помощью диагоналей следующим образом: × диагональ 2 )
диагональ 2 = (256 × 2)/8
диагональ 2 = 64Ответ: Длина другой диагонали данного ромба = 64 единицы
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика — это жизненный навык. Помогите своему ребенку усовершенствовать это с помощью реального приложения с Cuemath.
Помогите своему ребенку усовершенствовать это с помощью реального приложения с Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по площади ромба
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по площади ромба
Какова площадь ромба?
Площадь ромба – это общее количество пространства, заключенного или охваченного ромбом в двухмерной плоскости. Он выражается в квадратных единицах (например, см 2 , м 2 , в 2 и т.д.).
Какая формула нахождения площади ромба?
Для вычисления площади ромба можно использовать разные формулы в зависимости от известных нам параметров. Используя основание и высоту, формула задается следующим образом: площадь ромба = основание × высота в квадратных единицах. Площадь ромба по диагоналям равна: Площадь = (d 1 × d 2 )/2 кв. ед., где d 1 и d 2 — диагонали ромба. Применяя концепцию тригонометрии с использованием стороны и угла, мы можем следовать формуле: Площадь ромба = сторона 2 × sin(A) квадратных единиц, где а — внутренний угол.
Применяя концепцию тригонометрии с использованием стороны и угла, мы можем следовать формуле: Площадь ромба = сторона 2 × sin(A) квадратных единиц, где а — внутренний угол.
Как найти сторону ромба по диагоналям?
Площадь ромба можно вычислить, используя длины диагоналей. Формула для нахождения площади в этом случае имеет следующий вид: Площадь = (d 1 × d 2 )/2 квадратных единиц, где d 1 и d 2 — диагонали ромба.
Равны ли площади ромба и квадрата?
Нет, площади ромба и квадрата не равны. Однако их площадь можно было бы рассчитать таким же образом, учитывая их размеры. Площадь ромба или любого параллелограмма = основание × высота. У ромба сторона и высота неодинаковы. Однако площадь квадрата = сторона×сторона, причем стороной может быть и высота квадрата. Квадрат является ромбом, потому что у него четыре стороны, и каждая сторона имеет одинаковую длину. Однако далее квадрат определяется как фигура, имеющая четыре равных угла по 9 градусов. 0 градусов. Следовательно, квадрат — это ромб. Однако ромб не обязательно является квадратом. Поэтому их площади не могут быть одинаковыми.
0 градусов. Следовательно, квадрат — это ромб. Однако ромб не обязательно является квадратом. Поэтому их площади не могут быть одинаковыми.
Как найти площадь ромба, зная сторону и высоту?
Площадь ромба можно вычислить, зная длину основания или стороны и высоту. Здесь под высотой понимается перпендикулярное расстояние между параллельными сторонами, одну из которых мы взяли за основу. Формула для нахождения площади в этом случае дается как площадь ромба = основание × высота кв.
В чем разница между площадью ромба и квадрата?
Площадь квадрата равна квадрату его стороны, т. е. s × s, где s — длина стороны квадрата, тогда как площадь ромба равна ½ × d1 × d2, где d1 и d2 — длины диагоналей.
В чем разница между площадью ромба и прямоугольника?
Площадь прямоугольника равна l × b, где «l» — длина прямоугольника, а «b» — длина прямоугольника, а площадь ромба равна ½ × d1 × d2, где d1 и d2 — длины диагоналей.
В чем разница между площадью ромба и его периметром?
Периметр ромба представляет собой общую меру его границы и рассчитывается путем сложения длин всех его сторон, тогда как площадь ромба или любых параллелограммов является произведением его основания и высоты, т.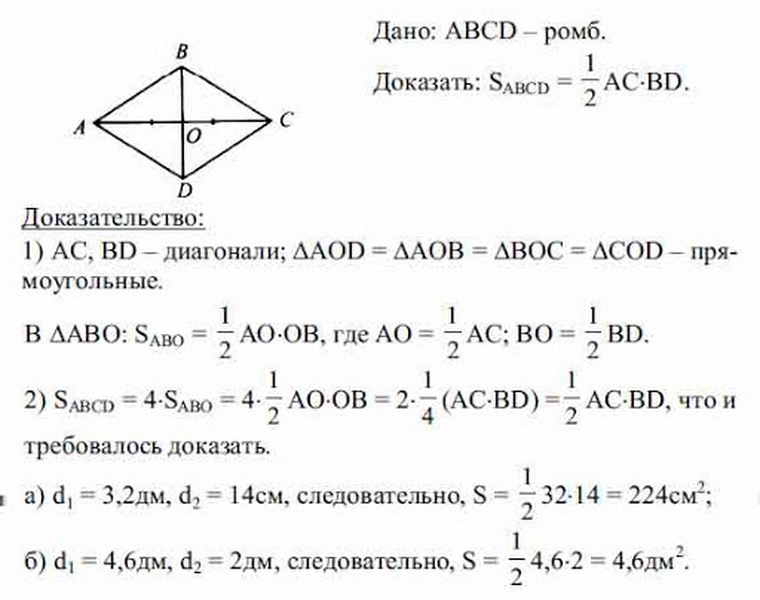 е. основание × высота. Следовательно, площадь ромба равна половине произведения ts диагоналей, заданных как ½ × d1 × d2, где d1 и d2 — длины диагоналей.
е. основание × высота. Следовательно, площадь ромба равна половине произведения ts диагоналей, заданных как ½ × d1 × d2, где d1 и d2 — длины диагоналей.
Для чего нужен калькулятор площади ромба?
Калькулятор площади ромба — это онлайн-инструмент, с помощью которого мы можем легко вычислить площадь ромба за считанные секунды. Чтобы определить значение, нам нужно ввести определенные параметры, такие как значение диагоналей. Попробуйте онлайн-калькулятор площади ромба Cuemath для быстрых вычислений и решите свои проблемы, связанные с площадью ромба, за считанные секунды.
Какова высота, если известна площадь ромба?
Чтобы вычислить высоту или высоту, когда дана площадь, нам нужна длина основания. Формула, которая может быть применена для расчета высоты, представлена в виде площади/базовых единиц.
Если площадь ромба 48 кв.см и одна из его диагоналей 6см, то найдите его высоту
Арья Р.
спросил 11.02. 18
18ОПРЕДЕЛЕНИЕ ВЫСОТЫ РОМБА ПО ЕГО ПЛОЩАДИ И ОДНОЙ ИЗ ЕГО ДИАГОНАЛЕЙ
Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Артур Д. ответил 11.02.18
Репетитор
4.9 (158)
Сорокалетний педагог: классная комната, летняя школа, заместитель, репетитор
Об этом репетиторе ›
Об этом репетиторе ›
A=48 кв. см
одна диагональ 6 см
пусть x и y будут двумя диагоналями
xy=2A
6y=2*48
6y=96
y=96/6
y=16 см для другой диагонали
900 ромбы пересекаются, образуя прямые углы, а также делят друг друга пополам при пересечении
нарисуйте ромб с двумя диагоналями
у вас есть четыре прямоугольных треугольника, которые все конгруэнтны
выберите один, скажем, тот, что справа
потому что диагонали делят друг друга пополам, одна сторона прямоугольного треугольника равна (1/2)(6)=3, а другая сторона равна 92=73
s=√73
s=8,544 см — это длина любой из четырех сторон и, следовательно, основание в формуле A=bh
Нарисуйте высоту правой стороны
A=bh
48=8,544*h
h=48/8,544
h=5,6179 см — высота ромба
Голосовать за 1 Понизить голос
Подробнее
Отчет
Кеннет С. ответил 11.02.18
ответил 11.02.18
Репетитор
4,8 (62)
Экспертная помощь по алгебре/тригонометрии/(пред)исчислению для гарантии успеха в 2018 году
См. таких репетиторов
Смотрите таких репетиторов
площадь = ½(dD), т. е. половина произведения длин его диагоналей.
также площадь = основание (высота) = сторона (высота)
I
Различные комбинации длины стороны и высоты могут привести к постоянной (известной) площади. Поэтому я не думаю, что можно получить один единственный ответ
Голосовать за 0 Понизить голос
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.

 Основание — одна из сторон ромба, а высота — расстояние по перпендикуляру от выбранного основания до противоположной стороны.
Основание — одна из сторон ромба, а высота — расстояние по перпендикуляру от выбранного основания до противоположной стороны.
 Пусть О — точка пересечения диагоналей.
Пусть О — точка пересечения диагоналей.
Leave A Comment