Через среднюю линию основания треугольной призмы
27068. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Сказано, что плоскость проходит через среднюю линию основания, то есть через точки, которые являются серединами соседних сторон треугольника. При чём она проходит параллельно боковому ребру – это означает, что указанная плоскость также проходит через середины соответствующих соседних сторон другого основания.
Без каких-либо вычислений понятно, что площадь боковой поверхности отсечённой призмы будет в два раза меньше, чем у исходной.
Посмотрите! Высота у призм общая. Указанная плоскость разрезает две соседние боковые грани пополам.
Рассмотрим третью грань (параллельную плоскости сечения) – её площадь поверхности также в два раза меньше, так как средняя линия треугольника в два раза меньше параллельной ей стороны треугольника.
Учитывая, что высота остаётся неизменной (общая для обеих призм), можем сделать вывод, что площадь боковой поверхности (сумма площадей всех трёх граней) отсечённой призмы будет в два раза меньше.
Ответ: 12
27153. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Площадь боковой поверхности призмы:Значит для отсечённой призмы:Высота у пирамид общая, поэтому площадь боковой поверхности исходной призмы зависит от величины периметра. Он увеличился в два раза, так как средняя линия проходит через середины соседних сторон и равна половине третьей стороны треугольника. А это означает, что и площадь боковой поверхности так же будет больше в 2 раза. Следовательно она равна 16.
Ответ: 16
27106. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру.
Найдите объем отсеченной треугольной призмы.
Объём призмы равен произведению площади основания на высоту:То есть на величину обьема влияет площадь основания (высота неизменна). И объем меняется пропорционально изменению площади основания.
Треугольник лежащий в основании исходной призмы подобен треугольнику лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего).
Известно что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть если принять что:Площадь основания данной призмы больше площади основания отсечённой призмы в 4 раза. Таким образом, и объем исходной призмы в 4 раза больше объема отсеченной.
Ответ: 8
27107. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
*Все рассуждения представлены в предыдущей задаче.
**Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем исходной призмы будет в 4 раза больше объема отсечённой призмы.
Таким образом, искомый объём равен 20.
Ответ: 20
Через среднюю линию основания треугольной призмы
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2015-05-28
Здравствуйте! Очередная порция задачек с призмами, рассматриваются треугольные призмы. Объединил несколько заданий схожих по одному «признаку» – у них через среднюю линию основания проходит сечение. Вопросы стоят о вычислении площади поверхности или объёма либо исходной призмы, либо отсечённой. Что важно здесь помнить?
Это свойство подобия фигур касающееся площади, в частности про треугольник уже речь была в одной из статей, посмотрите (п.2). Но даже, если вы вдруг забудете это, представленные задачи будут интуитивно понятны и решите вы их в одно действие.
77111. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 6, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Сказано, что плоскость проходит через среднюю линию основания, то есть через точки, которые являются серединами соседних сторон треугольника. При чём она проходит параллельно боковому ребру – это означает, что указанная плоскость также проходит через середины соответствующих соседних сторон другого основания.
Без каких-либо вычислений понятно, что площадь боковой поверхности отсечённой призмы будет в два раза меньше, чем у исходной.
Посмотрите!
Высота у призм общая. Указанная плоскость разрезает две соседние боковые грани пополам.
Рассмотрим третью грань (параллельную плоскости сечения) – её площадь поверхности также в два раза меньше, так как средняя линия треугольника в два раза меньше параллельной ей стороны треугольника.
Учитывая, что высота остаётся неизменной (общая для обеих призм), можем сделать вывод, что площадь боковой поверхности (сумма площадей всех трёх граней) отсечённой призмы будет в два раза меньше.
Ответ: 3
76147. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 20. Найдите площадь боковой поверхности исходной призмы.
Задача обратная предыдущей. Формула для площади боковой поверхности призмы:
Значит для отсечённой призмы:
Высота у пирамид общая, поэтому площадь боковой поверхности исходной призмы зависит от периметра. Поскольку получившиеся треугольники в основании призмы подобны, и их соответствующие стороны относятся как 1:2, значит периметр основания исходной призмы вдвое больше периметра основания отсечённой.
А это означает, что и площадь боковой поверхности так же больше в 2 раза и равна 40.
Ответ: 40
27106.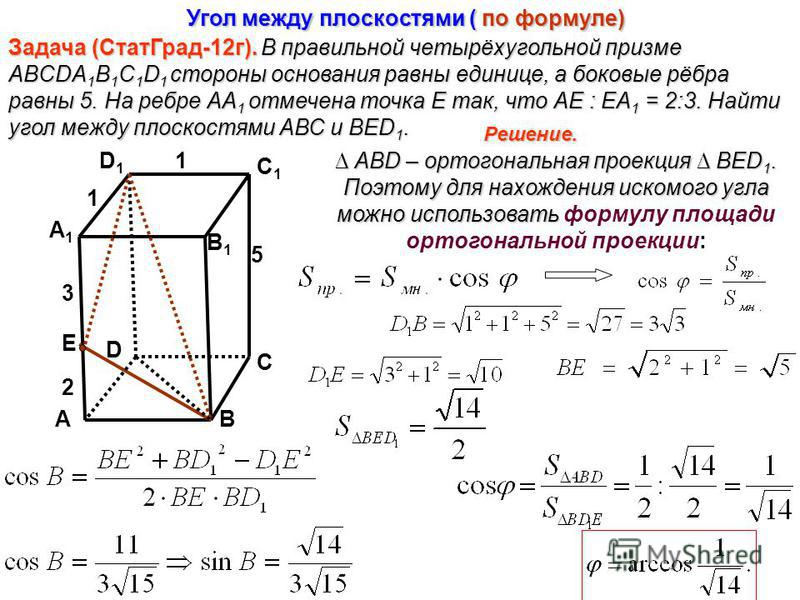
Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Известно, что объём призмы равен произведению площади основания и высоты. Высота для указанных призм общая, значит изменение объёма зависит только от изменения площади поверхности.
Рассмотрим треугольники лежащие в основаниях призм – они подобны. Если рассматривать основание исходной призмы относительно основания отсечённой, то коэффициент подобия будет равен 2. Что это нам даёт?
Мы знаем, что пощади подобных фигур соотносятся как квадрат коэффициента подобия, значит:
Основание отсечённой призмы в 4 раза меньше.
Таким образом, и её объём будет в 4 раза меньше, то есть 8.
Формально можно расписать так:
Ответ: 8
74745. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 7.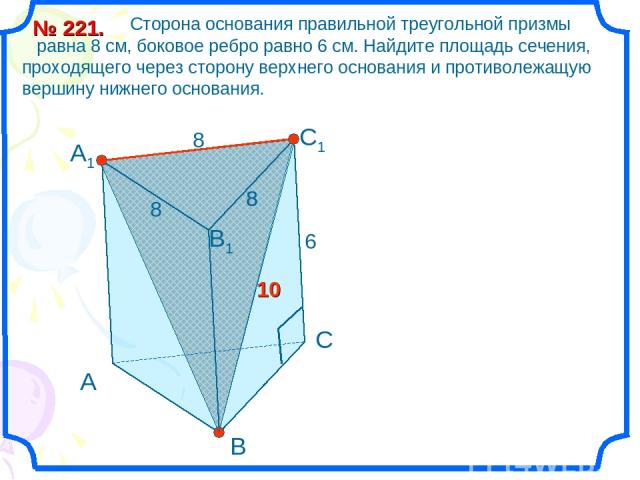
Найдите объем исходной призмы.
Задача обратная предыдущей. Объём призмы равен произведению площади основания на высоту:
Высота общая, значит объём меняется в зависимости от изменения площади основания.
Треугольник лежащий в основании исходной призмы, как уже сказано, подобен треугольнику лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию.
Площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть:
Таким образом, площадь основания исходной призмы больше площади основания отсечённой призмы в 4 раза.
Следовательно объем исходной призмы будет в 4 раза больше объема отсечённой призмы. Таким образом, искомый объём равен 28.
Ответ: 28
Ещё три задачи про площадь поверхности призмы
245356. Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза?
Увеличим все рёбра призмы в три раза.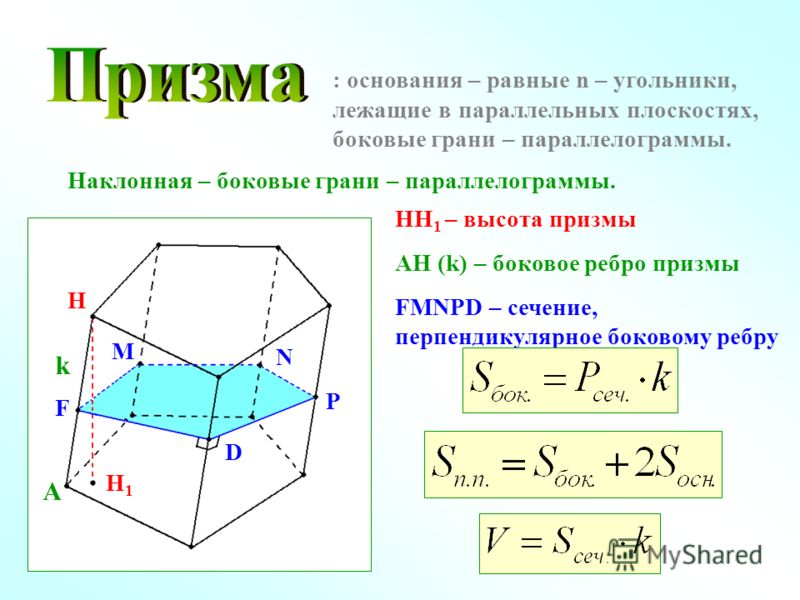
Что получается?
Получается, что каждая грань полученной призмы и соответствующая ей грань исходной призмы являются подобными фигурами. При чём коэффициент подобия равен 3. Мы, что площади подобных фигур пропорциональны квадрату коэффициента подобия, то есть:
Это означает, что площадь каждой отдельной грани нашей призмы увеличится в 9 раз. Так как площадь поверхности всей призмы это сумма площадей всех граней, то разумеется, что и вся площадь поверхности призмы также увеличится в 9 раз.
Ответ: 54
*На самом деле не важно о каком теле идёт речь (о призме, пирамиде, кубе, параллелепипеде), суть одна.
В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 30 и отстоит от других боковых ребер на 3 и 4. Найдите площадь боковой поверхности этой призмы.
На момент написания статьи эта задача из открытого банка заданий ЕГЭ удалена, но мы её рассмотрим, так вернуться может туда в любой момент, а значит и быть на экзамене в будущие годы.
Для вычисления боковой поверхности призмы воспользуемся формулой:
В данном случае боковое ребро это общее ребро перпендикулярных друг другу граней, оно равно 30. Перпендикулярным сечением призмы является прямоугольный треугольник с катетами 3 и 4. По теореме Пифагора найдём его гипотенузу и сможем вычислить периметр:
Таким образом:
Второй путь решения!
Указанная выше формула для кого-то может быть не понятна. В чём её смысл и что она выражает?
Посмотрите на каждую отдельную грань (положив призму на бок) – это параллелограммы. При чём основания этих параллелограммов равны и равны они боковому ребру, то есть 30. Высоты у них будут разные.
Две нам известны 3 и 4, третья не известна. Но её мы можем найти. Разрежем призму перпендикулярно боковым рёбрам, сечением разреза будет прямоугольный треугольник с катетами 3 и 4, найдём гипотенузу:
Получается, что площадь боковой поверхности равна сумме площадей трёх параллелограммов:
Ответ: 360
72605.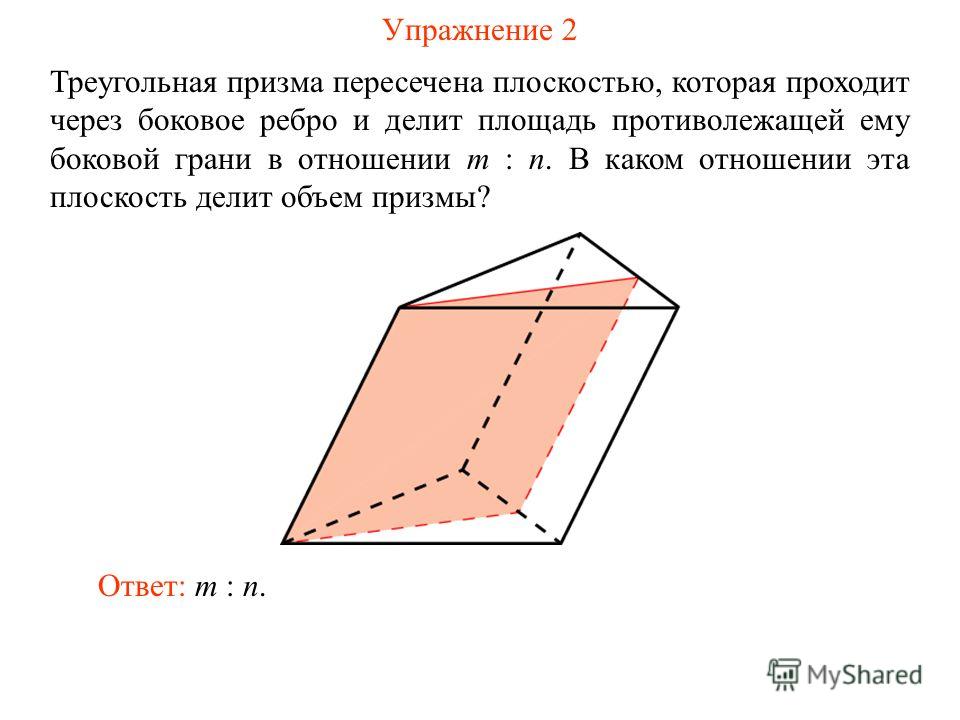
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 6, а высота 2.
Призма правильная, значит гранями являются равные по площади прямоугольники. Так как призма шестиугольная, то имеем 6 таких прямоугольников. Площадь боковой поверхности равна сумме площадей всех боковых граней:
Ответ: 72
РЕШИТЕ САМОСТОЯТЕЛЬНО
27068. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Посмотреть решение
27107. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Посмотреть решение
27153. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру.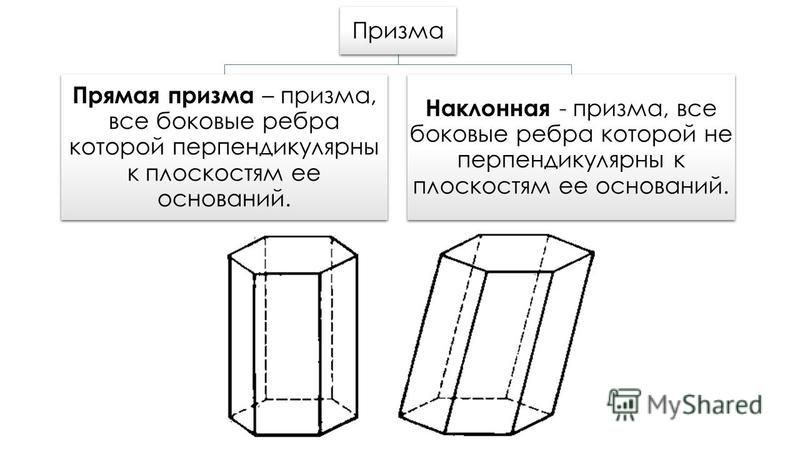
Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Посмотреть решение
27150. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
Посмотреть решение
27057. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота 10.
Посмотреть решение
На этом всё, всего доброго!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Стереометрия ПРИЗМЫ | ЕГЭ-№2ОбъёмПлощадь
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Через среднюю линию треугольной призмы проведена плоскость. Через среднюю линию основания треугольной призмы
Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проводят плоскость, параллельную боковому ребру. Найдите
площадь боковой поверхности отсеченной треугольной призмы.
Помогите решить 2 задачи по геометрии!!! 1. Радиус шара 6дм, через конец радиуса проведена плоскость, лежащая на сфере под углом 30
градуса по радиусу. Найдите S сечений плоскости и S сфер.
2. Через конец радиуса, лежащего на сфере под углом 60 градусов к радиусу, проведена плоскость. Расстояние от центра сферы до этой плоскости равно 8 см. Найдите S сечений шара плоскостью и S сферой
1) Стороны основания правильной четырехугольной пирамиды равны 22, боковых ребер 61. Найдите площадь поверхности этой пирамиды.
2) Стороны основания правильной четырехугольной пирамиды равны 40, боковых ребер 29.
Найдите площадь поверхности этой пирамиды.
3) Стороны основания правильной шестиугольной пирамиды равны 66, боковых ребер 183. Найдите площадь боковой поверхности этой пирамиды.
4) Стороны основания правильной шестиугольной пирамиды равны 48, боковых ребер 74. Найдите площадь боковой поверхности этой пирамиды.
5) Найдите площадь поверхности правильной четырехугольной пирамиды, у которой стороны основания равны 16, а высота 15.
6) Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой 70, а высота 12.
7) В правильной четырехугольной пирамиде SABCD точка О — центр основания, S — вершина, SC =68, АС=120. Найдите длину СО.
8) В правильной четырехугольной пирамиде SABCD точка O — центр основания, S — вершина, SB=100, AC=120. Найдите длину СО.
9) В правильной четырехугольной пирамиде SABCD точка O — центр основания, S — вершина, SO=80, AC=120. Найдите боковое ребро SB.
10) В правильной четырехугольной пирамиде SABCD точка O — центр основания, S — вершина, SO=72, BD=42.
Найдите боковое ребро SA.
11) В правильной четырехугольной пирамиде SABCD точка O — центр основания, S — вершина, SO=16, SC=34. Найдите длину отрезка BD.
12) В правильной четырехугольной пирамиде SABCD точка O — центр основания, S — вершина, SO=32,SC=68. Найдите длину отрезка АС.
13) Основанием пирамиды является прямоугольник со сторонами 5 и 6. Его объем равен 50. Найдите высоту этой пирамиды.
14) Основанием пирамиды является прямоугольник со сторонами 4 и 8. Его объем равен 96. Найдите высоту этой пирамиды.
Пожалуйста, без формулы Герона.
В правильной треугольной призме через среднюю линию основания под углом 60 к плоскости основания проведена плоскость, пересекающая боковое ребро
Здравствуйте! Еще одна порция задач с призмами, рассмотрены треугольные призмы. Он объединил несколько похожих задач в один «знак» — они имеют разрез по средней линии основания. Вопросы касаются расчета площади поверхности или объема либо исходной призмы, либо отсеченной.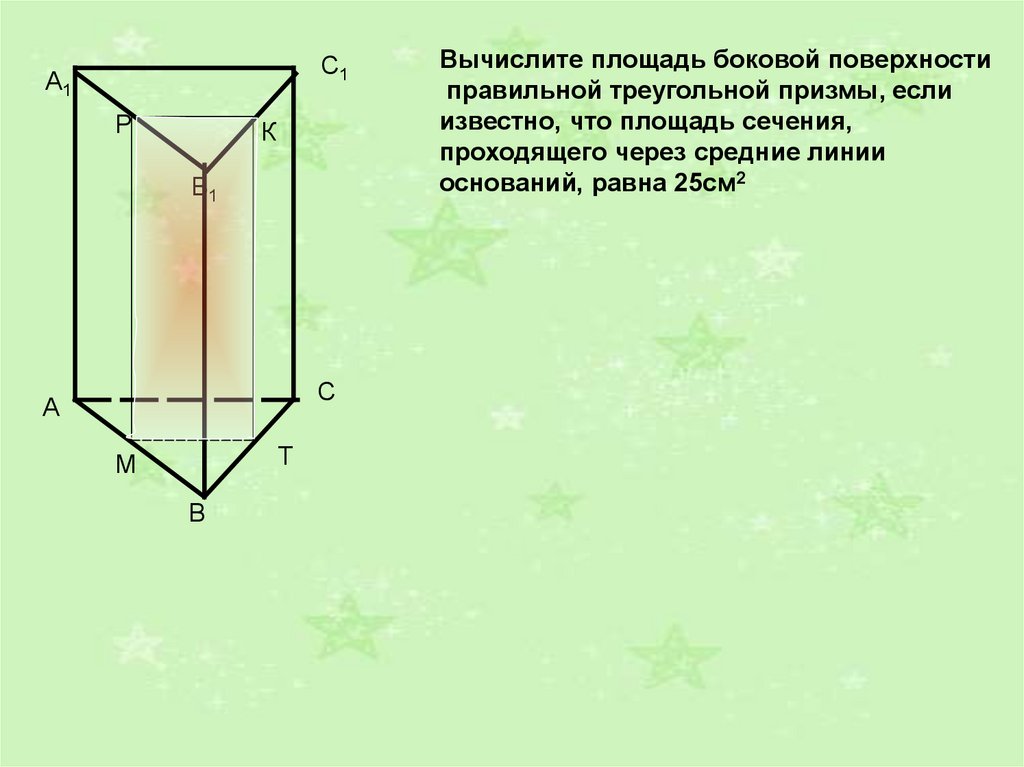
Что здесь важно помнить?
Это свойство подобия фигур относительно площади, в частности, треугольника уже обсуждалось в одной из статей, . Но даже если вы вдруг его забудете, представленные задачи будут интуитивно понятными и вы решите их за один шаг.
77111. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 6, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Говорят, что плоскость проходит через среднюю линию основания, то есть через точки, являющиеся серединами смежных сторон треугольника. При этом она проходит параллельно боковой кромке — это означает, что указанная плоскость также проходит через середины соответствующих смежных сторон другого основания.
Без всяких расчетов видно, что площадь боковой поверхности отсеченной призмы будет вдвое меньше исходной.
Смотри!
Высота призм обычная. Указанная плоскость делит две смежные боковые грани пополам.
Рассмотрим третью грань (параллельную плоскости сечения) — площадь ее поверхности также вдвое меньше, так как средняя линия треугольника вдвое меньше стороны треугольника, параллельной ей.
Учитывая, что высота остается неизменной (общей для обеих призм), можно сделать вывод, что площадь боковой поверхности (сумма площадей всех трех граней) отсеченной призмы будет вдвое меньше.
Ответ: 3
76147. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 20. Найдите площадь боковой поверхности исходной призмы.
Проблема обратная предыдущей. Fформула площади боковой поверхности призмы:
Итак, для отсеченной призмы:
Пирамиды имеют общую высоту, поэтому площадь боковой поверхности исходной призмы зависит от периметра. Так как получившиеся треугольники в основании призмы подобны, а их соответствующие стороны связаны как 1:2, то периметр основания исходной призмы вдвое больше периметра основания отсеченной.
А это значит, что площадь боковой поверхности тоже в 2 раза больше и равна 40.
Ответ: 40
27106. Через среднюю линию основания треугольной призмы, объем которой равен 32, проходит плоскость проводится параллельно боковой кромке. Найдите объем отсеченной треугольной призмы.
Мы знаем, что объем призмы равен произведению площади основания на высоту. Высота у этих призм общая, а значит, изменение объема зависит только от изменения площади поверхности.
Рассмотрите треугольники, лежащие в основаниях призм — они подобны. Если рассматривать основание исходной призмы относительно основания отсеченной, то коэффициент подобия будет равен 2. Что нам это дает?
Мы знаем, что пропорции подобных фигур связаны как квадрат коэффициента подобия, что означает:
Основание отрезной призмы в 4 раза меньше.
Таким образом, его объем будет в 4 раза меньше, то есть 8.
Формально это можно записать так:
Ответ: 8
74745.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 7. Найдите объем исходной призмы.
Проблема обратная предыдущей. Объем призмы равен произведению площади основания на высоту:
Высота общая, значит объем меняется в зависимости от изменения площади основания .
Треугольник, лежащий в основании исходной призмы, как уже было сказано, подобен треугольнику, лежащему в основании отсеченной призмы. Коэффициент сходства равен 2, так как сечение проведено по средней линии.
Площади подобных фигур связаны как квадрат коэффициента подобия, то есть:
Таким образом, площадь основания исходной призмы в 4 раза больше площади основания разреза -откл. призмы.
Следовательно, объем исходной призмы будет в 4 раза больше объема отсеченной призмы. Таким образом, искомый объем равен 28,
Ответ: 28
Еще три задачи на площадь поверхности призмы
245356.
Площадь поверхности правильной треугольной призмы равна 6. Чему будет равна площадь поверхности призмы, если все его ребра утраиваются?
Увеличим все ребра призмы в три раза. Что происходит?
Получается, что каждая грань получившейся призмы и соответствующая ей грань исходной призмы являются подобными фигурами. При этом коэффициент подобия равен 3. Мы, что площади подобных фигур пропорциональны квадрату коэффициента сходства, то есть:
Это означает, что площадь каждой отдельной грани нашей призмы увеличится в 9 раз. Поскольку площадь поверхности всей призмы равна сумме площадей всех граней, само собой разумеется, что вся площадь поверхности призмы также увеличится в 9 раз.
Ответ: 54
* На самом деле неважно, о каком теле идет речь (о призме, пирамиде, кубе, параллелепипеде), суть одна.
В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 30 и находится на расстоянии 3 и 4 от других боковых ребер. Найдите площадь боковой поверхности этой призмы.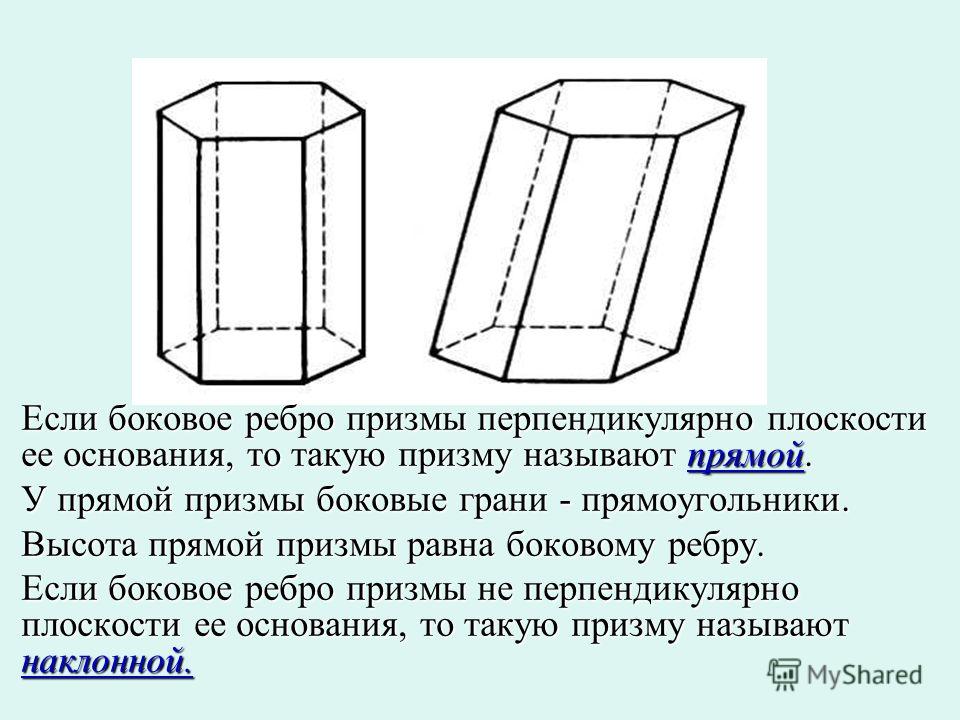
На момент написания статьи данное задание удалено из открытого банка заданий ЕГЭ, но мы его учтем, поэтому оно может вернуться туда в любой момент, а значит быть на ЕГЭ в последующие годы.
Для расчета боковой поверхности призмы воспользуемся формулой:
В данном случае боковое ребро – это общее ребро граней, перпендикулярных друг другу, оно равно 30. Перпендикулярное сечение призмы – это прямоугольный треугольник с катетами 3 и 4. По теореме Пифагора найдем его гипотенузу и сможем вычислить периметр:
Таким образом:
Второе решение!
Приведенная выше формула может быть кому-то непонятна. В чем его смысл и что он выражает?
Посмотрите на каждую грань в отдельности (положив призму на бок) — это параллелограммы. При этом основания этих параллелограммов равны и они равны боковому ребру, то есть 30. Их высоты будут различны.
Два нам известны 3 и 4, третий не известен. Но мы можем найти его. Разрежем призму перпендикулярно боковым граням, сечение разреза будет прямоугольным треугольником с катетами 3 и 4, найдем гипотенузу:
Получается, что площадь боковой поверхности равна сумме площадей трех параллелограммов:
Ответ: 360
72605.
Найти площадь боковой поверхности правильного шестиугольника призма со стороной основания 6 и высотой 2.
Решение.
Ответ: 12.
Ответ: 12
Площадь боковой поверхности треугольной призмы равна 6. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
прототип.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Ответ: 3
Площадь боковой поверхности треугольной призмы равна 26. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Ответ: 13
Площадь боковой поверхности треугольной призмы равна 28. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.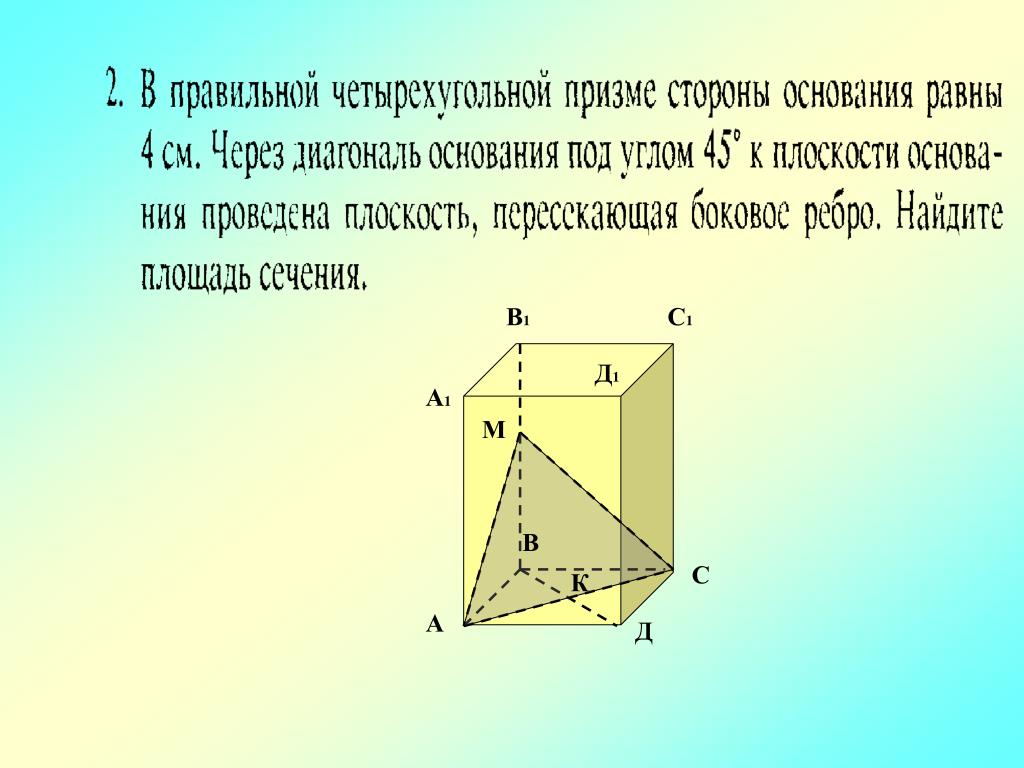
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Площадь боковой поверхности треугольной призмы равна 4. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Площадь боковой поверхности треугольной призмы равна 34. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Ответ: 17
Площадь боковой поверхности треугольной призмы равна 96. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Площадь боковой поверхности треугольной призмы равна 54. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани.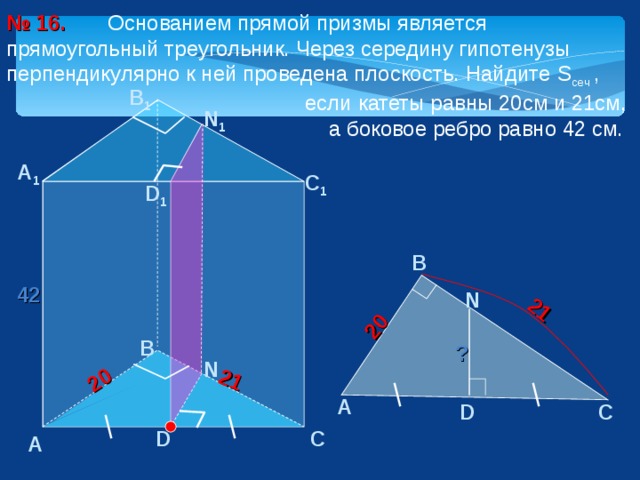
Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Ответ:
Площадь боковой поверхности треугольной призмы равна 82. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы.
Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Площадь боковой поверхности треугольной призмы равна 2. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Ответ: 1
Площадь боковой поверхности треугольной призмы равна 40.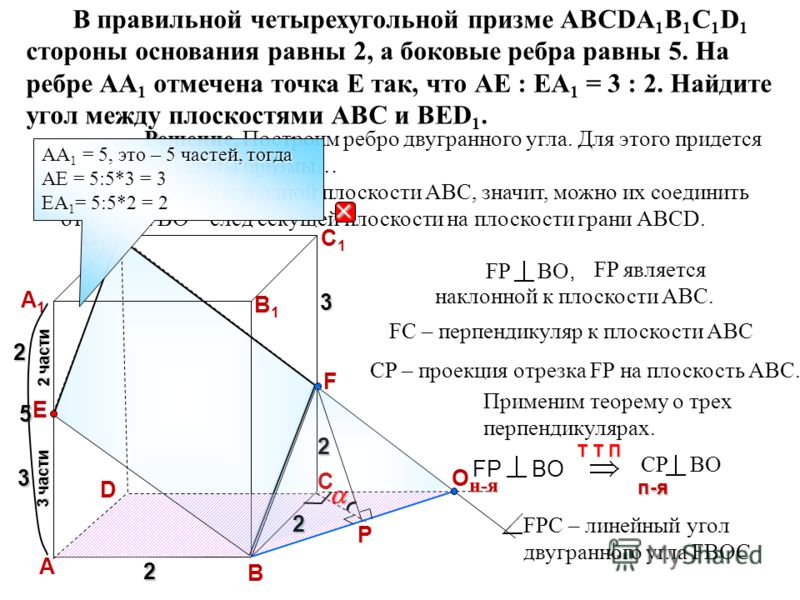
Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Ответ: 20
Площадь боковой поверхности треугольной призмы равна 76. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Ответ: 38
Площадь боковой поверхности треугольной призмы равна 14. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.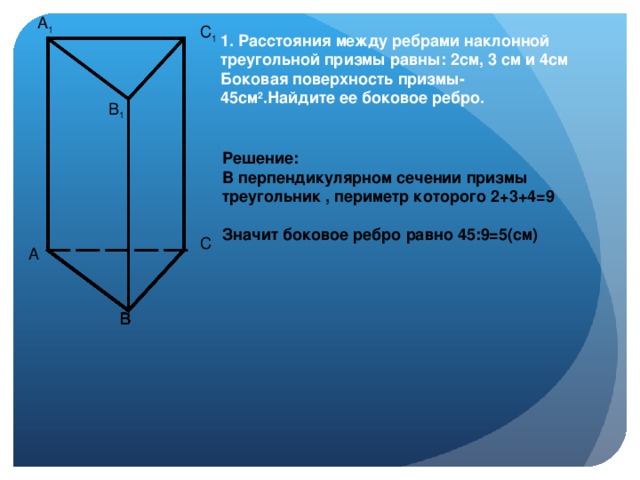
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Площадь боковой поверхности треугольной призмы равна 18. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Площадь боковой поверхности треугольной призмы равна 60. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Площадь боковой поверхности треугольной призмы равна 30. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.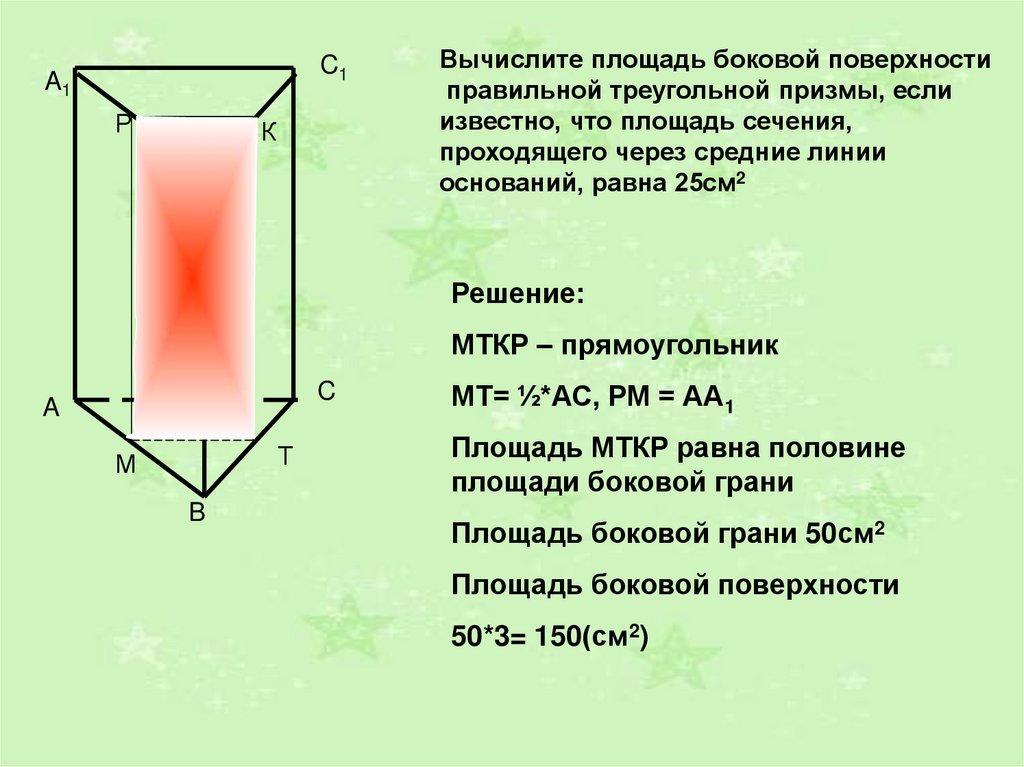
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Ответ: 15
Площадь боковой поверхности треугольной призмы равна 44. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани.
Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Ответ: 11
Площадь боковой поверхности треугольной призмы равна 62. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы.
Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Площадь боковой поверхности треугольной призмы равна 68. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Ответ: 12.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру.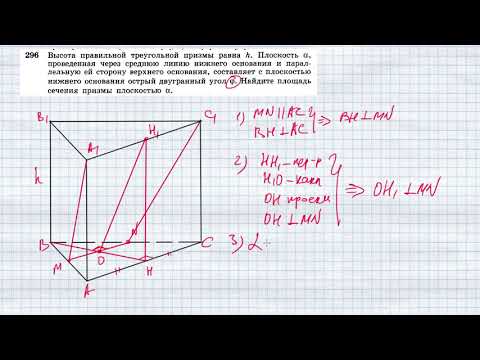
Найдите площадь боковой поверхности отсеченной треугольной призмы.
Решение.
Эта задача еще не решена, приводим решение прототипа.
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковой грани. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Площадь боковых граней отсеченной призмы составляет половину соответствующих площадей боковых граней исходной призмы. Следовательно, площадь боковой поверхности отсеченной призмы составляет половину площади боковой поверхности исходной.
Боковая площадь призмы Определения и примеры
Боковая площадь призмы Определения и примеры
Введение
Что приходит вам на ум, когда вы думаете о призме? Может быть, форма цветка? Может быть, цвета радуги? Если да, то поздравляю — вы не одиноки. В этом сообщении блога мы рассмотрим боковую область призмы, а также определения и примеры.
Таким образом, вы лучше поймете концепцию и сможете использовать ее в будущих математических задачах.
Что такое боковая площадь треугольной призмы?
Треугольные призмы представляют собой геометрическую фигуру, которая часто используется для обозначения боковой части фигуры. Треугольную призму можно использовать во многих реальных приложениях, таких как проектирование, архитектура и производство. Площадь боковой стороны треугольной призмы определяется как длина наибольшей стороны.
Ниже приведены примеры использования боковой поверхности треугольной призмы в различных областях:
Инженерное дело: боковая площадь может использоваться для расчета размера объекта или площади поверхности компонента.
Архитектура: боковую область можно использовать для расчета размера или планировки внутреннего пространства.
Производство: боковую область можно использовать для расчета размера или количества материалов.
Боковая площадь треугольной призмы Формула
Треугольная призма представляет собой трехмерную геометрическую фигуру, имеющую две боковые грани и одно основание.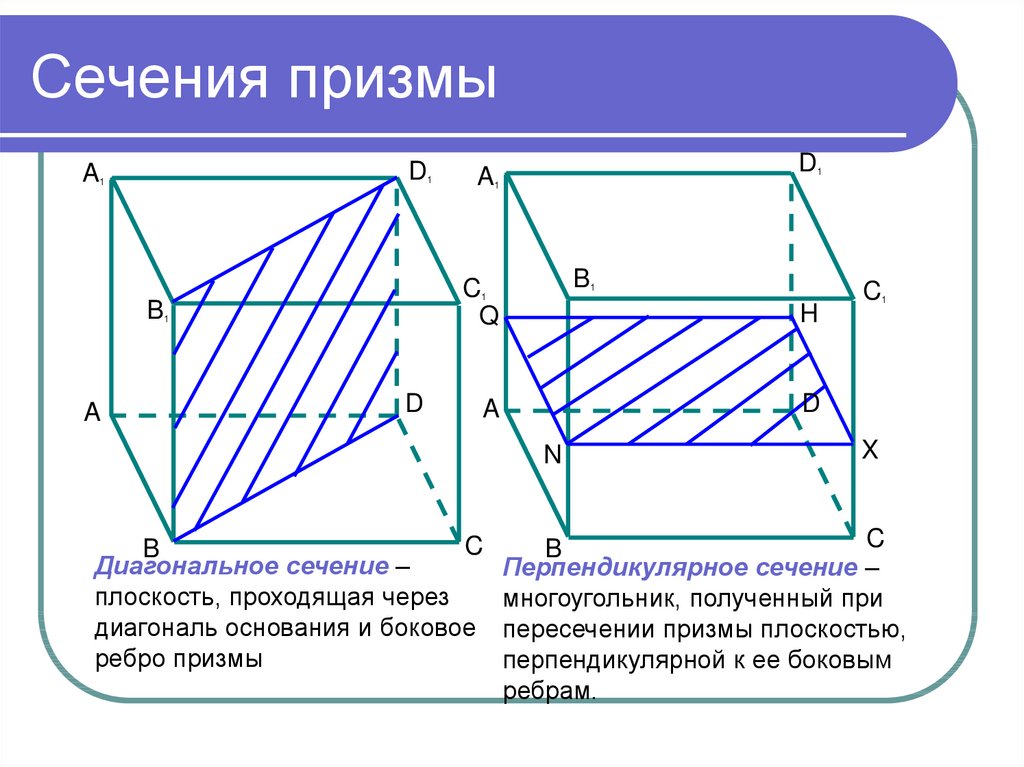
Площадь боковой поверхности треугольной призмы определяется путем умножения длины каждой стороны на ее ширину. Боковую площадь можно рассчитать по формуле Герона или по правилу Симпсона. В формуле Герона используется следующее уравнение:
, где «А» — длина одной стороны, «В» — длина другой стороны, а «W» — ширина треугольника. Правило Симпсона использует следующее уравнение:
, где «h» — высота треугольника, «b» — длина основания, а «t» — толщина данного материала.
Как найти формулу площади боковой поверхности треугольной призмы?
Площадь боковой поверхности треугольной призмы (LSA) = ah + bh + ch (или) (a + b + c) h.
Площадь боковой поверхности треугольной призмы равна сумме длин трех ее оснований.
Что такое боковые грани треугольной призмы?
Треугольные призмы представляют собой трехсторонние формы, которые обычно используются в геометрии и технике.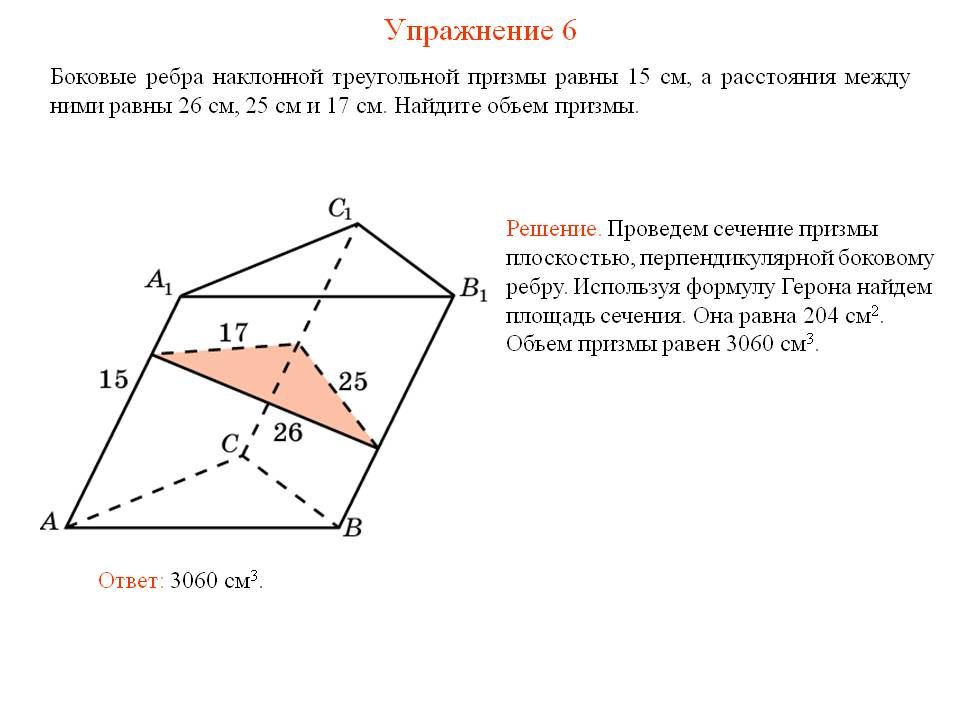
У них есть боковые грани, которые все похожи по форме и размеру. Площадь боковой поверхности треугольной призмы равна сумме площадей двух ее противоположных граней.
Площадь боковой поверхности прямоугольного треугольника равна длине его гипотенузы (стороны, противоположной прямому углу). Площадь боковой стороны левостороннего треугольника равна длине его наибольшей стороны. Площадь боковой поверхности треугольной призмы равна сумме площадей двух противоположных граней.
Площадь боковой поверхности прямоугольного треугольника равна длине его гипотенузы (стороны, противолежащей прямому углу). Площадь боковой стороны левостороннего треугольника равна длине его наибольшей стороны. Средняя площадь (или базальная грань) треугольной призмы имеет вдвое большую боковую площадь, чем каждая смежная грань.
Чем боковая грань треугольной призмы отличается от основания?
Боковая грань треугольной призмы отличается от основания, поскольку боковая грань имеет три угла при основании, а не два.
Боковую грань треугольной призмы также можно назвать внешним углом.
Треугольную призму можно разложить на два угла при основании, внутренний угол и боковую грань. Углы при основании измеряются от основания до самой длинной стороны призмы. Внутренний угол измеряется от центральной линии призмы до ближайшего к центру края треугольника. Боковая грань определяется как треугольник, соответствующий этим трем углам.
Боковая грань чаще всего используется в задачах геометрии, связанных с прямоугольными треугольниками. Предположим, у вас есть прямоугольный треугольник с одной вершиной в начале координат, а другой — в точке P на плоскости. Если P находится на краю треугольника и примыкает к одному из его оснований, то P находится внутри внутреннего угла этого основания (измеряемого от центра до края). Но если P лежит вне одного или обоих оснований, то оно попадает в пределы одного или нескольких их внешних углов (измеряемых от края до противоположной вершины).
В этом случае P находится внутри внешнего угла основания B в точке Q; но поскольку Q лежит вне обоих оснований, оно также попадает во внутренний угол B (в R), а также во внешний угол C (в S).
Leave A Comment