Найти уравнение с наименьшим корнем 4 класс: Найдите уравнение с наименьшим корнем. x*4=480/2 X*4=480*2 X*3=480*2 Придумайте задачу к этому уравнению?

Как решать квадратные уравнения? Формулы и Примеры

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, которое содержит переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.

А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

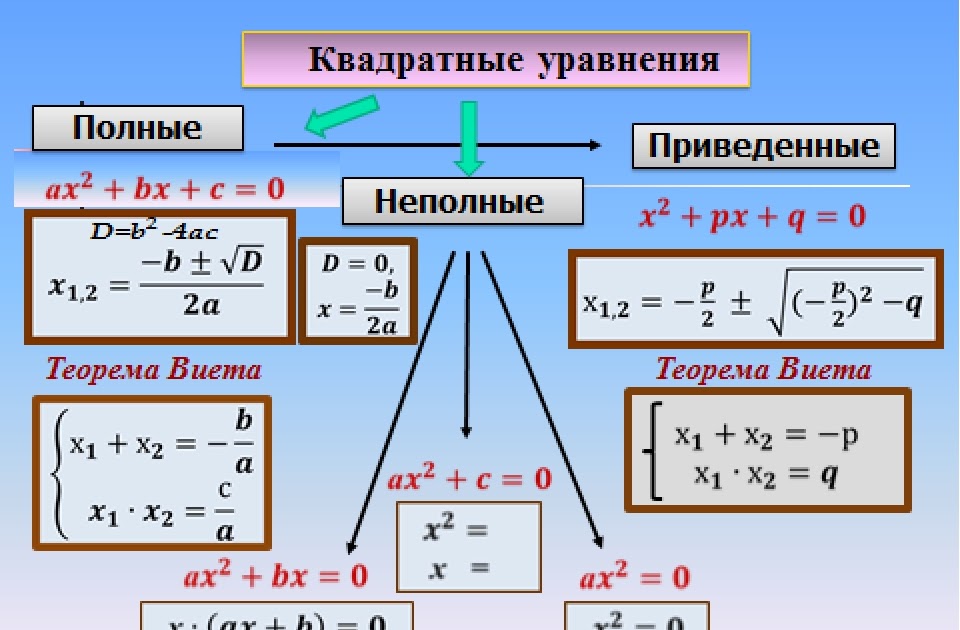
Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.

Квадратные уравнения могут иметь два корня, один корень или не иметь корней.

Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта:

если D < 0, корней нет;
если D = 0, есть один корень;
если D > 0, есть два различных корня.

С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.

Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Приведенные и неприведенные квадратные уравнения

Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.

Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.

Давайте-ка на примерах — вот у нас есть два уравнения:

x² — 2x + 6 = 0
x² — x — 1/4 = 0

В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x² ), а значит уравнение называется приведенным.

2x² − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.

Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Запоминаем!

У преобразованного уравнения те же корни, что и у первоначального. Ну или вообще нет корней.

Пример 1. Превратим неприведенное уравнение: 8x² + 20x — 9 = 0 — в приведенное.

Для этого разделим обе части исходного уравнения на старший коэффициент 8:

Ответ: равносильное данному приведенное уравнение x² + 2,5x — 1,125 = 0.

Пройдите тест и узнайте, какие темы отделяют от пятёрки по математике

Полные и неполные квадратные уравнения

В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax² + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.

Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.

Неполное квадратное уравнение —— это квадратное уравнение вида ax² + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.

Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.

Для самых любопытных объясняем откуда появились такие названия:
Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0. Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0. Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0. Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Для самых любопытных объясняем откуда появились такие названия:

Если b = 0, то квадратное уравнение принимает вид ax² + 0x+c=0 и оно равносильно ax² + c = 0.
Если c = 0, то квадратное уравнение выглядит так ax² + bx + 0 = 0, иначе его можно написать как ax² + bx = 0.

Если b = 0 и c = 0, то квадратное уравнение выглядит так ax² = 0.

Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

ax² = 0, ему отвечают коэффициенты b = 0 и c = 0;
ax² + c = 0, при b = 0;

ax² + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax

² = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0.

Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a

, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x² = 0.

Как решаем:

Замечаем, что данному уравнению равносильно x² = 0, значит исходное уравнение имеет единственный корень — нуль.
По шагам решение выглядит так:
−6x² = 0
x² = 0
x = √0
x = 0

Ответ: 0.

Как решить уравнение ax

² + с = 0

Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0:

перенесем c в правую часть: ax² = — c,
разделим обе части на a: x² = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и

c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а < 0, то уравнение x² = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.

Если — c/а > 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)

2 = — c/а. Ура, больше у этого уравнения нет корней.

В двух словах
Неполное квадратное уравнение ax² + c = 0 равносильно уравнению х²= -c/a, которое: не имеет корней при — c/а < 0; имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.

В двух словах

Неполное квадратное уравнение ax² + c = 0 равносильно уравнению х²= -c/a, которое:

не имеет корней при — c/а < 0;
имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.

Пример 1. Найти решение уравнения 8x² + 5 = 0.

Как решать:

Перенесем свободный член в правую часть:
8x² = — 5
Разделим обе части на 8:
x² = — 5/8
В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x² + 5 = 0 не имеет корней.

Как решить уравнение ax

² + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня:

x = 0;
x = −b/a.

Пример 1. Решить уравнение 0,5x² + 0,125x = 0

Как решать:

Вынести х за скобки
х(0,5x + 0,125) = 0
Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
Решить линейное уравнение:
0,5x = −0,125,
х = −0,125/0,5
Разделить:
х = −0,25
Значит корни исходного уравнения — 0 и −0,25.

Ответ: х = 0 и х = −0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена

Если x₁ и x₂ — корни квадратного трехчлена ax² + bx + c, то справедливо равенство ax² + bx + c = a (x − x₁) (x − x₂).

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b² − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

, .

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax² + bx + c = 0:

вычислить его значение дискриминанта по формуле D = b²−4ac;
если дискриминант отрицательный, зафиксировать, что действительных корней нет;
если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x² + 28x — 49 = 0.

Как решаем:

Найдем дискриминант: D = 28² — 4(-4)(-49) = 784 — 784 = 0
Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
Найдем корень
х = — 28/2(-4)
х = 3,5

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x² = 0.

Как решаем:

Произведем равносильные преобразования. Умножим обе части на −1
54 — 6x² = 0 | *(-1)
6x² — 54 = 0
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
6x² = 54
х² = 9
х = ±√9
х₁ = 3, х₂ = — 3

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x²— х = 0.

Как решаем:

Преобразуем уравнение так, чтобы появились множители
х(х — 1) = 0
х₁ = 0, х₂ = 1

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x²— 10 = 39.

Как решаем:

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
x²— 10 = 39
x²= 39 + 10
x²= 49
х = ±√49
х₁ = 7, х₂ = −7

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x²— 4x+94 = 0.

Как решаем:

Найдем дискриминант по формуле
D = (-4)² — 4 * 3 * 94 = 16 — 1128 = −1112
Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b² — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax² + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)²— 4ac = 4n² — 4ac = 4(n²— ac) и подставим в формулу корней:

Для удобства вычислений обозначим выражение n² -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n²— ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

вычислить D₁= n²— ac;
если D₁< 0, значит действительных корней нет;
если D₁= 0, значит можно вычислить единственный корень уравнения по формуле x = -n/a;
если же D₁> 0, значит можно найти два действительных корня по формуле

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Теорема Виета

Сумма корней x² + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x² + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x² + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x² + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x² + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x² + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Виета: x² − 6x + 8 = 0.

Как решаем:

Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.
Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:
Значит числа 4 и 2 — корни уравнения x² − 6x + 8 = 0. p>

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x² — 4 x — 6 = 0, чем 1100x² — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x² — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x²— 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x² — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x² + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x²— 3x + 7 = 0 перейти к решению 2x² + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

x₁ + x₂ = — b/a,
x₁* x₂ = c/a.

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x²— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

Показательные уравнения — как решать? Примеры, свойства и определение

Поможем понять и полюбить математику

Начать учиться

127.9K

Тех, кто умеет решать квадратные уравнения, не испугает, если одну из переменных нужно будет возвести в степень. Если же искомый x находится не в основании степени, а в ее показателе — значит, нам встретились показательные уравнения. Узнаем о них подробнее и рассмотрим примеры с решениями за 10 класс — они пригодятся на ЕГЭ.

Определение показательного уравнения

Показательными называются уравнения, в которых переменная находится в показателе степени. Простейшее уравнение такого вида: a^х = b, где a > 0, a ≠ 1 и a^x = a^y.

Для решения даже простейших показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс тему «Свойства степенной функции» — советуем повторить ее перед тем, как читать дальнейший материал.

Показательной функцией называют такую: y = a^x, где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a < 1 (но больше 0) — непрерывно убывает. Это хорошо видно на рисунке ниже.

Важно знать

Показательная функция не может быть отрицательным числом, т. е. выражение у = a^x при а ≤ 0 корней не имеет.

Свойства степеней

Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут решать сложные показательные уравнения.

a^m · aⁿ	a^m+n
a^m:aⁿ	a^m-n
(a · b)ⁿ	aⁿ · bⁿ
(a : b)ⁿ	aⁿ : bⁿ
(aⁿ)^m	a^{n · m}
a⁻ⁿ

Как видите, ничего нового здесь нет, все это проходят в 6–7 классе.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Методы решения показательных уравнений

Самые короткие и простые показательные уравнения решаются легко при помощи свойств степеней. Например:

4^х = 64.

Требуется найти, в какую степень нужно возвести 4, чтобы получить 64.

4 · 4 · 4 = 64

4³ = 64

4^x = 4³

Х = 3

Но как решать показательные уравнения вот такого вида: ? Нужно немного повозиться с преобразованием этого выражения. Например, сделать так, чтобы либо основания, либо степенные показатели стали одинаковы. Для этого мы можем разложить 128 и 4. Вы ведь заметили, что у них есть общий множитель? Правильно, это 2.

Теперь в нашем уравнении появились одинаковые основания, а значит, мы можем приравнять и степени.

В данном случае мы используем один из алгоритмов решения показательных уравнений — привели обе части равенства к одинаковым основаниям. Дальше рассмотрим и другие методы.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Приведение к одинаковому основанию

Весомую часть уравнений вида а^х = b (при а и b 0) можно решить, превратив b в определенную степень числа a. Именно это мы сделали в примере выше, получив одинаковые основания. Главная трудность в том, чтобы найти у этих чисел общее основание.

Если у нас есть одинаковые основания, но разные показатели степени, то при умножении чисел степени складываются, а при делении — вычитаются.

Пример 1

Рассмотрим еще одно показательное уравнение с корнем.

Мы знаем, что 64 и 8 являются степенями 2. Попробуем использовать это, и тогда 64² = 2¹², а 8 = 2³.

Ответ: .

Пример 2

В этом примере показательного уравнения нужно будет отдельно преобразовать каждую составляющую.

(0,5)^х2 · 4^х+1 = 64^-1

Найдем общее основание показательных функций:

0,5 = 1/2 = 2⁻¹

4 = 2²

64 = 2⁶

В результате у нас получается:

(2⁻¹)^х² · (2²)^х+1 = (2⁶)⁻¹

2^−х² · 2^2х+2 = 2⁻⁶

2^{−х²+2х+2} = 2⁻⁶

−х² + 2х + 2 = −6

х²− 2х − 8 = 0

Ответ: x = −2; 4.

Приведение к одинаковой степени

Не все показательные уравнения с разными основаниями можно решить предыдущим способом. Иногда проще преобразовать не основания, а показатели степени. Правда, пользоваться этим методом есть смысл только в том случае, когда мы имеем дело с умножением или делением.

При умножении чисел с разными основаниями, но одинаковыми степенными показателями можно перемножить только основания (степень останется прежней): a^xb^x = (ab)^x.

Пример

5^2х−4 = 49^2−х

Общих множителей у левой и правой части уравнения нет и привести их к одинаковому основанию достаточно трудно. Поэтому стоит поработать с показателями степеней:

5^2х−4 = 49^2−х

5^2х−4 = 7^4−2х

5^2х−4 = (1/7)^2х−4

35^2х−4 = 1

2х − 4 = 0

х = 2

Пример 2

2^х−2 = 5^2−х

Нам нужно привести обе части уравнения к одинаковым степенным показателям, и для этого вначале попробуем преобразовать правую часть, используя свойство степенных функций.

2^х−2 = 1/5^х−2

Теперь умножим обе части на 5^2−х и придем к уравнению:

2^х−2 × 5^2−х = 1

10^х−2 = 1

10^х−2 = 10⁰

х − 2 = 0

х = 2

Замена переменной

Суть этого способа решения показательных уравнений проста: мы заменяем «трудную» переменную на более простую и решаем уравнение, а после производим обратную замену. Главное — определить, какую именно переменную стоит заменить.

Пример

4^x— 2^x+1— 8 = 0

Очевидно, что в этом уравнении показательные функции легко привести к общему основанию: 4^х = 2^2х, а 2^х+1 = 2 × 2^х.

2^2х — 2 × 2^х — 8 = 0

Что-то напоминает. 🤔 Если бы из этого выражения можно было волшебным образом убрать 2^х, получилось бы обычное квадратное уравнение. Поэтому мы обозначим 2^х новой переменной — допустим, y.

Если 2^х = y, y > 0, то получается: у²— 2у — 8 = 0.

У такого уравнения есть два корня: у₁ = 4, у₂ = -2.

Проведем обратную замену: 2^х = 4 (подходит по ограничениям).

х = 2.

Ответ: х = 2.

Пример 2

25^х — 6 × 5^х + 5 = 0

Если присмотреться к этому выражению, становится понятно, что у него много общего с квадратным уравнением. Введем новую переменную: 5^х = у, y > 0.

у² — 6у + 5 = 0

Корни такого уравнения: 1 и 5.

Выполним обратную замену:

5^х = 1, значит х = 0.

5^х = 5, значит х = 1.

Ответ: x = 0; 1.

Вынесение общего множителя

В предыдущих примерах мы преобразовывали разные виды показательных уравнений путем разложения многочленов на множители, потому что хотели найти способ решения — получить одинаковые основания или выделить переменную, которую можно заменить.

Общий множитель — это некий многочлен, содержащий переменную, который в скрытом виде присутствует во всех показательных функциях уравнения. Его можно вынести за скобки, чтобы упростить уравнение.

Проблема только в том, чтобы научиться верно определять такое выражение, а этот навык появляется лишь с опытом.

Пример 1

3^х+1 + 3^х — 3^х-2 = 35

Вынесем 3^3-x за скобки и получим:

3^х-2(3³ + 3² — 1) = 35

3^х-2 × 35 = 35

3^х-2 = 1

Поскольку 1 равно любое число в нулевой степени, мы можем записать:

3^х-2 = 3⁰

х — 2 = 0

х = 2

Ответ: х = 2.

Пример 2

5 × 3^-3х+1 + 3^-3х+2 = 24

Для начала мы попробуем в левой части уравнения получить одинаковую степень: 3^-3х+2 = 3^-3х+1+1 = 3 · 3^-3х+1.

Теперь у нас есть общий множитель 3^-3х+1, который можно вынести за скобки, чтобы получить более простое уравнение:

3^-3х+1(5+3) = 24

8 · 3^-3х+1 = 24

3^-3х+1 = 3¹

-3х + 1 = 1

х = 0

Ответ: х = 0.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Яна Кононенко

К предыдущей статье

Показательные неравенства

К следующей статье

Параллельность прямых

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс

Поиск корней — Алгебра II

Все ресурсы по Алгебре II

10 Диагностических тестов 630 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 6 7 Следующая →

Алгебра II Помощь » Промежуточная алгебра с одной переменной » Квадратные уравнения и неравенства » Решение квадратных уравнений » Поиск корней

Умножьте приведенную выше функцию на множители, чтобы найти корни квадратного уравнения.

Возможные ответы:

Правильный ответ:

Объяснение:

Факторизация квадратного уравнения означает выполнение FOIL в обратном порядке. Вспомните, что когда вы используете FOIL, вы начинаете с двух двухчленов и заканчиваете трехчленом:

Теперь мы попытаемся пойти в другом направлении — начнем с трехчлена и вернемся к двум множителям.

Здесь -3 равно , а -2 равно . Мы можем использовать эту информацию, чтобы узнать, что такое и по отдельности. Другими словами, мы должны найти два множителя -3, которые в сумме дают -2.

Коэффициенты -3:

3*-1 (сумма = 2)
-3*1 (сумма = -2)

Таким образом, наше факторизованное уравнение должно выглядеть так:

Корнями квадратного уравнения являются значения x, для которых y равно 0.

Мы знаем, что все, что умножено на ноль, равно нулю. Таким образом, все выражение равно нулю, когда хотя бы один из множителей равен нулю.

Сообщить об ошибке

Найти корни функции:

Возможные ответы:

Правильный ответ:

Объяснение:

Фактор:

Двойная проверка по факторингу:

Добавить вместе:

Следовательно:

. Отчет.

Возможные ответы:

x = –5, –2

x = 4, 3

x = 5

x = 5, 2

x = –4, –3

Правильный ответ:

x = 5, 2

6 Пояснение:

1) Разделить средний член так, чтобы можно было разложить на множители путем группировки.

Факторы 10 включают:

1 * 10 = 10 1 + 10 = 11

2 * 5 = 10 2 + 5 = 7

–2 * –5 = 10 –2 + –5 = –7 Хорошо!

2) Теперь разложите по группам, вытащив «x» из первой пары и «-5» из второй.

3) Теперь вытяните общий множитель «(x-2)» из обоих членов.

4) Приравняйте оба члена к нулю, чтобы найти возможные корни и решить с помощью обратных операций.

x – 5 = 0, x = 5

x – 2 = 0, x = 2

Сообщить об ошибке

Найдите x.

Возможные ответы:

x = –5, –2

x = –4, 4

x = 2

x = 5, 2

4 x0 = –50016 Правильный ответ:
х = –4
Пояснение:
1) Первый шаг решения любого уравнения: объединить одинаковые члены. В квадратичных уравнениях проще всего приравнять выражение к нулю.
2) Есть два способа решить эту задачу. Первый и наиболее интуитивно понятный метод — стандартный факторинг.
16+1=17
8+2=10
4+4=8
4″ от второго.
4) Вытяните «(x+4)», чтобы получить:
5) Установите каждый член равным нулю.
х + 4 = 0, х = –4
Но есть короткий путь! Предполагая, что термины расположены в порядке убывания (т. е. ), а третий член является полным квадратом, квадратный корень которого равен половине среднего члена, математики используют небольшую хитрость. В этом случае квадратный корень из 16 равен 4. 4 * 2 = 8, так что трюк сработает. Возьмите квадратный корень из первого и последнего членов, затем вставьте знак плюс между ними и квадратные скобки.
И снова x равно -4.
Отчет о ошибке
Найдите корни уравнения x ² + 5 x + 6 = 0
Возможные ответы:
–2 и –3
1 и –3
4. –5 и 1
2 и 3
3 и –3
Правильный ответ:
–2 и –3
Объяснение:
Чтобы разложить это на множители, нам нужно найти пару чисел, которые умножаются на 6 и в сумме дают 5. Числа 2 и 3 работают. (2 * 3 = 6 и 2 + 3 = 5)
SO ( x + 2) ( x + 3) = 0
x = –2 или x = –3
Отчет о ошибке
Решайте уравнение:

Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить квадратное уравнение, , мы устанавливаем уравнение равным нулю, а затем факторизуем квадратное уравнение, . Поскольку эти выражения умножаются на 0, то должно быть так, что хотя бы одно из выражений равно 0. Итак, мы составим соответствующие уравнения и , чтобы получить ответы и .
Сообщить об ошибке
Решить для :
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить для , вам нужно изолировать его в одной части уравнения. Вы можете вычесть справа налево. Затем вы можете добавить 6 справа налево:
Затем вы можете вынести это квадратное уравнение, чтобы найти . Вам нужно определить, какие множители 8 дают в сумме минус 6:
Finally, you set each binomial equal to 0 and solve for :
Report an Error
Solve for :
Possible Answers:
Correct answer:
Объяснение:
Сообщить об ошибке
Решить для .
Возможные ответы:
Правильный ответ:
Объяснение:
Первый фактор уравнения. Найдите два числа, которые умножаются на 24 и в сумме дают -10. Эти цифры составляют -6 и -4:
Установите оба выражения, равные 0 и решают для x:
Отчет о ошибке
Решение для:
Возможные ответы:
Правильный ответ. :
Объяснение:
Чтобы разложить на множители, найдите два числа, сумма которых равна 5, и умножьте на 6.
Проверьте возможные множители 6:
1 * 6 = 6
1 + 6 = 7, поэтому они не работают.
2 * 3 = 6
2 + 3 = 5, так что это работает!
Затем вытяните общие делители первых двух членов, а затем вторых двух членов:
Приравняйте оба выражения к 0 и решите:

и
Сообщить об ошибке
← Предыдущая 1 2 3 4 5 6 7 Следующая →
Уведомление об авторских правах 630 практических тестов Вопрос дня Карточки Learn by Concept
Квадратные уравнения – формулы, методы и примеры
Квадратные уравнения представляют собой алгебраические выражения второй степени и имеют форму x ² + bx + c = 0. Термин «квадратичный» происходит от латинского слова «quadratus», означающего квадрат, который относится к тому факту, что переменная x в уравнении возведена в квадрат. Другими словами, квадратное уравнение — это «уравнение второй степени». Существует множество сценариев, в которых используется квадратное уравнение. Знаете ли вы, что когда ракета запускается, ее траектория описывается квадратным уравнением? Кроме того, квадратное уравнение имеет множество приложений в физике, технике, астрономии и т. д.
Квадратные уравнения имеют максимум два решения, которые могут быть действительными или комплексными числами. Эти два решения (значения x) также называются корнями квадратных уравнений и обозначаются как (α, β). Мы узнаем больше о корнях квадратного уравнения в нижеследующем содержании.
1. Что такое квадратное уравнение?
2. Корни квадратного уравнения
3. Квадратичная формула
4. Природа корней квадратного уравнения
5. Формулы, относящиеся к квадратным уравнениям
6. Методы решения квадратных уравнений
7. Решение квадратных уравнений методом факторизации
8. Способ заполнения квадрата
9. Построение квадратного уравнения
10. Квадратные уравнения, имеющие общие корни
11. Максимальное и минимальное значение квадратного выражения
12. Часто задаваемые вопросы о квадратных уравнениях
Что такое квадратное уравнение?
Квадратное уравнение является алгебраическим уравнением второй степени относительно x. Квадратное уравнение в стандартной форме имеет вид ax ² + bx + c = 0, где a и b — коэффициенты, x — переменная, а c — постоянный член. Важным условием того, чтобы уравнение было квадратным, является то, что коэффициент при x ² является ненулевым членом (a ≠ 0). Для записи квадратного уравнения в стандартной форме сначала записывается член x ², затем член x и, наконец, записывается постоянный член.
Далее, в реальных математических задачах квадратные уравнения представляются в разных формах: (x — 1)(x + 2) = 0, -x ² = -3x + 1, 5x(x + 3) = 12х, х ³ = х(х ² + х — 3). Все эти уравнения необходимо преобразовать в стандартную форму квадратного уравнения перед выполнением дальнейших операций.
Корни квадратного уравнения
Корни квадратного уравнения — это два значения x, полученные путем решения квадратного уравнения. Эти корни квадратного уравнения также называют нулями уравнения. Например, корни уравнения x ² — 3x — 4 = 0 равны x = -1 и x = 4, поскольку каждое из них удовлетворяет уравнению. т. е.
При x = -1, (-1) ² — 3(-1) — 4 = 1 + 3 — 4 = 0
При x = 4, (4) ² — 3(4) — 4 = 16 — 12 — 4 = 0
Существуют различные методы нахождения корней квадратного уравнения. Использование квадратичной формулы является одним из них.
Квадратичная формула
Квадратная формула — самый простой способ найти корни квадратного уравнения. Есть некоторые квадратные уравнения, которые нелегко разложить на множители, и здесь мы можем удобно использовать эту квадратную формулу, чтобы найти корни самым быстрым способом. Два корня в квадратной формуле представлены как одно выражение. Положительный знак и отрицательный знак могут быть альтернативно использованы для получения двух различных корней уравнения.
Квадратная формула: Корни квадратного уравнения ax ² + bx + c = 0 равны x = [-b ± √(b ² — 4ac)]/2a.
Эта формула также известна как формула Шридхарачарьи.
Пример: Найдем корни того же уравнения, которое упоминалось в предыдущем разделе x ² — 3x — 4 = 0, используя квадратичную формулу.
а = 1, б = -3 и с = -4.
х = [-b ± √(b ² — 4ас)]/2а
= [-(-3) ± √((-3) ² — 4(1)(-4))]/2(1)
= [3 ± √25] / 2
= [3 ± 5] / 2
= (3 + 5)/2 или (3 — 5)/2
= 8/2 или -2/2
= 4 или -1 являются корнями.
Доказательство квадратной формулы
Рассмотрим произвольное квадратное уравнение: ax ² + bx + c = 0, a ≠ 0
Для определения корней этого уравнения поступим следующим образом:
ax ² + bx = -c ⇒ x ² + bx/a = -c/a
Теперь представим левую часть в виде полного квадрата, введя новый член (b/2a) ² с обеих сторон:
x ² + bx/a + (b/2a) ² = -c/a + (b/2a) ²
Левая часть теперь представляет собой полный квадрат:
(x + b/2a) ² = -c/a + b ²/4a ² ⇒ (x + b/2a) ² = (b ² — 4ac)/4a ²
Это хорошо для нас, потому что теперь мы можем извлекать квадратные корни, чтобы получить:
x + b/2a = ±√(b ² — 4ac)/2a
x = (-b ± √(b ² — 4ac))/2a
Таким образом, заполнив квадраты, мы удалось выделить x и получить два корня уравнения.
Природа корней квадратного уравнения
Корни квадратного уравнения обычно представляются символами альфа (α) и бета (β). Здесь мы узнаем больше о том, как найти природу корней квадратного уравнения без фактического нахождения корней уравнения.
Природа корней квадратного уравнения может быть найдена без фактического нахождения корней (α, β) уравнения. Это возможно, взяв значение дискриминанта, которое является частью формулы для решения квадратного уравнения. Значение b ² — 4ac называется дискриминантом квадратного уравнения и обозначается буквой ‘D’. На основе значения дискриминанта можно предсказать характер корней квадратного уравнения.
Дискриминант: D = b
² — 4ac
D > 0, корни действительны и различны
D = 0, корни вещественные и равные.
D < 0, корни не существуют или корни мнимые.
Теперь проверьте формулы, чтобы найти сумму и произведение корней уравнения.
Сумма и произведение корней квадратного уравнения
Коэффициент при x ² , член x и постоянный член квадратного уравнения ax ² ^{+ bx + c = 0 полезны при определении суммы и произведения корней квадратного уравнения. Сумма и произведение корней квадратного уравнения могут быть вычислены непосредственно из уравнения, без фактического нахождения корней квадратного уравнения. Для квадратного уравнения ax ² + bx + c = 0 сумма и произведение корней следующие.}
Сумма корней: α + β = -b/a = — Коэффициент x/ Коэффициент x ²
Произведение корней: αβ = c/a = постоянный член/ коэффициент x ²
Написание квадратных уравнений с использованием корней
Квадратное уравнение также может быть составлено для заданных корней уравнения. Если α, β являются корнями квадратного уравнения, то квадратное уравнение выглядит следующим образом.
x ² — (α + β)x + αβ = 0
Пример: Какое квадратное уравнение имеет корни 4 и -1?
Решение: Дано, что α = 4 и β = -1. Соответствующее квадратное уравнение находится по формуле:
x ² — (α + β)x + αβ = 0
х ² — (α + β)x + αβ = 0
х ² — (4 — 1)х + (4)(-1) = 0
х ² — 3х — 4 = 0
Формулы, относящиеся к квадратным уравнениям
Следующий список важных формул полезен для решения квадратных уравнений.
Квадратное уравнение в стандартной форме: ax ² + bx + c = 0
Дискриминант квадратного уравнения равен D = b ² — 4ac
При D > 0 корни действительны и различны.
При D = 0 корни действительны и равны.
При D < 0 действительные корни не существуют или корни мнимые.
Формула для нахождения корней квадратного уравнения: x = [-b ± √(b ² — 4ас)]/2а.
Сумма корней квадратного уравнения равна α + β = -b/a.
Произведение корня квадратного уравнения равно αβ = c/a.
Квадратное уравнение, корни которого равны α, β, равно x ² — (α + β)x + αβ = 0,
Условие для квадратных уравнений0778 = 0, имея одинаковые корни (A ₁ B ₂ — A ₂ B ₁) (B ₁ C ₂ — B _{2 _{1 _{1 _{) 1 _{) 1 _{) 1 _{) 1 _{) 1 _{) 1 _{1 _{1 _{1 _{1 _{1 _{1 _{1 _{1 _{1 _{1 _{1 _{1 _{). 2} c ₁ — a ₁ c ₂ ) ² .}}}}}}}}}}}}}}}}}}}}}
Когда a > 0, квадратное выражение f(x) = ax ² + bx + c имеет минимальное значение при x = -b/2a.
Когда a < 0, квадратное выражение f(x) = ax ² + bx + c имеет максимальное значение при x = -b/2a.
Область определения любой квадратичной функции — это множество всех действительных чисел.
Методы решения квадратных уравнений
Можно решить квадратное уравнение, чтобы получить два значения x или два корня уравнения. Существует четыре различных метода нахождения корней квадратного уравнения. Четыре метода решения квадратных уравнений заключаются в следующем.
Факторизация квадратного уравнения
Используя квадратичную формулу (которую мы уже видели)
Метод завершения квадрата
Графический метод поиска корней
Давайте подробно рассмотрим каждый из вышеперечисленных методов, чтобы понять, как использовать эти методы, их приложения и способы их использования.
Решение квадратных уравнений методом факторизации
Факторизация квадратного уравнения выполняется в несколько этапов. Для общей формы квадратного уравнения ax ² + bx + c = 0, нам нужно сначала разбить средний член на два члена так, чтобы произведение членов было равно постоянному члену. Далее мы можем взять общие члены из имеющегося члена, чтобы окончательно получить искомые коэффициенты следующим образом:
x ² + (a + b)x + ab = 0
x ² + топор + bx + ab = 0
х(х + а) + б(х + а)
(х + а) (х + б) = 0
Вот пример для понимания процесса факторизации.
х ² + 5х + 6 = 0
х ² + 2х + 3х + 6 = 0
х(х + 2) + 3(х + 2) = 0
(х + 2)(х + 3) = 0
Таким образом, два полученных множителя квадратного уравнения равны (x + 2) и (x + 3). Чтобы найти его корни, просто установите каждый множитель равным нулю и найдите x. т. е. x + 2 = 0 и x + 3 = 0, что дает x = -2 и x = -3. Таким образом, x = -2 и x = -3 являются корнями x ² + 5x + 6 = 0.
Далее, есть еще один важный метод решения квадратного уравнения. Метод заполнения квадрата квадратного уравнения также полезен для нахождения корней уравнения.
Метод завершения квадрата
Метод завершения квадратного уравнения заключается в алгебраическом возведении в квадрат и упрощении для получения требуемых корней уравнения. Рассмотрим квадратное уравнение ax ² + bx + c = 0, a ≠ 0. Чтобы определить корни этого уравнения, упростим его следующим образом:
ax ² + bx + c = 0
топор ² + Ьх = -с
x ² + bx/a = -c/a
Теперь представим левую часть в виде полного квадрата, введя новый член (b/2a) ² с обеих сторон:
x ² + bx/a + (b/2a) ² = -к/а + (б/2а) ²
(х + b/2а) ² = -с/а + b ² /4а ²
(x + b/2a) ² = (b ² — 4ac)/4a ²
х + b/2а = + √(b ² — 4ас)/2а
х = — б/2а + √(б ² — 4ас)/2а
х = [-b ± √(b ² — 4ac)]/2a
Здесь знак «+» соответствует одному корню, а знак «-» соответствует другому корню квадратного уравнения. Как правило, этого подробного метода избегают, и для получения требуемых корней используется только квадратичная формула.
Графическое изображение квадратного уравнения
График квадратного уравнения ax ² + bx + c = 0 можно получить, представив квадратное уравнение как функцию y = ax ² + бх + в. Далее, решая и подставляя значения для x, мы можем получить значения y, мы можем получить множество точек. Эти точки можно представить на оси координат, чтобы получить график в форме параболы для квадратного уравнения. Для получения подробной информации о построении графика квадратичной функции нажмите здесь.
Точки, в которых график пересекает горизонтальную ось х (обычно точки пересечения х), являются решением квадратного уравнения. Эти точки также можно получить алгебраически, приравняв значение y к 0 в функции y = ax ² + bx + c и решение для x.
Квадратные уравнения, имеющие общие корни
Рассмотрим два квадратных уравнения, имеющих общие корни a ₁ x ² + b ₁ x + c ₁ = 0 и = 0. Решим эти два уравнения, чтобы найти условия, при которых эти уравнения имеют общий корень. Два уравнения решаются относительно x ² и x соответственно.
(x ²) (B ₁ C ₂ — B ₂ C ₁) = (-x)/(A ₁ C _{2 _{777777777777777777777777777777777777777777777777777777 — A ₁ C _{7 — A ₁ C _{7 — A ₁ C _{7 — A ₁ C _{7 — A ₁ C _{7 — A ₁ C _{2 _{7 — A}) = 1/(A ₁ B ₂ — A ₂ B ₁)}}}}}}}}
x
6 2 = (B ₁ C _{2 = (B ₁ C _{2 — B ₁ C _{2 — B ₁ C} — B _C — B ₁ C} — B ₁ C} — B ₁ C — B ₁. / (а ₁ б ₂ — а ₂ б ₁ )
х = (а ₂ в ₁ — а ₁0778 ) / (a ₁ b ₂ — a ₂ b ₁ )
Следовательно, упрощая два приведенных выше выражения, мы получаем следующее условие для двух уравнений, имеющих общий корень.
(a ₁ b ₂ — a ₂ b ₁ ) (b ₁ c ₂ — b ₂ c ₁ ) = (a ₂ c ₁ — а ₁ в ₂ ) ²
Максимальное и минимальное значение квадратного выражения
Максимальное и минимальное значения квадратичной функции F(x) = ax ² + bx + c можно увидеть на графиках ниже. При положительных значениях a (a > 0) квадратное выражение имеет минимальное значение при x = -b/2a, а при отрицательном значении a (a < 0) квадратное выражение имеет максимальное значение при x = -b /2а. x = -b/2a — координата x вершины параболы.
Максимальное и минимальное значения квадратного выражения помогают найти диапазон квадратного выражения: Диапазон квадратного выражения также зависит от значения a. Для положительных значений a(a > 0) диапазон составляет [ F(-b/2a), ∞), а для отрицательных значений a ( a < 0) диапазон составляет (-∞, F(-b/ 2а)].
Для a > 0 Диапазон: [ f(-b/2a), ∞)
Для a < 0, диапазон: (-∞, f(-b/2a)]
Обратите внимание, что областью определения квадратичной функции является множество всех действительных чисел, т. е. (-∞, ∞).
Советы и рекомендации по квадратным уравнениям:
Некоторые из приведенных ниже советов и рекомендаций по квадратным уравнениям помогают упростить решение квадратных уравнений.
Квадратные уравнения обычно решаются с помощью факторизации. Но в случаях, когда она не может быть решена факторизацией, используется квадратичная формула.
Корни квадратного уравнения также называют нулями уравнения.
Для квадратных уравнений с отрицательными значениями дискриминанта корни представлены комплексными числами.
Сумму и произведение корней квадратного уравнения можно использовать для нахождения высших алгебраических выражений, включающих эти корни.
☛Похожие темы:
Калькулятор корней
Калькулятор квадратичного факторинга
Калькулятор корней квадратного уравнения

Примеры квадратных уравнений
Пример 1: Джеймс занимается фитнесом и каждое утро ходит на пробежку. Парк, в котором он бегает, имеет прямоугольную форму и имеет размеры 12 х 8 м. Группа защитников окружающей среды планирует обновить парк и решает построить дорожку вокруг парка. Это позволит увеличить общую площадь до 140 кв.м. Какова будет ширина дорожки?
Решение:
Обозначим ширину пути через x.
Тогда длина и ширина внешнего прямоугольника равны (12+2x) м и (8+2x) м.
Учитывая, что площадь = 140
(12 + 2x)(8 + 2x) = 140
2(6 + x) 2(4 + x) = 140
(6 + x)(4 + x) = 35
24 + 6х + 4х + х ² = 35
х ² + 10х -11 = 0
х ² + 11х — х — х — 900 = 0 (01 х — 900) — 1(х + 11) = 0
(x + 11)(x — 1) = 0
(x + 11) = 0 и (x — 1) = 0
x = -11 и x = 1
Так как длина не может быть отрицательной , возьмем x = 1.
Ответ: Следовательно, ширина дорожки равна 1 м.
Пример 2: Рита бросает мяч вверх с платформы, находящейся на высоте 20 м над землей. Высота мяча над землей в момент времени «t» обозначается буквой «h». Предположим, что h = -4t ² + 16t + 20. Найдите максимальную высоту, на которую поднялся мяч.
Решение:
Члены квадратного уравнения
h = -4t ² + 16t + 20
можно переставить так, чтобы было легко найти максимальное значение этого уравнения.
h = -4t ² + 16t + 20
= -4t ² + 16t + 20
= -4(t ² — 4t — 5)
5 — 90 ) ² — 9)
= -4(t — 2) ² + 36
Мы должны сохранить значение (t — 2) ² минимум, чтобы найти максимальное значение h.
Итак, минимальное значение (t — 2) ² равно 0.
Ответ: Следовательно, максимальная достигнутая высота равна 36 м.
Пример 3: Найдите квадратное уравнение, имеющее корни 5 и 8 соответственно.
Решение:
Квадратное уравнение с корнями α, β равно x ² — (α + β)x + αβ = 0,
При α = 5 и β = 8.
Следовательно, квадратное уравнение:
x ² — (5 + 8)x + 5×8 = 0
Ответ: Следовательно, искомое квадратное уравнение равно x ² — 13x + 40 = 0
Пример 4: Квадратное уравнение 2x ² + 9x + 7 = 0 имеет корни α, β. Найдите квадратное уравнение, имеющее корни 1/α и 1/β.
Решение:
Метод 1:
Квадратное уравнение, корни которого обратны корням уравнения ax ² + bx + c = 0, равно cx ² + bx + a = 0,
заданное квадратное уравнение равно 2x ² + 9x + 7 = 0,
Следовательно, искомое уравнение, имеющее обратные корни, равно 7x ² + 9x + 2 = 0,
Метод 2: Из данного уравнения
5
45
4 α + β = -9/2 и α β = 2/7.
Корни нового уравнения должны быть 1/α и 1/β.
Их сумма = 1/α + 1/β = (α + β) / α β = -9/7
Их произведение = 1/α β = 2/7
Таким образом, искомое уравнение:
х ² — (1/α + 1/β)x + 1/α β = 0
х ² — (-9/7)х + 2/7 = 0
Умножение обеих сторон на 7,
7x ² + 9x + 2 = 0
Ответ: Следовательно, уравнение 7x ² + 9x + 2 = 0,
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по квадратному уравнению

перейти к слайдуперейти к слайду
Часто задаваемые вопросы о квадратном уравнении
Что такое определение квадратного уравнения?
A квадратное уравнение в математике представляет собой уравнение второй степени вида ax ² + bx + c = 0. Здесь a и b — коэффициенты, c — постоянный член, а x — переменная. Поскольку переменная x имеет вторую степень, у этого квадратного уравнения есть два корня или ответа. Корни квадратного уравнения можно найти либо путем факторизации, либо с помощью квадратной формулы.
Что такое квадратичная формула?
Формула квадратного уравнения для решения уравнения оси ² + bx + c = 0 равно x = [-b ± √(b ² — 4ac)]/2a. Здесь мы получаем два значения x, применяя символы плюс и минус в этой формуле. Отсюда два возможных значения x: [-b + √(b ² — 4ac)]/2a и [-b — √(b ² — 4ac)]/2a.
Как решить квадратное уравнение?
Существует несколько методов решения квадратных уравнений, но наиболее распространенными из них являются разложение на множители, использование квадратной формулы и завершение квадрата.
Факторинг включает в себя нахождение двух чисел, которые умножаются на постоянный член c и в сумме дают коэффициент x, b.
Квадратичная формула используется, когда факторизация невозможна, и задается как x = [-b ± √(b ² — 4ac)]/2a.
Чтобы составить квадрат, нужно переписать квадратное уравнение в другой форме, которая позволяет легко найти x.
Что такое определитель в квадратичной формуле?
Значение б ² — 4ac называется дискриминантом и обозначается буквой D. Дискриминант является частью квадратичной формулы. Дискриминанты помогают нам найти природу корней квадратного уравнения, фактически не находя корней квадратного уравнения.
Каковы некоторые реальные приложения квадратных уравнений?
Квадратные уравнения используются для нахождения нулей параболы и ее оси симметрии. Есть много реальных приложений квадратных уравнений.
Их можно использовать в задачах на время бега для оценки скорости, расстояния или времени во время путешествия на машине, поезде или самолете.
Квадратные уравнения описывают взаимосвязь между количеством и ценой товара.
Точно так же расчеты спроса и затрат также считаются задачами квадратного уравнения.
Также можно отметить, что форма спутниковой антенны или телескопа-рефлектора определяется квадратным уравнением.
Чем квадратные уравнения отличаются от линейных уравнений?
Линейная степень — это уравнение одной степени и одной переменной, а квадратное уравнение — это уравнение двух степеней и одной переменной. Линейное уравнение имеет вид ax + b = 0, а квадратное уравнение имеет вид ax ² + bx + c = 0. Линейное уравнение имеет один корень, а квадратное уравнение имеет два корня или два ответа. Кроме того, квадратное уравнение является произведением двух линейных уравнений.
Каковы 4 способа решения квадратного уравнения?
Ниже приведены четыре способа решения квадратного уравнения.
Метод факторизации
Метод вычисления корней квадратного уравнения
Способ заполнения квадратов
Графический метод
Как решить квадратное уравнение, составив квадрат?
Квадратное уравнение решается методом завершения квадрата по формуле (a + b)^2 = a 92 = а ² — 2аб + б ² .
Как найти значение дискриминанта?
Значение дискриминанта в квадратном уравнении можно найти из переменных и постоянных членов стандартной формы квадратного уравнения ax ² + bx + c = 0. Значение дискриминанта D = b ² — 4ac, и это помогает предсказать природу корней квадратного уравнения, фактически не находя корней уравнения.
Как решать квадратные уравнения с помощью графиков?
Квадратное уравнение можно решить аналогично линейному равенству с помощью графика. Возьмем квадратное уравнение ax ² + bx + c = 0 в виде y = ax ² + bx + c . Здесь мы берем набор значений x и y и строим график. Две точки, где этот график встречается с осью x, являются решениями этого квадратного уравнения.
Насколько важен дискриминант квадратного уравнения?
Дискриминант очень нужен, чтобы легко найти природу корней квадратного уравнения. Без дискриминанта нахождение природы корней уравнения — долгий процесс, так как сначала нужно решить уравнение, чтобы найти оба корня. Следовательно, дискриминант является важной и необходимой величиной, которая помогает легко найти природу корней квадратного уравнения.
Где найти программу решения квадратных уравнений?
Чтобы получить программу решения квадратных уравнений, нажмите здесь. Здесь мы можем ввести значения a, b и c для квадратного уравнения ax ² + bx + c = 0, тогда оно даст вам корни вместе с пошаговой процедурой.
Какая польза от дискриминантов в квадратичной формуле?
Дискриминант (D = b ² — 4ac) полезен для предсказания природы корней квадратного уравнения. При D > 0 корни действительны и различны, при D = 0 корни действительны и равны, а при D < 0 корни не существуют или являются мнимыми комплексными числами. С помощью этого дискриминанта и с наименьшими вычислениями мы можем найти природу корней квадратного уравнения.
Как решить квадратное уравнение, не используя квадратную формулу?
Существует два альтернативных метода квадратичной формулы.