Вписанная в ромб окружность | Треугольники

Какими свойствами обладает вписанная в ромб окружность? Как найти её радиус?

Центр вписанной в ромб окружности — точка пересечения его диагоналей.

Радиус вписанной в ромб окружности можно найти по общей формуле

   

где S — площадь ромба, p — его полупериметр.

Так как полупериметр ромба равен p=2a, где a — сторона ромба, эту формулу можно записать как

   

С учётом формул для нахождения площади ромба:

   

где α — угол ромба (причем α может быть как острым, так и тупым).

   

где d1и d2 — диагонали ромба.

Таким образом, еще две формулы радиуса вписанной в ромб окружности:

   

   

Так как диаметр вписанной окружности равен высоте ромба, радиус равен половине высоты ромба:

   

Если известно, что точка касания вписанной окружности делит сторону ромба на отрезки, то радиус можно выразить через длины этих отрезков.

Так как диагонали ромба взаимно перпендикулярны и радиус, проведённый в точку касания, перпендикулярен стороне, то по свойству высоты прямоугольного треугольника из треугольника AOD имеем

   

Следовательно, радиус вписанной в ромб окружности есть среднее пропорциональное между отрезками, на которые делит сторону точка касания:

   

www.treugolniki.ru

Радиус вписанной окружности в ромб

Ромб – это параллелограмм, у которого все стороны равны. Следовательно, он наследует все свойства параллелограмма. А именно:


  • Диагонали ромба взаимно перпендикулярны.
  • Диагонали ромба являются биссектрисами его внутренних углов.

Окружность можно вписать в четырехугольник тогда и только тогда, когда суммы противоположных сторон равны.
Следовательно, в любой ромб можно вписать окружность. Центр вписанной окружности совпадает с центром пересечения диагоналей ромба.
Радиус вписанной окружности в ромб можно выразить несколькими способами

1 способ. Радиуса вписанной окружности в ромб через высоту

Высота ромба равна диаметру вписанной окружности. Это следует из свойства прямоугольника, который образуют диаметр вписанной окружности и высота ромба – у прямоугольника противолежащие стороны равны.

Следовательно формула радиуса вписанной окружности в ромб через высоту:

2 способ. Радиус вписанной окружности в ромб через диагонали

Площадь ромба можно выразить через радиус вписанной окружности

, где Р– периметр ромба. Зная, что периметр это сумма всех сторон четырехугольника имеем P=4×а. Тогда
Но площадь ромба  также равна половине произведения его диагоналей
Прировняв правые части формул площади, имеем следующее равенство
В результате получаем формулу, позволяющую вычислить радиус вписанной окружности в ромб чрез диагонали

Пример расчета радиуса окружности вписанной в ромб, если известны диагонали
Найти радиус окружности вписанной в ромб, если известно, что длина диагоналей 30 см и 40 см
Пусть ABCD-ромб, тогда AC и BD его диагонали. AC=30 см
, BD=40 см
Пусть точка О – это центр вписанной в ромб ABCD окружности, тогда она будет также являться и точкой пересечения его диагоналей, делящих их пополам.


т.к диагонали ромба пересекаются под прямым углом, то треугольник AOB прямоугольный. Тогда по теореме Пифагора
, подставляем в формулу ранее полученные значения

AB = 25 см
Применив ранее выведенную формулу для радиуса описанной окружности в ромб, получаем

3 способ. Радиус вписанной окружности в ромб через отрезки m и n

Точка F – точка касания окружности со стороной ромба, которая делит ее на отрезки AF и BF. Пусть AF=m, BF=n.
Точка O – центр пересечения диагоналей ромба и центр вписанной в него окружности.

Треугольник AOB – прямоугольный, так как диагонали ромба пересекаются под прямым углом.
, т.к. является радиусом, проведенным в точку касания окружности . Следовательно OF – высота треугольника AOB к гипотенузе. Тогда AF и BF – проекции катетов на гипотенузу.
Высота в прямоугольном треугольнике, опущенная на гипотенузу есть среднее пропорциональное между проекциями катетов на гипотенузу.

Формула радиуса вписанной окружности в ромб через отрезки равна корню квадратному из произведения этих отрезков, на которые делит сторону ромба точка касания окружности

Пример расчета радиуса окружности вписанной в ромб, если известны отрезки
m и n
Найдите радиус описанной окружности в ромб, если точка касания делит сторону ромба на 9 и 4
Пусть ABCD-ромб, тогда AC и BD его диагонали.
Пусть точка O – это центр вписанной в ромб ABCD окружности.
Пусть точка F – точка касания окружности со стороной ромбаAB. Тогда. AF=9, BF=4
Применив ранее полученную формулу, получаем

2mb.ru

Радиус вписанной окружности в ромб

1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

 

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

О — центр вписанной окружности

r — радиус вписанной окружности

 

Формула радиуса вписанной окружности в ромб через диагонали ( r ) :

 

 

Формула радиуса вписанной окружности в ромб через сторону и угол (

 r ) :

 

Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :

 

Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :

 

 

2. Радиус вписанной окружности ромба, равен половине его высоты

 

a — сторона ромба

h — высота

О — центр вписанной окружности

r — радиус вписанной окружности

 

Формула радиуса вписанной окружности в ромб ( r ) :

Подробности
Автор: Administrator

www-formula.ru

В ромб вписана окружность

Когда в условии задачи сказано, что в ромб вписана окружность, в ходе ее решения может быть использовано одно из следующих рассуждений.

Точка касания вписанной в ромб окружности делит его сторону на отрезки

В этом случае радиус ромба и его диагонали можно найти, используя соотношения в прямоугольном треугольнике.

Например, F — точка касания вписанной в ромб окружности — делит сторону AB на отрезки AF=m, FB=n. О — центр вписанной в ромб окружности — является точкой пересечения его диагоналей. Треугольник AOB — прямоугольный (так как диагонали ромба взаимно перпендикулярны).

   

   

— как радиус, проведенный в точку касания. Значит, OF — высота, проведенная к гипотенузе. Отсюда

   

   

   

Высота ромба через радиус вписанной окружности

   

Радиус вписанной в ромб окружности

Радиус вписанной окружности можно найти по формуле

   

S — площадь ромба, p — его полупериметр (p=2a, где a — сторона ромба).

Соответственно, площадь ромба через радиус вписанной в него окружности

   

Поскольку площадь ромба также равна

   

   

   

Площадь ромба через отрезки, на которые делит сторону ромба точка касания вписанной в него окружности, может быть найдена как

   

 

 

www.uznateshe.ru

Радиус вписанной окружности в ромб

Радиус вписанной окружности в ромб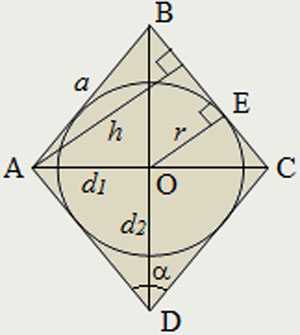

Существует свойство окружности, которую можно вписать в четырехугольник. Для этого должно выполняться всего одно условие: сумма одной пары противоположных сторон должна быть равна сумме другой пары противоположных сторон.
Поскольку для ромба это условие выполняется, то окружность можно вписать в любой ромб. Центр вписанной окружности и точка пересечения диагоналей ромба совпадают.
Рассмотрим несколько способов вычисления радиуса вписанной в ромб окружности

 
1 вариант. Вычислить радиус вписанной окружности через высоту.
Поскольку высота ромба и диаметр вписанной окружности равны, что следует из свойств прямоугольника, образованного диаметром вписанной окружности и высотой ромба.
Запишем формулу радиуса вписанной окружности:

   

 
2 вариант. Вычислить радиус вписанной окружности через диагонали.
Рассмотрим формулу площади ромба через радиус вписанной окружности:

   

   

   

С другой стороны площадь ромба можно найти через диагонали:

   

Приравняем правые части записанных формул площадей и получим:

   

Из этого равенства выразим радиус:

   

 

ru.solverbook.com

Как вписать окружность в ромб

Окружность можно вписать только в четырехугольник, у которого равны суммы противоположных сторон. Ромб этому условию соответствует, поскольку он представляет собой четырехугольник, у которого все стороны равны. Кроме того, они попарно параллельны, и это важно для требуемого построения. В ромб с заданными параметрами можно вписать всего одну окружность.

Вам понадобится

  • — лист бумаги;
  • — карандаш;
  • — циркуль;
  • — транспортир;
  • — компьютер с программой АutoCAD;
  • — калькулятор.

Инструкция

  • Начертите ромб с заданными параметрами. Вам должны быть известны длина стороны и хотя бы один угол. Сделать это можно как в обычной школьной тетради в клеточку, так и на компьютере. Для приблизительного рисунка, предназначенного, например, для презентации, подойдет даже программа Word с функцией рисования. Но в этой программе вы сможете передать только общий вид, без расчетов. Поэтому чертите в программе AutoCAD либо на листе бумаге проверенным за многие века способом. В первом случает найдите в меню функцию «Полигон». Выберите построение по длине стороны и ее положению. Введите количество сторон и угол.
  • При построении ромба на листе бумаги проведите горизонтальную линию, длина которой соответствует заданному размеру стороны. С помощью транспортира отложите от нее заданный угол и на поучившемся луче отложите тот же самый размер. Две другие стороны проведите параллельно уже имеющимся. Обозначьте ромб как АBCD.
  • Вспомните свойства ромба и вписанной в него окружности. В любом четырехугольнике, в который можно вписать окружность, центр ее лежит на пересечении биссектрис. В ромбе биссектрисы углов являются одновременно и диагоналями. То есть для того, чтобы найти центр окружности, необходимо их провести. Обозначьте центр окружности как О.
  • Вписанная окружность касается всех сторон многоугольника. То есть стороны ромба будут являться одновременно касательными. Вспомните свойство касательной. Она перпендикулярна радиусу, проведенному в точку касания. То есть необходимо провести из центра окружности перпендикуляр хотя бы к одной из его сторон. Поставьте точку N.
  • Поставьте иголку циркуля в точку О, Разведите его ножки на расстояние ON. Начертите окружность. Она будет иметь точки касания со всеми сторонами ромба.
  • Если необходимо вычислить величину радиуса вписанной окружности, сделайте это, применив различные формулы площади данной фигуры. S=a*h, где a – заданная в условии сторона, а h – высота. Высота ромба является одновременно удвоенным радиусом вписанной окружности, то есть формулу площади можно представить как S=2ar. В то же время, S=a2*sinα. Получается, что 2ar=a2*sinα. Найдите неизвестную величину r. Радиус равен частному от деления произведения квадрата стороны и синуса угла на удвоенную сторону. То есть r=a2*sinα/2a.
  • Вписанную окружность в программе АutoCAD постройте по уже известному вам центру и найденному радиусу. Для этого в главном меню найдите панель «Рисование». Найдите выпадающее окошко «Круг» и выберите «центр, радиус». Центр укажите с помощью курсора.

completerepair.ru

Как найти радиус окружности, вписанной в ромб

Автор КакПросто!

Параллелограмм, все стороны которого имеют одинаковую длину, называют ромбом. Это основное свойство определяет и равенство углов, лежащих в противоположных вершинах такой плоской геометрической фигуры. В ромб можно вписать окружность, радиус которой рассчитывается несколькими способами.

Статьи по теме:

Инструкция

Если известна площадь (S) ромба и длина его стороны (a), то для нахождения радиуса (r) вписанной в эту геометрическую фигуру окружности рассчитайте частное от деления площади на удвоенную длину стороны: r=S/(2*a). Например, если площадь равна 150 см², а длина стороны — 15 см, то радиус вписанной окружности будет равен 150/(2*15) = 5 см. Если кроме площади (S) ромба известна величина острого угла (α) в одной из его вершин, то для вычисления радиуса вписанной окружности найдите квадратный корень из четверти произведения площади на синус известного угла: r=√(S*sin(α)/4). Например, если площадь равна 150 см², а известный угол имеет величину 25°, то расчет радиуса вписанной окружности будет выглядеть так: √(150*sin(25°)/4) ≈ √(150*0,423/4) ≈ √15,8625 ≈ 3,983 см. Если известны длины обеих диагоналей ромба (b и c), то для вычисления радиуса вписанной в такой параллелограмм окружности найдите соотношение между произведением длин сторон и квадратным корнем из суммы их длин, возведенных в квадрат: r=b*c/√(b²+c²). Например, если диагонали имеют длину 10 и 15 см, то радиус вписанной окружности составит 10*15/√(10²+15²) = 150/√(100+225) = 150/√325 ≈ 150/18,028 ≈ 8,32 см.

Если известна длина лишь одной диагонали ромба (b), а также величина угла (α) в вершинах, которые соединяет эта диагональ, то для расчета радиуса вписанной окружности умножайте половину длины диагонали на синус половины известного угла: r=b*sin(α/2)/2. Например, если длина диагонали равна 20 см, а величина угла — 35°, то радиус будет рассчитываться так: 20*sin(35°/2)/2 ≈ 10*0,301 ≈ 3,01 см.

Если все углы в вершинах ромба равны, то радиус вписанной окружности всегда будет составлять половину длины стороны этой фигуры. Так как в евклидовой геометрии сумма углов четырехугольника равна 360°, то каждый угол будет равен 90°, а такой частный случай ромба будет являться квадратом.

Источники:

  • как найти радиус вписанной окружности в ромб

Совет полезен?

Распечатать

Как найти радиус окружности, вписанной в ромб

Статьи по теме:

Не получили ответ на свой вопрос?
Спросите нашего эксперта:

www.kakprosto.ru