| |||||||||||||||||||||||||||||||||||||||||
| Специальный поиск | |||||||||||||||||||||||||||||||||||||||||
|
Физика Теория вероятностей и мат. статистика Гидравлика Теор. механика Прикладн. механика Химия Электроника Витамины для ума |
Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты |
||||||||||||||||||||||||||||||||||||||||
сопротивлением воздуха пренебречь Задача 16010 Из пушки выпустили последовательно два снаряда со скоростью v0 = 250 м/с: первый — под углом θ1 = 60° к горизонту, второй — под углом θ2 = 45° (азимут один и тот же).
Задача 20255 Дальность полета тела, брошенного в горизонтальном направлении со скоростью v = 10 м/с, равна высоте бросания (l = h). Сопротивлением воздуха пренебречь. С какой высоты h брошено тело?
Задача 20259 Начальная скорость брошенного камня v0 = 10 м/с, а спустя δt = 0,50 с скорость камня v = 7,0 м/с. На какую максимальную высоту hmax над начальным уровнем поднимется камень? Сопротивлением воздуха пренебречь.
Задача 20262 Два тела брошены вертикально вверх с одинаковыми начальными скоростями v0 с интервалом времени δt одно после другого. Первое тело брошено с земли, а второе с балкона, расположенного на высоте h над точкой бросания первого тела.
Задача 40147 Тело, брошенное с высоты 250 вертикально вниз с начальной скоростью 20 м/с, погрузилось в землю на глубину 20 см. Определить среднюю силу сопротивления почвы, если масса тела равна 2 кг. Сопротивлением воздуха пренебречь.
Задача 40524 Снаряд, масса которого m = 10 кг, имел начальную скорость v = 800 м/с, направленную под углом α = 60° к горизонту. Через некоторое время после выстрела снаряд разорвался на два осколка. Один осколок массой m1 = 3 кг через время t0 = 30 c с момента выстрела имел скорость v1 = 600 м/с, направленную горизонтально. Определить скорость v
Задача 10999 Тело, брошенное вертикально вверх, находилось на одной и той же высоте h = 8,6 м два раза с интервалом Δt = 3 с. Пренебрегая сопротивлением воздуха, вычислить начальную скорость брошенного тела.
Задача 11021 Самолет, летевший на высоте h = 2940 м со скоростью v = 360 км/ч, сбросил бомбу. За какое время t до прохождения над целью и на каком расстоянии s от нее должен самолет сбросить бомбу, чтобы попасть в цель? Сопротивлением воздуха пренебречь.
Задача 11025 Пуля пущена с начальной скоростью v0 = 200 м/с под углом α = 60° к горизонту. Определить максимальную высоту Н подъема, дальность s полета и радиус R кривизны траектории пули в ее наивысшей точке.
Задача 11050 Тело массой m = 5 кг брошено под углом α = 30° к горизонту с начальной скоростью v0 = 20 м/с. Пренебрегая сопротивлением воздуха, найти: 1) импульс силы F, действующей на тело, за время его полета; 2) изменение Δp импульса тела за время полета.
Задача 11059 Ракета, масса которой М = 6 т, поднимается вертикально вверх. Двигатель ракеты развивает силу тяги F = 500 кН. Определить ускорение а ракеты и силу натяжения Т троса, свободно свисающего с ракеты, на расстоянии, равном 1/4 его длины от точки прикрепления троса. Масса m троса равна 10 кг. Силой сопротивления воздуха пренебречь.
Задача 11101 Тело массой m = 1 кг, брошенное с вышки в горизонтальном направлении со скоростью v0 = 20 м/с, через t = 3 с упало на землю.
Задача 11102 Камень брошен вверх под углом φ = 60° к плоскости горизонта. Кинетическая энергия Т0 камня в начальный момент времени равна 20 Дж. Определить кинетическую Т и потенциальную П энергии камня в высшей точке его траектории. Сопротивлением воздуха пренебречь.
Задача 26213 Ракета массой m0 = 10 кг стартует с вершины горы высотой h = 2 км и летит так, что газы все время выбрасываются горизонтально. Пренебрегая сопротивлением воздуха, подсчитать кинетическую энергию WK ракеты во время удара о землю. Скорость газов равна u = 300 м/с, расход топлива μ = 0,03m0 в секунду.
Задача 26248 Снаряд в верхней точке своей траектории на высоте Н = 2 км разорвался на два одинаковых осколка.
Задача 26570 Мяч брошен со скоростью 14 м/с под углом 44° к горизонту. Во время полета он упруго ударяется о вертикальную стену, расположенную перпендикулярно плоскости, в которой лежит траектория мяча, на расстоянии 6 м от места бросания. На каком расстоянии от стены упадет мяч? Сопротивлением воздуха пренебречь.
Задача 11230 Из пушки выпустили последовательно два снаряда со скоростью 587 м/с, первый — под углом 53° к горизонту, второй — под углом 15°. Пренебрегая сопротивлением воздуха, найти интервал времени между выстрелами, при котором снаряды столкнутся друг с другом.
Задача 11566 Аэростат массы m начал спускаться с постоянным ускорением w.
Задача 13350 Ракета, масса которой в начальный момент M = 300 г, начинает выбрасывать продукты сгорания с относительной скоростью u = 200 м/с. Расход горючего μ = 100 г/с. Пренебрегая сопротивлением воздуха и внешним силовым полем, определить: 1) за какой промежуток времени скорость ракеты станет равной v1 = 50 м/с; 2) скорость v2, которую достигнет ракета, если масса заряда m0 = 0,2 кг.
Задача 13353 Ракета поднимается с нулевой начальной скоростью вертикально вверх. Начальная масса ракеты m0 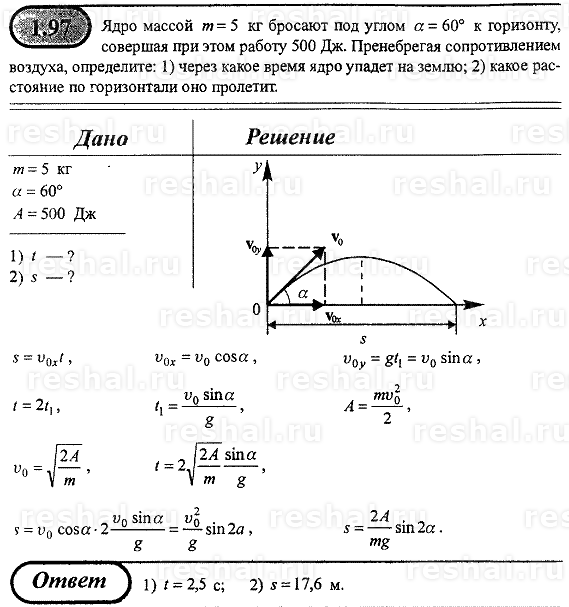 Поле силы тяжести считать однородным. Поле силы тяжести считать однородным.
Задача 13611 Камень, брошенный вертикально вверх с высоты h = 2 м со скоростью v0 = 20 м/с через какое-то время падает на землю. Найти среднюю скорость <v> его движения за последние 2,5 секунды полета. Сопротивлением воздуха пренебречь, ускорение свободного падения g = 9,815м/с2
Задача 14981 Из брандспойта бьёт струя воды под углом α = 35° к горизонту. Определите ежесекундный расход воды m (кг/с), если дальность полета струи равна S = 24 м, диаметр выходного отверстия брандспойта d = 2,2 см. Сопротивлением воздуха пренебречь.
Задача 15158 Груз, сброшенный с пикирующего самолета на высоте h на палубу корабля стоящего на рейде, имеет начальную скорость v0, направленную под углом α к вертикали.
Задача 15305 Пуля, вылетающая из горизонтально установленной винтовки, попадает точно в центр мишени, находящейся на расстоянии 200 м от винтовки. Мишень отодвинули на 20 м и опустили на 25 см. Определить на каком расстоянии от центра пуля попадет в мишень, выше или ниже центра? Начальная скорость пули при вылете из винтовки 600 м/с. Сопротивлением воздуха пренебречь.
Задача 15313 Тело брошено под углом 30° к горизонту. С какой скоростью было брошено тело и какова горизонтальная дальность его полета, если оно находилось в полете 2 с? Какова максимальная высота подъема тела? Сопротивлением воздуха пренебречь.
Задача 16101 Под каким углом α к горизонту нужно установить ствол орудия, чтобы поразить цель, находящуюся на расстоянии l = 10 км, если начальная скорость снаряда v0 = 500 м/с? Сопротивлением воздуха пренебречь.
Задача 17204 За время прыжка на высоту h = 4,9 м спортсмен на батуте сделал четыре оборота вокруг горизонтальной оси. Определить среднюю угловую скорость вращения спортсмена за время прыжка. Сопротивлением воздуха пренебречь.
Задача 17206 Снаряд имеет начальную скорость v = 3 км/с. На какую наибольшую высоту h может подняться снаряд? Сопротивлением воздуха пренебречь, учесть зависимость ускорения свободного падения от высоты.
Задача 17592 Небольшое тело, двигаясь с горизонтальной скоростью на высоте h, распалось на две части одинаковой массы. Одна часть упала на землю через время t1 прямо под местом распада. Вторая часть упала позднее. Сопротивлением воздуха пренебречь. Через какое время после распада вторая часть упала на землю?
Задача 17618 Человек бросает камень вертикально вниз с начальной скоростью 10 м/с с высоты 60 м.
Задача 19101 Тело, брошенное с высоты 5 м вертикально вниз со скоростью 20 м/с, погрузилось в грунт на глубину 20 см. Найти работу силы сопротивления грунта, если масса тела равна 2 кг. Сопротивлением воздуха пренебречь.
Задача 19271 Спортсмен на батуте за время прыжка на высоту h = 4,9 м сделал четыре оборота вокруг горизонтальной и два вокруг вертикальной осей. Определить среднюю угловую скорость вращения спортсмена за время прыжка. Какой угол с горизонталью образует вектор угловой скорости? Сопротивлением воздуха пренебречь.
Задача 20226 В магнитном поле с большой высоты падает с постоянной скоростью υ металлическое кольцо, имеющее диаметр d и сопротивление R.
Задача 20391 С какой скоростью нужно подбросить тело вертикально вверх, чтобы оно достигло высоты над поверхностью Земли, равной радиусу Земли? При расчете пренебречь сопротивлением воздуха, но учесть изменение силы тяжести.
Задача 20801 Пистолетная пуля пробила два вертикально расположенных листа бумаги, расстояние L между которыми равно 30 м. Пробоина во втором листе оказалась на h = 10 см ниже, чем в первом. Определить скорость V пули, если к первому листу она подлетела, двигаясь горизонтально. Сопротивлением воздуха пренебречь.
Задача 21530 Выстрел произведен из ружья, закрепленного горизонтально в южном полушарии на широте φ = 30°, по мишени, установленной севернее него.
Задача 21929 Камень бросили с крутого берега вверх под углом 30 градусов к горизонту со скоростью 10 м/с. С какой скоростью он упал в воду, если время полета 2 с. Сопротивлением воздуха пренебречь. Построить график скорости от времени и траекторию полета камня.
Задача 23149 Мяч, брошенный на высоте h0 = 80 см от поверхности земли под углом α = 30° к горизонту с начальной скоростью v0 = 12 м/с, пролетев в горизонтальном направлении расстояние L = 4 м, попадает в стенку на высоте h от поверхности земли. Найти эту высоту h. Сопротивлением воздуха пренебречь, ускорение свободного падения g = 9,815 м/с2.
Задача 23401 Сплошной цилиндр (1) и шар (2), имеющие одинаковые массы и радиусы, вкатываются без проскальзывания с одинаковыми начальными скоростями на горку. Найдите отношение высот h1/h2, на которые смогут подняться эти тела, если трением и сопротивлением воздуха можно пренебречь.
Задача 23599 С башни бросили тело со скоростью 20 м/с под углом 45° к горизонту. Тело упало на расстоянии 66 м от основания башни. Пренебрегая сопротивлением воздуха, найти: время движения тела; высоту башни; скорость тела в момент приземления.
Задача 23771 Скорость пули можно определить по понижению ее траектории Δh на заданном расстоянии l0 при горизонтальном выстреле (рис. 6.9). Рассчитайте скорость пули, считая l0, l и Δh известными и пренебрегая сопротивлением воздуха.
| |||||||||||||||||||||||||||||||||||||||||
Лобовое сопротивление воздуха подняло верхний конец вращающейся цепочки
Французские физики объяснили, почему конец замкнутой вращающейся цепочки самопроизвольно поднимается: оказалось, что этот эффект возникает из-за лобового сопротивления воздуха. Кроме того, ученые исследовали образование волн в такой цепочке и предложили измерять с их помощью силу натяжения. По словам исследователей, полученные результаты могут пригодиться на практике — например, при расчете движения шланга дозаправки самолетов. Статья опубликована в Physical Review Letters, кратко о ней сообщает Physics.
Хотя подвешенная цепочка (или веревка, что в каком-то приближении одно и то же) кажется очень простым объектом, в действительности с ней связанно множество интересных эффектов. Вероятно, самый необычный из них — это так называемый «фонтан из цепочки»: если сложить цепочку в стакан и выдернуть свободный конец, то она изогнется дугой и будет сохранять приобретенную форму, пока полностью не «выльется» из стакана. В сущности, складывать цепочку в стакан даже не обязательно, можно просто разложить ее на плоскости. Кроме того, ученые часто исследуют, как цепочка скатывается с гладкой поверхности — оказывается, что в некоторых случаях это движение также происходит парадоксальным образом. Например, если скатывающаяся цепочка изначально была сложена пополам, то в какой-то момент ускорение сложенного участка превысит ускорение свободного падения.
В сущности, складывать цепочку в стакан даже не обязательно, можно просто разложить ее на плоскости. Кроме того, ученые часто исследуют, как цепочка скатывается с гладкой поверхности — оказывается, что в некоторых случаях это движение также происходит парадоксальным образом. Например, если скатывающаяся цепочка изначально была сложена пополам, то в какой-то момент ускорение сложенного участка превысит ускорение свободного падения.
Более того, некоторые современные технологии полагаются на движение тонких и гибких объектов, — фактически тех же цепочек, погруженных в жидкость или газ. В частности, такую форму имеют ультразвуковой дальномер, с помощью которого корабль контролирует глубину дна, и шланг, с помощью которого самолет можно дозаправить в воздухе. Движение такого объекта определяется соотношением между силами гравитационного притяжения, сопротивления среды, натяжения кабеля и изгибных напряжений. В общем случае теоретически рассчитать поведение цепочки, помещенной в такие условия, довольно сложно.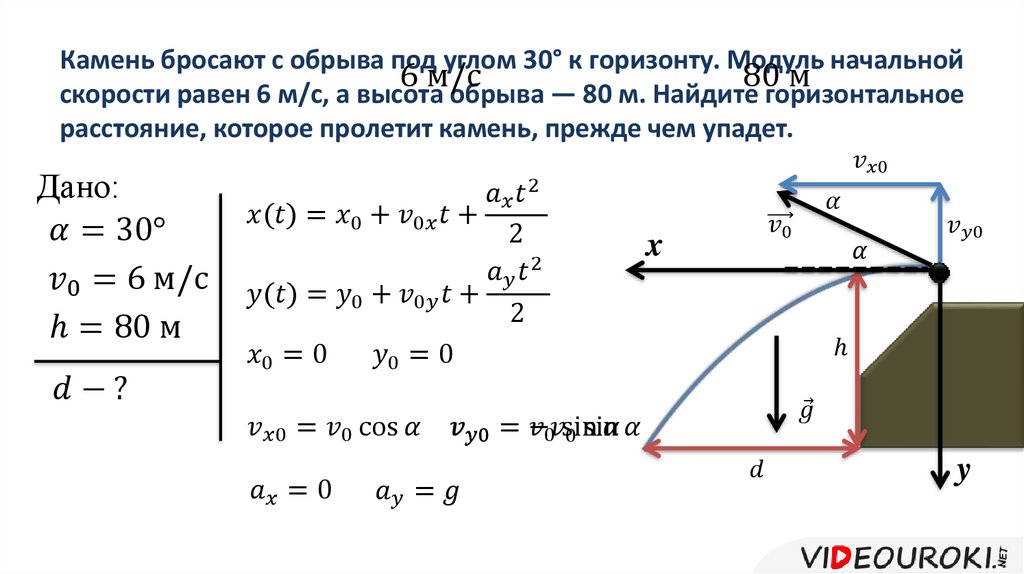
Поэтому группа физиков под руководством Николя Плиона (Nicolas Plihon) экспериментально исследовала движение цепочки в воздухе, и ухватила несколько общих закономерностей, которые ей управляют. Чтобы упростить задачу, ученые рассмотрели движение замкнутой цепочки, зажатой между вращающимися колесиками и разогнанной до постоянной скорости v (так как цепочка была почти нерастяжимой, модуль скорости всех ее точек совпадал). В качестве цепочки ученые выбирали тяжелые бусы или легкий хлопковый шнурок. Поскольку во время движения цепочка не покидает вертикальную плоскость, ее форму можно описать, задавая в каждой точке угол между бесконечно малым элементом цепочки и горизонталью. При этом естественно выделить точку, в которой цепочка поворачивает под углом 90 градусов к горизонтали (точка O на рисунке), и выделить в ней исходящую (кривая AO) и входящую (кривая OB) часть.
Очевидно, что движением цепочки управляет три силы — вес цепочки, тянущий ее вниз, сила натяжения, направленная вдоль цепочки, и лобовое сопротивление воздуха, направленное против движения цепочки. Ученые подчеркивают, что из-за симметрии задачи подъемной силой можно пренебречь. Также авторы отмечают, что натяжение цепочки удобно разбить на кинетический вклад, связанный с движением, и дополняющий его до полного натяжения эффективный вклад. С помощью этих обозначений уравнения движения можно свести к безразмерным величинам, с которыми гораздо удобнее работать.
Ученые подчеркивают, что из-за симметрии задачи подъемной силой можно пренебречь. Также авторы отмечают, что натяжение цепочки удобно разбить на кинетический вклад, связанный с движением, и дополняющий его до полного натяжения эффективный вклад. С помощью этих обозначений уравнения движения можно свести к безразмерным величинам, с которыми гораздо удобнее работать.
В зависимости от соотношения между двумя внешними силами — силой тяжести и силой сопротивления — физики выделили две принципиально разных ситуации. В первом случае, когда силой сопротивления воздуха можно было пренебречь, профиль шнурка практически не зависел от скорости и сводился к обыкновенной цепной линии. Единственное отличие этого случая от статического заключалось в том, что натяжение цепной линии сдвигалось на кинетическое натяжение.
Во втором же случае поведение шнурка было контринтуитивным: несмотря на отсутствие подъемной силы, конец цепочки начинал приподниматься, причем тем заметнее, чем выше была ее скорость.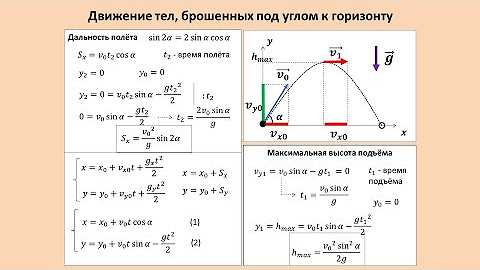 По словам ученых, это поведение можно объяснить сопротивлением воздуха, которое направлено вверх на правом участке цепочки, вертикально падающем вниз. Во-первых, это предположение согласуется с аналитическими и численными расчетами. Во-вторых, эффект полностью исчезает, когда из камеры откачивают воздух.
По словам ученых, это поведение можно объяснить сопротивлением воздуха, которое направлено вверх на правом участке цепочки, вертикально падающем вниз. Во-первых, это предположение согласуется с аналитическими и численными расчетами. Во-вторых, эффект полностью исчезает, когда из камеры откачивают воздух.
Кроме того, физики обнаружили, что из-за неоднородностей цепочки (например, узла, завязанного на шнурке) в ней самопроизвольно возбуждаются волны, движущиеся с переменной скоростью c(s)≈(T(s)/λ)½, где T(s) — полное натяжение цепочки, λ — ее линейная масса, а s — координата вдоль цепочки. В случае, когда натяжение цепочки слабо отличалось от кинетического натяжения, скорость волн практически совпадала со скоростью цепочки, поэтому для внешнего наблюдателя они выглядели как «медленные» волны (движущиеся вдоль кривой со скоростью v−c) и «быстрые» волны (со скоростью v+c). Впрочем, «быстрые» волны быстро добегали до края цепочки и отражались, превращаясь в «медленные». Интересно, что по скорости волн можно однозначно восстановить натяжение цепочки во всех ее точках. Авторы предполагают, что это замечание может пригодиться при работе с реальными «цепочками» — шлангами и канатами.
Интересно, что по скорости волн можно однозначно восстановить натяжение цепочки во всех ее точках. Авторы предполагают, что это замечание может пригодиться при работе с реальными «цепочками» — шлангами и канатами.
Вообще говоря, аэродинамические свойства часто проявляются даже в неожиданно простых эффектах. Например, в сентябре 2015 года физики из Университета Калифорнии и Технологического университета Шарифа (Иран) обнаружили, что закрученное кольцо, лежащее на столе, стремится вернуться в исходное положение, словно бумеранг. В то же время, монетка, помещенная в те же условия, такими свойствами не обладает. Этот эффект ученые списали на то, что монетку отделяет от поверхности небольшая прослойка «запертого» воздуха, тогда как у кольца такой прослойки нет. Это увеличивает силу трения и в какой-то момент заставляет кольцо повернуть обратно.
Дмитрий Трунин
Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.
ньютоновская механика — Можем ли мы игнорировать сопротивление воздуха?
$\begingroup$
Есть ли в реальной жизни случай, когда мы можем получить правильные (правильные) «уравнения движения» для объекта с игнорированием сопротивления воздуха? В любом состоянии объекта (размер или форма объекта, который мы изучаем).
- ньютоновская механика
- гидродинамика
- снаряд
- сопротивление
- приближения
$\endgroup$
7
$\begingroup$
Нет, вы не можете игнорировать его, если хотите получить точную информацию. На самом деле вам нужны точные измерения каждого отдельного атома в системе, чтобы быть абсолютно правильным. И даже в этом случае квантовая механика говорит, что вы будете правы только статистически.
Мы не пытаемся сделать все правильно. Мы даже не пытаемся. Что мы пытаемся сделать, так это сделать достаточно правильно, чтобы наши прогнозы были значимыми.
Во многих ситуациях прогнозы, которые вы делаете, игнорируя сопротивление воздуха, имеют большое значение. Они полезны до такой степени, что мы даже не учим реальному сопротивлению воздуха до тех пор, пока кто-нибудь не начнет карьеру физика.
$\endgroup$
$\begingroup$
Маятник является практическим примером, когда легко проверить точность игнорирования сопротивления воздуха.
Если вы измерите период колебаний $T = 2 \pi \sqrt {\frac{L}{g}}$ с помощью хронометра, погрешность измерения, вероятно, будет больше, чем суммарный эффект сопротивления воздуха и аппроксимация малый угол, используемый для формулы.
Неудивительно, что они так долго использовались для измерения времени.
$\endgroup$
$\begingroup$
Число Рейнольдса характеризует, насколько важны силы вязкости по отношению к силам инерции.
При более высоких числах Рейнольдса вязкие потери малы. При более низких числах Рейнольдса вязкие потери сильнее влияют на движение.
Определяется как
$$Re = {\rm{силы инерции} \over {\rm{вязкостные силы}}} = {{\rho u L}\over{\mu}} = {{u L} \over \nu} $$ 92/s$, поэтому, если произведение размера и скорости очень велико по сравнению с этим, сопротивление воздуха мало.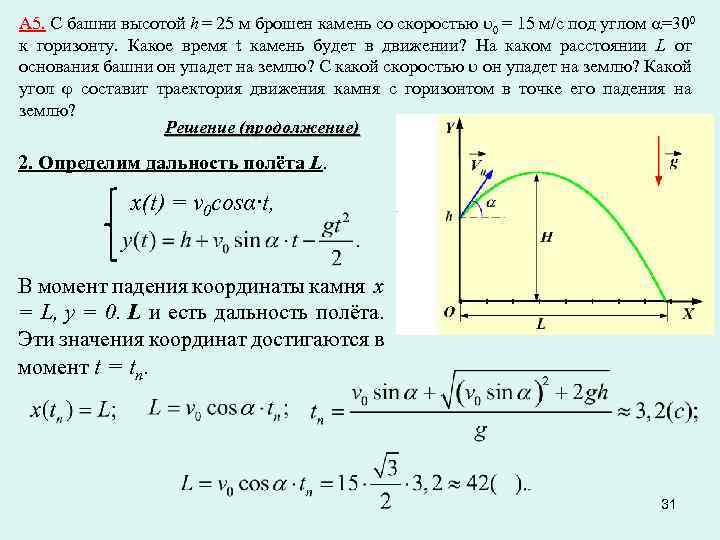
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Свободное падение и сопротивление воздуха
В предыдущем разделе было сказано, что все объекты ( вне зависимости от их массы ) свободно падают с одинаковым ускорением — 9,8 м/с/с. Это конкретное значение ускорения настолько важно в физике, что у него есть свое особое название — ускорение свободного падения — и свой особый символ — г . Но почему все объекты свободно падают с одинаковым ускорением независимо от их массы? Это потому, что они все весят одинаково? … потому что они все имеют ту же гравитацию, что и ? …потому что сопротивление воздуха у всех одинаковое? Почему? Эти вопросы будут рассмотрены в этом разделе урока 3.
В дополнение к исследованию свободного падения также будет проанализировано движение объектов, встречающих сопротивление воздуха. В частности, будут изучены два вопроса:
- Почему объекты, встречающие сопротивление воздуха, в конце концов достигают предельной скорости?
- Почему в ситуациях, когда есть сопротивление воздуха, более массивные предметы падают быстрее, чем менее массивные?
Чтобы ответить на поставленные выше вопросы, второй закон движения Ньютона (F net = m•a) будет применяться для анализа движения тел, падающих под действием единственной силы тяжести (свободное падение) и под двойным влиянием силы тяжести и сопротивления воздуха.
Как вы узнали из предыдущего раздела, свободное падение — это особый тип движения, при котором единственной силой, действующей на объект, является гравитация. Объекты, о которых говорят, что они подвергаются свободное падение , не встречающие значительной силы сопротивления воздуха; они падают только под действием силы тяжести. В таких условиях все объекты будут падать с одинаковым ускорением независимо от их массы. Но почему? Рассмотрим свободное падение 1000-килограммового слоненка и 1-килограммовой мыши-переростка.
Если применить второй закон Ньютона к их падению и построить диаграмму свободного тела, то можно увидеть, что 1000-килограммовый слоненок будет испытывать большую силу тяжести. Эта большая сила тяжести будет иметь прямое влияние на ускорение слона; таким образом, основываясь только на силе, он может показаться , что 1000-килограммовый слоненок разгоняется быстрее. Но ускорение зависит от двух факторов: силы и массы. 1000-килограммовый слоненок явно имеет большую массу (или инерцию). Эта увеличенная масса оказывает обратное влияние на ускорение слона. Таким образом, прямое воздействие большей силы на 1000-килограммового слона равно компенсируется обратным действием большей массы 1000-килограммового слона; и поэтому каждый объект ускоряется с одинаковой скоростью — примерно 10 м/с/с. Отношение силы к массе (F net /m) одинакова для слона и мыши в условиях свободного падения.
Но ускорение зависит от двух факторов: силы и массы. 1000-килограммовый слоненок явно имеет большую массу (или инерцию). Эта увеличенная масса оказывает обратное влияние на ускорение слона. Таким образом, прямое воздействие большей силы на 1000-килограммового слона равно компенсируется обратным действием большей массы 1000-килограммового слона; и поэтому каждый объект ускоряется с одинаковой скоростью — примерно 10 м/с/с. Отношение силы к массе (F net /m) одинакова для слона и мыши в условиях свободного падения.
Это отношение (F нетто /м) иногда называют силой гравитационного поля и выражается как 9,8 Н/кг (для местоположения на поверхности Земли). Сила гравитационного поля является свойством местоположения в гравитационном поле Земли, а не свойством слоненка или мыши. Все объекты, расположенные на поверхности Земли, будут испытывать такую силу (9.8 Н) на каждый 1 кг массы объекта. Будучи свойством местоположения в гравитационном поле Земли, а не свойством самого свободно падающего объекта, все объекты на поверхности Земли будут испытывать такое количество силы на единицу массы.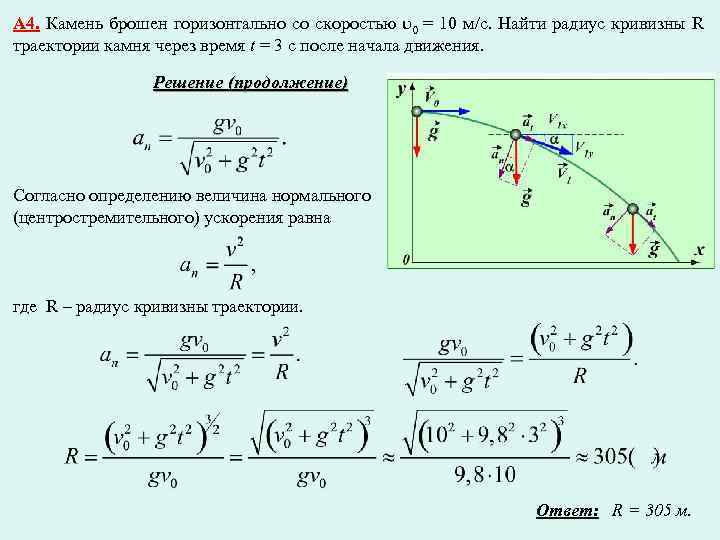 Таким образом, все объекты свободно падают с одинаковой скоростью независимо от их массы. Поскольку гравитационное поле 9,8 Н/кг на поверхности Земли вызывает ускорение любого объекта, помещенного на нее, на 9,8 м/с/с, мы часто называем это соотношение ускорением свободного падения. (Гравитационные силы будут обсуждаться более подробно в одном из следующих разделов учебника «Класс физики».)
Таким образом, все объекты свободно падают с одинаковой скоростью независимо от их массы. Поскольку гравитационное поле 9,8 Н/кг на поверхности Земли вызывает ускорение любого объекта, помещенного на нее, на 9,8 м/с/с, мы часто называем это соотношение ускорением свободного падения. (Гравитационные силы будут обсуждаться более подробно в одном из следующих разделов учебника «Класс физики».)
Посмотри!
Величина напряженности гравитационного поля ( г ) различна в разных гравитационных средах. Используйте Значение g виджета ниже, чтобы узнать силу гравитационного поля на других планетах. Выберите местоположение из выпадающего меню; затем нажмите Кнопка отправки .
Расследуй! Даже на поверхности Земли существуют локальные вариации значения g. Эти вариации обусловлены широтой (Земля не идеальная сфера, она имеет выпуклость посередине), высотой и местной геологической структурой региона. Используйте виджет Gravitational Fields ниже, чтобы исследовать, как местоположение влияет на значение g.
Эти вариации обусловлены широтой (Земля не идеальная сфера, она имеет выпуклость посередине), высотой и местной геологической структурой региона. Используйте виджет Gravitational Fields ниже, чтобы исследовать, как местоположение влияет на значение g.
Падение с сопротивлением воздуха
Когда объект падает в воздухе, он обычно сталкивается с некоторым сопротивлением воздуха. Сопротивление воздуха возникает в результате столкновений передней поверхности объекта с молекулами воздуха. Фактическая величина сопротивления воздуха, с которым сталкивается объект, зависит от множества факторов. Чтобы не усложнять тему, можно сказать, что двумя наиболее распространенными факторами, оказывающими прямое влияние на величину сопротивления воздуха, являются скорость объекта и площадь поперечного сечения объекта . Увеличение скорости приводит к увеличению сопротивления воздуха. Увеличение площади поперечного сечения приводит к увеличению сопротивления воздуха.
Увеличение площади поперечного сечения приводит к увеличению сопротивления воздуха.
Почему объект, встречающий сопротивление воздуха, в конце концов достигает предельной скорости? Чтобы ответить на эти вопросы, применим второй закон Ньютона к движению падающего парашютиста.
На приведенных ниже диаграммах показаны диаграммы свободного тела, показывающие силы, действующие на 85-килограммового парашютиста (включая снаряжение). Для каждого случая используйте диаграммы, чтобы определить результирующую силу и ускорение парашютиста в каждый момент времени. Затем используйте кнопку для просмотра ответов.
Приведенные выше диаграммы иллюстрируют ключевой принцип. Когда объект падает, он набирает скорость. Увеличение скорости приводит к увеличению величины сопротивления воздуха.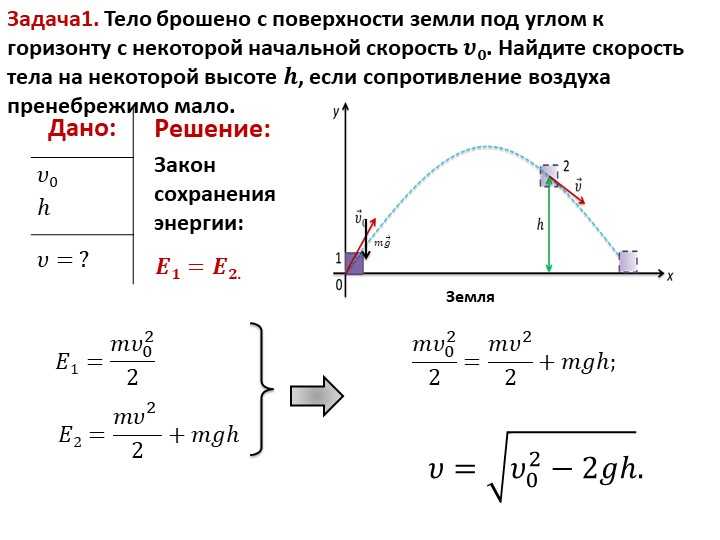 В конце концов, сила сопротивления воздуха становится достаточно большой, чтобы уравновесить силу тяжести. В этот момент времени результирующая сила равна 0 ньютонов; объект перестанет ускоряться. Говорят, что объект достиг конечной скорости . Изменение скорости прекращается в результате баланса сил. Скорость, при которой это происходит, называется конечной скоростью.
В конце концов, сила сопротивления воздуха становится достаточно большой, чтобы уравновесить силу тяжести. В этот момент времени результирующая сила равна 0 ньютонов; объект перестанет ускоряться. Говорят, что объект достиг конечной скорости . Изменение скорости прекращается в результате баланса сил. Скорость, при которой это происходит, называется конечной скоростью.
В ситуациях, когда есть сопротивление воздуха, более массивные предметы падают быстрее, чем менее массивные. Но почему? Чтобы ответить на вопрос почему , необходимо рассмотреть диаграммы свободного тела для объектов разной массы. Рассмотрим падение двух парашютистов: одного массой 100 кг (парашютист плюс парашют), а другого — 150 кг (парашютист плюс парашют). Диаграммы свободного тела показаны ниже для момента времени, когда они достигли предельной скорости.
Как было сказано выше, величина сопротивления воздуха зависит от скорости объекта. Падающий объект будет продолжать ускоряться до более высоких скоростей, пока не встретит сопротивление воздуха, равное его весу. Поскольку парашютист весом 150 кг весит больше (испытывает большую силу тяжести), он будет разгоняться до более высоких скоростей, прежде чем достигнет конечной скорости. Таким образом, более массивные объекты падают быстрее, чем менее массивные объекты, потому что на них действует большая сила тяжести; по этой причине они разгоняются до более высоких скоростей, пока сила сопротивления воздуха не сравняется с силой тяжести.
Падающий объект будет продолжать ускоряться до более высоких скоростей, пока не встретит сопротивление воздуха, равное его весу. Поскольку парашютист весом 150 кг весит больше (испытывает большую силу тяжести), он будет разгоняться до более высоких скоростей, прежде чем достигнет конечной скорости. Таким образом, более массивные объекты падают быстрее, чем менее массивные объекты, потому что на них действует большая сила тяжести; по этой причине они разгоняются до более высоких скоростей, пока сила сопротивления воздуха не сравняется с силой тяжести.
Расследуй!
Величина сопротивления воздуха, которое испытывает объект, зависит от его скорости, площади поперечного сечения, формы и плотности воздуха. Плотность воздуха зависит от высоты над уровнем моря, температуры и влажности. Тем не менее, 1,29 кг/м 3 — вполне разумное значение. Форма объекта влияет на коэффициент сопротивления ( C d ).


 Через какое время t с момента бросания первого тела они окажутся на одинаковой высоте? Сопротивлением воздуха пренебречь.
Через какое время t с момента бросания первого тела они окажутся на одинаковой высоте? Сопротивлением воздуха пренебречь. Положить g = 10 м/с2. Сопротивлением воздуха пренебречь.
Положить g = 10 м/с2. Сопротивлением воздуха пренебречь. Сопротивлением воздуха пренебречь.
Сопротивлением воздуха пренебречь.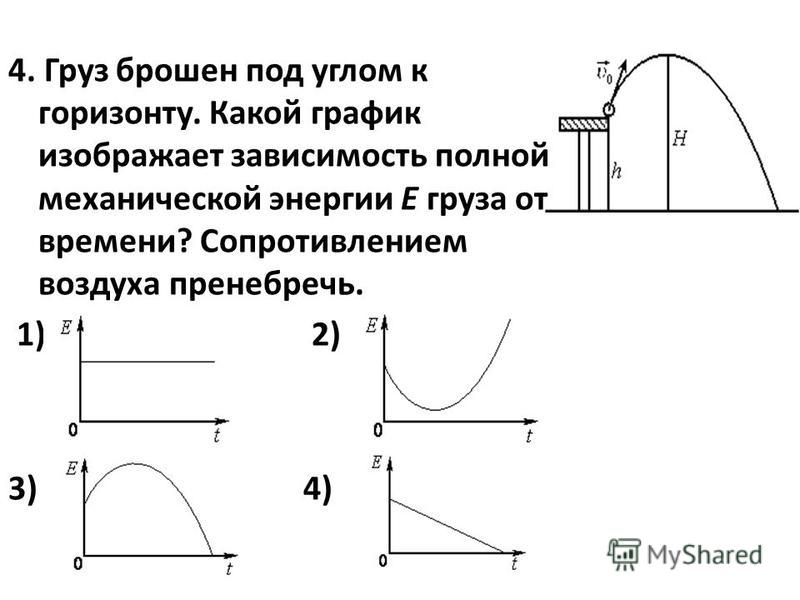 Определить кинетическую энергию Т, которую имело тело в момент удара о землю. Сопротивлением воздуха пренебречь.
Определить кинетическую энергию Т, которую имело тело в момент удара о землю. Сопротивлением воздуха пренебречь.
 Определить массу балласта, который следует сбросить за борт, чтобы аэростат получил такое же ускорение, но направленное вверх. Сопротивлением воздуха пренебречь.
Определить массу балласта, который следует сбросить за борт, чтобы аэростат получил такое же ускорение, но направленное вверх. Сопротивлением воздуха пренебречь.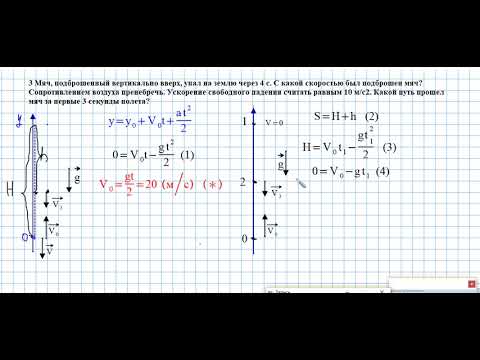 На каком расстоянии по горизонтали от точки сбрасывания груза должен находиться корабль, чтобы груз упал на палубу корабля, если пренебречь сопротивлением воздуха?
На каком расстоянии по горизонтали от точки сбрасывания груза должен находиться корабль, чтобы груз упал на палубу корабля, если пренебречь сопротивлением воздуха?
 Пренебрегая сопротивлением воздуха, найдите, сколько времени пройдет, пока камень не ударится о землю. С какой скоростью он двигается перед ударом?
Пренебрегая сопротивлением воздуха, найдите, сколько времени пройдет, пока камень не ударится о землю. С какой скоростью он двигается перед ударом? Плоскость кольца все время горизонтальна. Найдите массу кольца, если модуль индукции В магнитного поля изменяется с высотой Н по закону |В| = В0(1+αН). Сопротивлением воздуха пренебречь.
Плоскость кольца все время горизонтальна. Найдите массу кольца, если модуль индукции В магнитного поля изменяется с высотой Н по закону |В| = В0(1+αН). Сопротивлением воздуха пренебречь.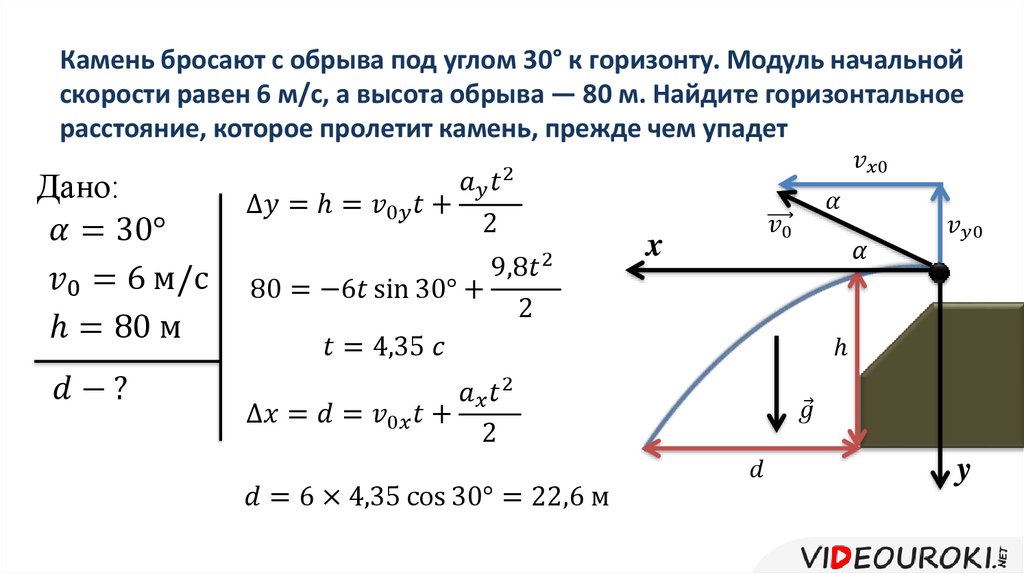 В какую сторону отклонится пуля от центра мишени? Определить расстояние между ружьем и мишенью, если боковое смещение пули от ее центра равно 1 см. Считать что пуля летит горизонтально, а ее скорость при выстреле V0 = 300 м/с. Сопротивлением воздуха пренебречь.
В какую сторону отклонится пуля от центра мишени? Определить расстояние между ружьем и мишенью, если боковое смещение пули от ее центра равно 1 см. Считать что пуля летит горизонтально, а ее скорость при выстреле V0 = 300 м/с. Сопротивлением воздуха пренебречь.

Leave A Comment